Riemann İntegrali vs Lebesque İntegrali

“İntegral ne işe yarar?” sorusuna verilebilecek en klasik yanıt muhtemelen “eğri altında kalan alanı bulmayı sağlar” olacaktır. Bu yazıda, çok da derinlere inmeden, Riemann ve Lebesque integrallerinden bahsedeceğiz. Öncelikle Riemann integralinin tanımına kısaca bir göz atalım. Bu sayede, Riemann integralinin yetersiz yönlerini ve halihazırda bir integral hesaplama yöntemi varken, neden bir de Lebesque integraline ihtiyaç duyulduğunu da anlamış olacağız.

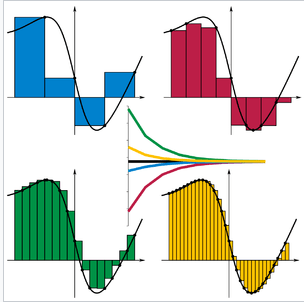
Elimizde bir $f:[a,b] \rightarrow \mathbb{R}$ fonksiyonu olsun. $y=f(x)$ eğrisinin altında kalan alanı bulmak için, $[a,b]$ aralığını n parçaya bölelim ve ilgili bölgede n adet dikdörtgen elde edelim. Daha sonra ise bu dikdörtgenlerin alanlarını toplayalım. Burada her bir dikdörtgenin kısa kenar uzunluğunun $\Delta x=\dfrac{b-a}{n}$ olduğu açıktır. Uzun kenar için ise farklı seçimler yapmak mümkündür. Eğer, aşağıdaki şeklin sol kısmında görüldüğü gibi, $f$ ‘nin bu aralıkta aldığı değerlerin infimumunu seçersek, oluşturduğumuz toplama alt toplam denir. Şeklin sağında görüldüğü gibi, o aralıkta alınan değerlerin supremumunu seçersek, bu toplama üst toplam denir.

Şimdi biz, infimum ve supremum gibi özel seçimler yapmayı bırakıp, her bir aralıktan rastgele bir ${x_i}^\ast$ noktası seçelim ve uzun kenarı $f({x_i}^\ast)$ olan dikdörtgenler oluşturalım. Oluşturulan tüm bu dikdörtgenlerin alanlarının toplamı $\sum_{i=1}^n f({x_i}^\ast)\Delta x$ olacaktır. Bu şekilde elde edilen toplamın ismi ise Riemann toplamıdır. Burada dikkat edilmesi gereken şey, dikdörtgenlerin sayısı ne kadar çok olursa, hata payının o kadar az olacağı ve alanın gerçek değerine o kadar yaklaşılmış olacağıdır.

Bunun için de yapılması gereken, $[a,b]$ ‘nin parçalanma sayısı olan n’yi sonsuza yaklaştırmaktır. İşte Riemann integrali dediğimiz şey aslında

$\int_{a}^{b} f(x) dx =\lim_{n\to \infty} \sum_{i=1}^n f({x_i}^\ast)\Delta x$

limitidir. Burada $f$ ‘yi $\mathbb{R}^2$ üzerinde bir fonksiyon olarak seçersek, integral hesabı yaparken kullandığımız yöntemi bir üst boyuta taşımamız gerekir. Bu kez tanım kümemizi belli parçalara bölüp, fonksiyonun altında kalan bölgenin dikdörtgen prizmalarından oluştuğunu ve bu prizmaların hacimlerini topladığımızı düşünebiliriz. Bundan sonra yapılacak şey ise, biraz önce kullanılan yönteme benzer şekilde, x ve y-eksenini ayırdığımız parçaların sayısını sonsuza götürmektir.

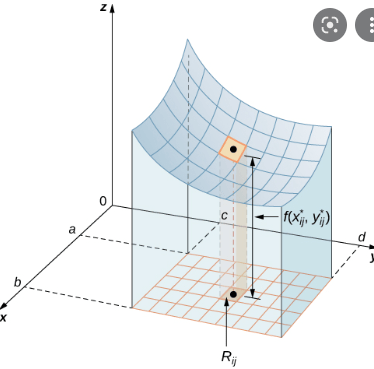
Peki $f$ ‘nin tanım kümesi herhangi bir n doğal sayısı için $\mathbb{R}^n$ ya da soyut bir $X$ uzayı olursa, bu kez nasıl bir yol izleyeceğiz? Daha geniş bir tanım kümesi ailesi için çözüm üretebilen bir integral alma yöntemimiz olsaydı fena olmaz mıydı? İşte Rieman integralinden daha genel bir integrale ihtiyaç duyulmasının sebeplerinden biri budur diyebiliriz.

Şimdi $f: [0,1]\rightarrow \mathbb{R}$ , $f(x)= \begin{cases} 1 & x\in \mathbb{Q}\cap [0,1] \\ 0 & x\in \mathbb{I}\cap [0,1] \\ \end{cases}$ biçiminde tanımlı olan Dirichlet fonksiyonunu ele alalım. $f({x_i}^\ast)$ olarak, $f$ ‘nin bu aralıktaki en büyük değeri olan 1’i alırsak, Riemann toplamı $\sum_{i=1}^n f({x_i}^\ast)\dfrac{1}{n}= \sum_{i=1}^n \dfrac{1}{n}=1$ olarak bulunur. Diğer taraftan, $f({x_i}^\ast)$ ‘nin en küçük değeri olan 0’ı kullandığımızda, Riemann toplamı $\sum_{i=1}^n f({x_i}^\ast)\dfrac{1}{n}=0$ olur. Bu iki toplam birbirinden farklı olduğundan, $f$ fonksiyonunun Riemann integrallenebilir olmadığını söyleyebiliriz. İşte Riemann integralinin diğer bir zayıf yönü de, sürekliliğe olan bağlılığıdır. Her sürekli fonksiyonun Riemann integrallenebilir olduğunu biliyoruz. Fakat karşımıza, Dirichlet fonksiyonu gibi sürekli olmayan bir fonksiyon çıktığında, bir integrallenebilme sorunu yaşamamız mümkündür. Bu problem, dikdörtgenlere ayırma işleminin imkansız göründüğü, Volterra fonksiyonu gibi patolojik fonksiyonlarda da karşımıza çıkacaktır.

Son olarak, Riemann integralinde, integral ve limit operasyonlarının sırasını kafamıza göre değiştirmenin mümkün olmadığını söyleyebiliriz. Yani bir $[a,b]$ aralığı üzerinde tanımlı, $\{{f_n}(x)\}_{n\in \mathbb{N}}$ sürekli fonksiyonlar dizisi verildiğinde

$\lim_{n\to \infty} \int_{a}^{b} f_n(x) dx = \int_{a}^{b} \lim_{n\to \infty} f_n(x) dx$

eşitliğinin sağlanması için, bu fonksiyon dizisinin düzgün yakınsak olması gerekir.

Karşılaşılan tüm bu sorunları ve Riemann integralinden daha genel bir integrale neden ihtiyaç duyulduğunu anladığımıza göre, artık Lebesque integralinin elde ediliş yöntemine geçebiliriz. Riemann integralini anlatırken, ele aldığımız fonksiyonların tanım kümelerinin değişebileceğinden bahsetmiştik. Fakat dikkat edersek, tüm bu fonksiyonların görüntü kümesi $\mathbb{R}$ oluyor, yani aslında her biri reel değerli birer fonksiyon. O halde tanım kümesini parçalara ayırmak yerine, hiçbir zaman değişmeyen görüntü kümesini parçalara ayırmak gayet mantıklı bir yaklaşım olacaktır.

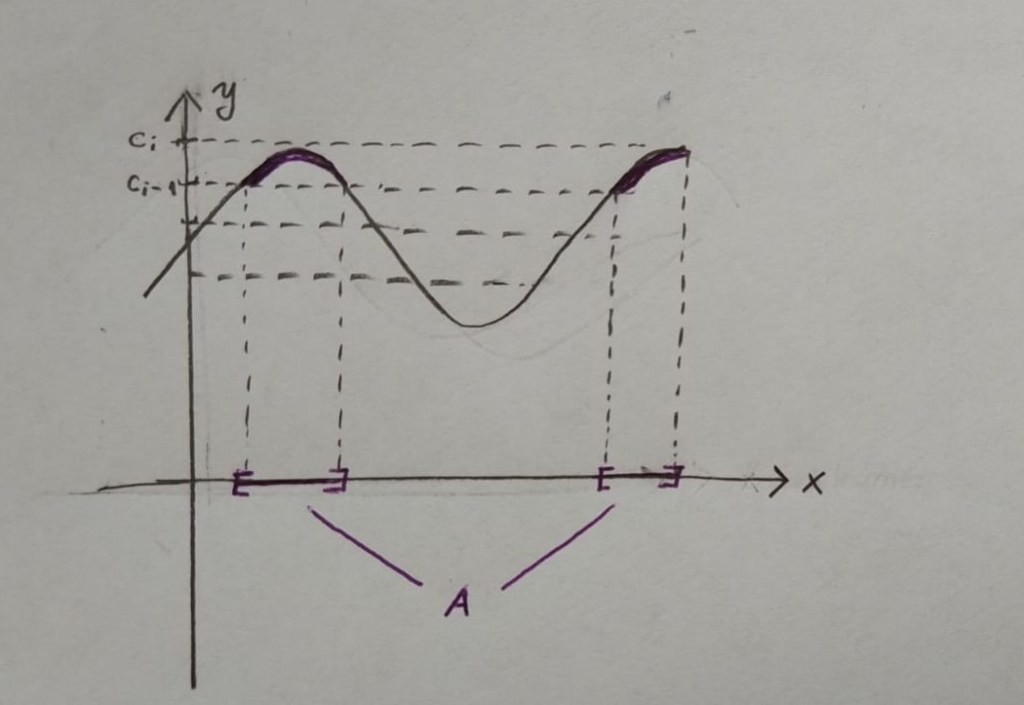
Yukarıdaki şekilde gösterilen $f(x)$ fonksiyonunu ele alalım. Burada x-ekseni $f$ ‘nin tanım kümesini temsil etsin. Yani burası sadece reel sayılar değil, herhangi bir $\mathbb{R}^n$ ya da soyut bir $X$ uzayı da olabilsin. Diğer taraftan y-ekseni $f$ ‘nin görüntü kümesini temsil ettiği için, onu reel eksen olarak ele alalım. Şimdi, y-eksenini parçalara ayıralım ve $f(x)$ fonksiyonunun her bir aralıkta ön görüntüsünü aldığımızı düşünelim. Yukarıdaki şekilde, iki aralığın birleşimi olan $A$ kümesi, fonksiyonun, $[c_{i-1}, c_i]$ aralığında kalan kısmının ön görüntüsüdür. Riemann integralini oluştururken, x-ekseni üzerinde elde ettiğimiz her bir parçanın görüntüsünü bulmuştuk ve fonksiyonumuz sürekli olduğundan, bu görüntülerin her biri bağlantılı bir küme olmuştu. Fakat görüyoruz ki, burada $A$ kümesi bağlantılı bir küme değil. Peki acaba $A$ kümesinin büyüklüğü, ya da ölçüsü nedir? Tanım kümesi $\mathbb{R}$ olsaydı uzunluğunu, $\mathbb{R}^2$ olsaydı alanını, $\mathbb{R}^3$ olsaydı hacmini ölçebilirdik. Fakat burada, birbirinden farklı her tanım kümesi için ayrı ayrı işlem yapmamak adına, genel bir ölçü tanımına ihtiyacımız olacaktır. Yani daha kapsamlı bir integral elde etmek istiyorsak, herhangi bir $X$ uzayında, kümelerin nasıl ölçülebileceğine dair bir tanımımız olması daha çok işimize yarayacaktır. Bu da bizi ölçü nedir, ölçü uzayı nasıl bir uzaydır gibi sorulara götürür. Bu kavramları daha detaylı öğrenmek isteyenler buradan devam edebilirler. Biz kabaca, ölçünün, bir $\sigma$ -cebiri üzerinde tanımlı ve belli özelliklere sahip bir dönüşüm olduğunu söyleyip yolumuza devam edelim. Elimizdeki $f$ fonksiyonun bir $\mathcal{M}$ ölçü uzayı üzerinde tanımlı olduğunu varsayalım ve bir $A$ kümesinin ölçüsünü $\mu(A)$ ile gösterelim.

$E_i=\{x : c_{i-1}\leq f(x) \leq c_i\}$ ve ${x_i}^\ast \in E_i$ herhangi bir nokta olmak üzere, genelleşmiş dikdörtgenlerin alanları toplamı $\sum_i f({x_i}^\ast)\mu(E_i)$ olacaktır. Bundan sonraki süreç tıpkı Riemann integralinde olduğu gibi işler. Örneğin $c_i$ ‘lerin seçimine göre alt ve üst toplamlar oluşur. Ekseni daha sık parçalara ayırmak ve tabii ki limit almak bizi Lebesque integralinin tanımına götürür:

$\int f(x) d\mu = \sum_i f({x_i}^\ast)\mu(E_i)$

Diyelim ki cebimizde bir miktar para var ve ne kadar olduğunu öğrenmek istiyoruz. Riemann integrali paraları cebimizden rastgele çıkarıp toplamaya benzer. Lebesque integrali ise, paraları önce türlerine göre sıralayıp (1 lira, 5 lira vs.) her birinden kaç tane olduğunu belirlemek ve her bir paranın değeri ile miktarını çarpıp daha sonra bunları toplamak gibidir.

Riemann integrallenebilir her fonksiyonun Lebesque integrallenebilir olduğunu söyleyebiliriz. Riemann integralinden daha genel olan bu integral sürekliliğe bağlı değildir, çünkü fonksiyonun süreksiz olduğu noktaların kümesini ölçmek mümkündür. Örneğin sonsuz adet süreksizlik noktası varsa ve bu noktaların kümesinin ölçüsü sıfırsa, bu durum integralimizin sonucunu etkilemez.

Bu arada, biraz önce Riemann integrallenebilir olmadığını gördüğümüz Dirichlet fonksiyonu Lebesque integrallebilirdir. Çünkü, yine kabaca anlatmak gerekirse, burada reel sayıların sayılabilir bir alt kümesi olan $\mathbb{Q}\cap [0,1]$ ‘in Lebesque ölçüsü sıfırdır. Diğer taraftan $\mu(\mathbb{I}\cap [0,1])=1$ ‘dir ve böylece $\int_{0}^{1} f(x) d\mu=1\times \mu(\mathbb{Q}\cap [0,1])+0\times \mu(\mathbb{I}\cap [0,1])=0$ olarak bulunur.

Lebesque integrali, limit ile integral operatörlerinin yer değiştirilmesi ile ilgili de güzel sonuçlar ortaya koyar. Monoton Yakınsaklık Teoremi, Baskın Yakınsaklık Teoremi ve Fatou Lemma, bu yer değişimi ile ilgili üç farklı teoremdir.

Richard W. Hamming, “Lebesgue ve Riemann integralleri arasındaki farkın fiziksel bir anlamı olabileceğine, örneğin bir uçağın uçup uçmayacağının bu farka bağlı olabileceğine inanan var mı? Böyle bir iddia varsa, o uçakta uçmak umurumda değil” diyerek, bu iki integral arasındaki farkın gündelik hayatta pek de önem arz etmediğini iddia etmiştir. Fakat Lebesque integralinin olasılık teorisi, harmonik analiz birçok farklı teoriye ve uygulamaya katkısı vardır. Bu konuyla ilgili bir savunma metnine ise buradan ulaşmak mümkündür.

Kaynaklar
1) https://www.youtube.com/watch?v=PGPZ0P1PJfw
2) https://math.berkeley.edu/~brent/files/lebesgue_integral.pdf
3) https://en.wikipedia.org/wiki/Riemann_sum
4) https://calcworkshop.com/integrals/riemann-sum/
5) T. Gowers June Barrow-Green, Imre Leader, The Princeton companion to mathematics, Princeton University Press, 2008.
6) https://www.quora.com/What-is-the-intuitive-idea-behind-Lebesgue-integration-as-opposed-to-Riemann-integration
7) https://en.wikipedia.org/wiki/%CE%A3-algebra

Topolojik bir oluşum!

Riemann İntegrali vs Lebesque İntegrali

2 thoughts on “Riemann İntegrali vs Lebesque İntegrali”

esrakorkmaz için bir cevap yazın Cevabı iptal et

Bunu paylaş:

İlgili

2 thoughts on “Riemann İntegrali vs Lebesque İntegrali”

esrakorkmaz için bir cevap yazın Cevabı iptal et