Süreklilik vs Düzgün Süreklilik

Posted on by

Süreklilik ve düzgün süreklilik, tanım olarak birbirine oldukça yakın görünen iki kavram. Peki bunları birbirinden farklı kılan o ince ayrıntı nedir. İleri analiz dersi almış olanlar tanımları arasındaki farkı mutlaka biliyorlardır. İşte şimdi bu tanımların geometrik olarak ne anlattığına bir bakalım.

Bunun için ilk olarak önce sürekliliği anlamak/hatırlamak gerekiyor. İnternette üstünkörü bir araştırma yaptığınızda, “bir fonksiyonun sürekli olması, onun grafiğini kaleminizi hiç kaldırmadan çizebilmenizdir” gibi açıklamalarla karşılaşırsınız. Bu tam olarak da doğru sayılmaz aslında. Tamam, bu şekilde çizilebilen her fonksiyon sürekli olabilir fakat her sürekli fonksiyon ille de bu özelliği sağlayacak diyemeyiz. Örneğin,

f(x)= \begin{cases} x sin {\frac{1}{x}} & x\neq 0 \\ 0 & x=0 \\ \end{cases}

parçalı fonksiyonunu elimizi kaldırmadan çizmemiz mümkün olmayacaktır. Hatta, orijinde sonsuz kez salınım yaptığından, teknik olarak, grafiği elle çizmemiz dahi mümkün olmayacaktır. Fakat bu fonksiyon reel sayılar üzerinde süreklidir.

Şimdi reel sayılar üzerinde tanımlı bir f fonksiyonun bir x_0 noktasında sürekliliğini şöyle bir oyunla anlamaya çalışalım. Karşınızdaki kişi size herhangi bir \epsilon>0 versin. y-ekseni üzerinde (f(x_0)-\epsilon, f(x_0)+\epsilon) aralığını işaretleyelim. Soru şu: Acaba (x_0-\delta, x_0+\delta) aralığındaki tüm noktaların görüntüleri (f(x_0)-\epsilon, f(x_0)+\epsilon) aralığının içinde kalacak şekilde en az bir \delta>0 sayısı bulabilir misiniz? İşte size verilen her \epsilon için bunu başarabilirseniz, fonksiyonunuz o noktada sürekli olur, yani kazanan siz olursunuz.

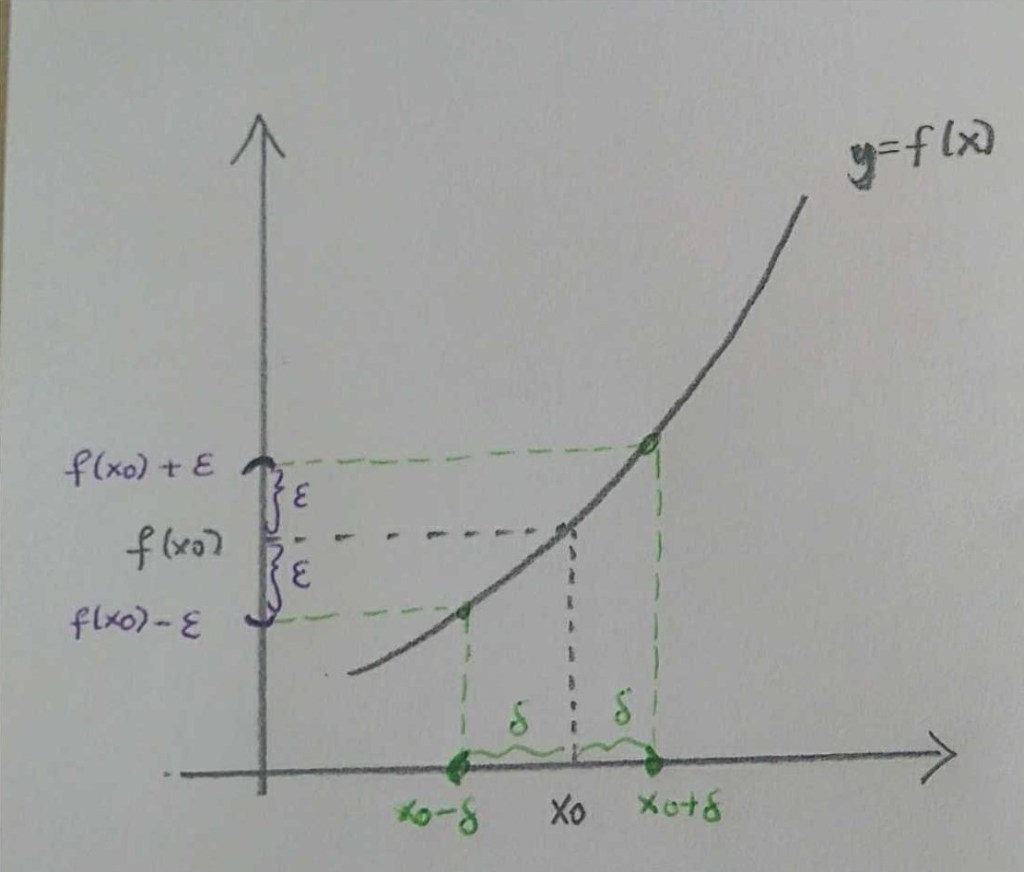
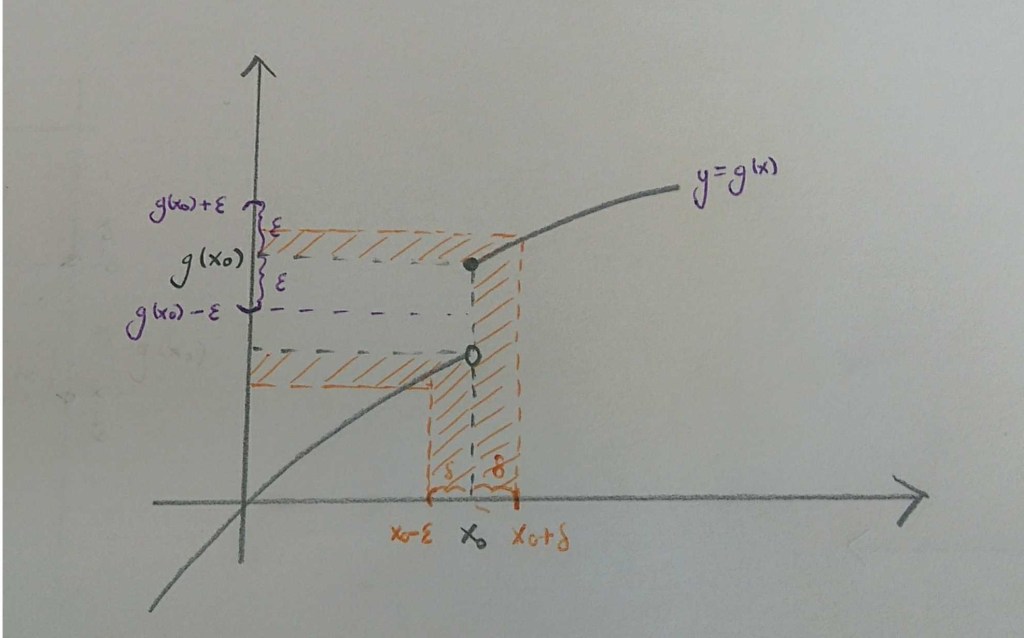
Yukarıdaki f fonksiyonunda her \epsilon>0 için başarı sağlamak mümkün. Fakat g fonksiyonu umutsuz vaka. Şekildeki gibi seçilen \epsilon sayısına karşılık, koşula uyan bir \delta maalesef bulunamaz. Çünkü ne seçersek seçelim, x_0‘ın solundaki noktaların görüntüsü bu aralığın dışına düşer.

Matematiksel olarak ifade edecek olursak,

\forall \epsilon>0, \exists \delta>0 ; (x_0-\delta<x< x_0+\delta)\Rightarrow (f(x_0)-\epsilon<f(x)< f(x_0)+\epsilon)

ya da ilk eşitsizliğin her tarafından x_0, ikincisinden ise f(x_0) çıkarırsak,

\forall \epsilon>0, \exists \delta>0 ; (-\delta<x-x_o< \delta) \Rightarrow (-\epsilon<f(x)-f(x_0)< \epsilon).

Buradan da mutlak değere geçersek,

\forall \epsilon>0, \exists \delta>0 ; \mid x-x_0 \mid < \delta \Rightarrow \mid f(x)-f(x_0)\mid <\epsilon.

(Şunu da eklemekte fayda var; burada mutlak değer yerine metrik fonksiyonu ya da komşuluklar kullandığımızda metrik ve topolojik uzaylarda süreklilik tanımını elde edebiliriz.)

Görüldüğü gibi süreklilik oldukça lokal, yani noktasal bazda bir kavram. Diyelim ki fonksiyonunuz tanım kümesindeki her noktada sürekli. Demek ki her x_0 noktasında, her \epsilon>0 sayısına karşılık en az bir \delta bulma oyununu kazanmışsınız. Fakat muhtemelen her nokta için farklı bir \delta sayısı bulmuşsunuzdur. Yani bulduğunuz \delta, hem \epsilon‘a hem de x_0 noktasına bağlıdır. İşte her nokta için ayrı bir \delta bulmak yerine her bir nokta için iş görebilecek ortak bir \delta bulunabiliyorsa bunun ismi düzgün süreklilik olur. Burada oyunu kazanmak biraz daha zorlaşıyor çünkü her kapıyı açacak bir anahtar bulmaya çalışıyorsunuz. Bunun doğal bir sonucu her düzgün sürekli fonksiyonun sürekli olması fakat tersinin her zaman doğru olmamasıdır.

Sürekli fonksiyonların grafiklerinden farklı olarak, düzgün sürekli fonksiyonların grafiklerinde ani bir artış ya da azalma olmaz. Yani grafiğin yalnızca sürekli bir fonksiyon görüntüsüne sahip olması yetmez, ayrıca çok dik de olmamalıdır.

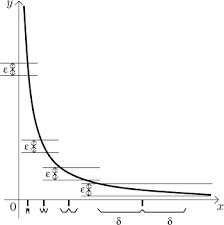
Yukarıdaki şekilde görülen f(x)=\frac{1}{x} fonksiyonunun grafiğine bakalım. Bu fonksiyon (0,\infty) aralığında sürekli olmasına rağmen düzgün sürekli değildir. Öncelikle grafiğin ne kadar dik olduğuna dikkat edelim. Şekildeki gibi seçilen bir \epsilon için bulunan \delta sayıları sola doğru gidildikçe küçüldüğünden, seçilebilecek ortak \delta sayısını sürekli daha da küçültmemiz gerekir. Bu işlem sonsuza kadar süreceği için ortak bir \delta bulmak mümkün olmaz. Sezgisel olarak da oldukça ani azalış gösteren böyle bir fonksiyonun düzgün sürekli olması beklenmezdi.

Diğer taraftan yine aynı fonksiyon [1,\infty) aralığında düzgün süreklidir. Aralığın en sol ucundaki \epsilon‘a karşılık gelen \delta, tüm aralıkta iş görecektir.

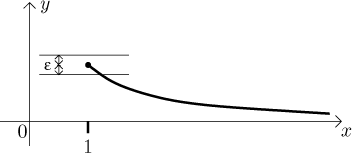
Bir tanımı, problemi mümkün olduğunca görselleştirmek bizi ezberin gereksiz yükünden ve anlaşılmazlığından kurtarır. Yukarıda anlatılanlar düzgün süreklilik ile ilgili teoremleri ve kuralları da daha kolay yorumlamamıza yardımcı olacaktır.

KAYNAKLAR
1) https://math.fel.cvut.cz/mt/txtb/3/txe3ba3g.htm

4 thoughts on “Süreklilik vs Düzgün Süreklilik”

  2. anlattığınız için teşekkürler. Sadece aklıma bir şey takıldı. Son görselde (fonksiyonda) her epsilona uyan delta ne acaba. keşke öbür epsilonlar ve verdiğiniz epsilon için deltayı da verseydiniz. o konuda bir tık kafam karıştı

    Beğen

    Reply ↓

    • Kafa karıştırıcı olur diye sayısal veriden kaçmıştım ama haklısınız, bu haliyle biraz üstü kapalı olmuş sanki.
      Burada önce (0, sonsuz) aralığını, (1,sonsuz) aralığından ayıran şeyden bahsetmek mantıklı olacaktır. Diyelim ki \epsilon=0.1 olsun. x=1 ve y=1.01 noktalarını seçelim. Bu durumda |f(x)-f(y)| yaklaşık olarak 0.0099 oluyor ve açıkça, epsilondan oldukça küçük. Şimdi sıkıntılı bölge olan (0,1) aralığından iki noktayla bir deneme yapalım. x=0.10, y=0.11 olsun. Bu durumda, |f(x)-f(y)| yaklaşık 0.9091 oluyor. Epsilondan küçük olmasını geçtim, korkunç bir artış gerçekleşti. Dikkat ederseniz seçtiğim her iki nokta çifti arasındaki mesafe eşit, yani \delta=0.01 idi. f(x) ve f(y) arasındaki mesafenin hala epsilondan küçük kalması için deltayı küçültme kararı alsam, bu kez grafikte sola kaydığımda kuralı ihlal eden bazı x, y çiftleri ile mutlaka karşılaşırım. Yani, 0’a yaklaştıkça 1/x hesabından dolayı korkunç bir büyüme gerçekleşiyor ve ortak bir delta elde etmek adına sürekli küçülmeye gitmek zorunda kalıyorum ve haliyle bunun da bir sonu yok.
      Son görselde durum farklı. (0,1) aralığına girmiyorum, artışlar korkunç bir hal almıyor. Burada her epsilon için, \delta=\epsilon seçmek yeterli olacaktır. Onu da ancak ispat yoluyla gösterebilirim.
      Keyfi ve adı koyulmamış bir epsilon seçelim. Her x, y için |x-y|<\delta olduğunda; |f(x)-f(y)|=|1/x-1/y|=|y-x|/xy < |y-x| < \delta olduğundan, \delta=\epsilon olarak seçersem, |x-y|<\delta iken |f(x)-f(y)|<\epsilon elde etmiş olurum. (Son kısımda 2 bilgi kullandım: 1) |y-x|=|x-y|1 ve y>1, yani dolayısıyla xy>1. Bu nedenle |y-x|/xy 1 ve y>1 bilgisi ile bir sonraki adıma geçebildim. (0,sonsuz) aralığında, buna engel olan şey tam olarak da bu bilginin kesin olmaması.

      Umarım açıklayıcı ve faydalı olmuştur.

      Beğen

      Reply ↓

Huri Melek için bir cevap yazın Cevabı iptal et