sonsuz küçük | Topolojik bir oluşum!

$\Delta x=x-x_0$ , $x$ -koordinatındaki, $\Delta y=y-y_0$ ise $y$ -koordinatındaki değişimi göstermek üzere, bir doğrunun eğiminin $\frac{\Delta y}{\Delta x}= \frac{y-y_0}{x-x_0}$ olduğunu biliyoruz. Peki bir eğrinin eğimi ile neyi kastediyoruz? Yani örneğin $y=x^2$ parabolünün belli bir noktada eğimini bulmak ne anlama gelir? İşte bunu anlamak için önce sonsuz küçüklerin dünyasına bir giriş yapmamız gerekir.

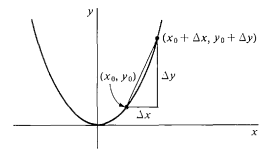
$P=(x_0,y_0)$ ve $Q=(x_0+\Delta x, y_0+\Delta y)$ bu eğri üzerinde alınmış iki farklı nokta olmak üzere, eğrinin bu noktalar arasındaki ortalama eğimi (ya da değişimi) $\frac{\Delta y}{\Delta x}$ ‘dir. Yani aslında bu iki noktadan geçen doğrunun eğimine eşittir. Şimdi Pisagor teoreminden bu eğimin neye eşit olduğunu bulalım.

Öncelikle $P$ ve $Q$ noktaları bu eğri üzerinde olduğundan, $y_0={x_0}^2$ ve $y_0+\Delta y=({x_0+\Delta x})^2$ eşitliklerinin sağlandığını söyleyebiliriz. Burada 2.eşitliği 1. ‘den taraf tarafa çıkarırsak,

$y_0+\Delta y-y_0=\Delta y=({x_0+\Delta x})^2-{x_0}^2=2 x_0 \Delta x+(\Delta x)^2$

elde ederiz. Bu durumda ortalama eğim $\frac{\Delta y}{\Delta x}=\frac{2 x_0 \Delta x+(\Delta x)^2}{\Delta x}=2 x_0 + \Delta x$ olur. Burada son eşitliği yazmak, yani $\Delta x$ ‘leri sadeleştirebilmek için, $\Delta x\neq 0$ koşulunun sağlanması gerektiğine dikkat edelim. Çünkü aksi halde $\frac{0}{0}$ belirsizliği ile karşılaşırız.

Peki acaba $P=(x_0, y_0)$ noktasındaki eğimi nasıl bulabiliriz? Tamam, $\Delta x$ yine 0’dan farklı olsun, ama 0’a da çok yakın olsun. Yani o kadar küçük olsun ki, $Q$ noktası $P$ noktasının iyice yakınında bulunsun. İşte bu durumda, 0’a çok yakın olan bu $\Delta x$ sayısını ihmal ederek, $P$ noktasındaki eğimin $2 x_0$ değerine oldukça yakın olacağını söyleyebiliriz. Bu durumda örneğin $(2,4)$ noktasındaki eğim yaklaşık olarak 4’e eşit olacaktır.

Burada asıl sorun bu “ihmal etme” işini neye göre yaptığımız. Yani hangi sayılar ihmal edilecek kadar küçük, hangileri değildir? İşte bir matematikçi olarak bize düşen, her zaman yaptığımız gibi, buna bir standart getirmek ve bir tanım yapmaktır.

Eğer her $a\in \mathbb{R}$ için $-a<\epsilon <a$ oluyorsa, bu $\epsilon$ sayısına sonsuz küçük (infinitely small, infinitesimal) denir.

Burada, sonsuz küçüklerin birer reel sayı değil, her pozitif reel sayıdan daha küçük olan yeni bir sayı türü olduklarına dikkat edelim. Farklı isimlerle de olsa, sonsuz küçük kavramının kullanımı çok eskilere dayanır. Arşimet ve hatta ondan yaklaşık iki asır önce Eudoxus, eğrilerle sınırlı bir bölgenin alanını bulmak için, bu bölgeyi, alanı bilinen küçük ve oldukça fazla bölgeyle doldurma yöntemini kullanmışlardır. Hatta ileri Analiz derslerinden tanıdık gelecek ve bir sonraki yazıda bahsedeceğimiz Arşimet (Archimedean) özelliği de aslında yine sonsuz küçüklerle ilgilidir. Bu özelliği sağlayan (örneğin reel sayılar gibi) bir sistemde sonsuz küçükler yoktur.

17. yüzyılda büyük gökbilimci Johannes Kepler, ikinci düğünü için malzeme satın alırken, tüccarların şarap fıçısının içindeki şarap miktarını belirlemek için kullandıkları yanlış yöntemlerden memnun kalmamıştır. Bunun üzerine, konik kesitlerin bazı eksenler etrafında döndürülmesiyle elde edilen yaklaşık 100 dönel cismin hacmini bulmaya çalışmıştır.

Kepler, hacim hesabı yapmak için sonsuz küçük geometrik nicelikler kullanmıştır. Örneğin, şarap fıçısının her biri silindir olan tabakalardan oluştuğunu düşünmüş ve hacmini hesaplamak için bu tabakaların hacimlerini toplamıştır.

Kepler’in bu buluşu ışığında, İtalyan matematikçi Bonaventura Cavalieri, 1635 yılında alanları ve hacimleri hesaplamak için bölünmezler (indivisibles) yöntemini ortaya koymuştur. Bölünmezler, bulunduğu cismin/şeklin bir boyut düşüğünde yaşarlar. Örneğin, bir kitabın sayfalarını iki boyutlu olarak düşünürsek, bu iki boyutlu bölünmezler yardımıyla üç boyutlu bir kitabın hacmini hesaplayabiliriz. Tıpkı günümüzde integral hesabında yaptığımız gibi.

Sonsuz küçükler, Newton ve Leibniz’in kalkülüsünde de kullanılmışlardır. Örneğin diferansiyel dediğimiz şey aslında bir değişkendeki sonsuz küçük değişimleri temsil eder. Aşağıdaki videoda, limit kullanmadan, sadece sonsuz küçükler yardımıyla $\sin(x)$ fonksiyonunun türevinin $\cos x$ olduğunun gayet güzel bir ispatı mevcut. Newton, Leibniz ve sonrasında gelen birçok kişi, kalkülüse tıpkı bu şekilde, yani sonsuz küçüklerin işin içinde olduğu sezgisel yollarla yaklaşmışlardır.

Sonsuz küçük kavramı öyle sezgiseldir ki, var olduklarını kabul etsek bile tam olarak ne oldukları hakkında bir fikir sahibi olamayız. Yani öyle bir şey ki; “Bir sayı var biliyoruz. Epiyce yaklaşıyoruz, duyuyoruz, anlatamıyoruz.” Şu an bile aklımızı böylesine zorlayan bu kavram, haliyle o zamanlar da birçok itiraza sebep olmuştur. Örneğin George Berkeley, The Analyst isimli kitabında sonsuz küçükleri “ölmüş niceliklerin hayaletleri” olarak tanımlamıştır ve ayrıca

“Ne kadar küçük olursa olsun bir şey ihmal ediliyorsa, hızın kesin bir değere değil ancak yaklaşık bir değere sahip olduğunu söyleyebiliriz. (…) Artışların yok olduğunu varsayıyorsak, artışların var olduğu yönündeki ilk varsayım terk edilmiş demektir, bu durumda o ilk varsayımın sonuçlarından biri sayesinde elde edilmiş bir sonuçla karşılaşırız, ki bu da yanlış bir akıl yürütmedir.”

diyerek tepkisini ortaya koymuştur. Fakat biliyoruz ki, tüm bu itirazlara rağmen, sonsuz küçüklere dayalı integral ve türev hesabı şuan bile geçerliliğini koruyor. Hatta Abraham Robinson sayesinde, bugün sonsuz küçükleri kullanarak da kalkülüs yapılabilineceği biliniyor. Robinson’un ortaya koyduğu ve standart olmayan (non-standart) analiz ismiyle bilinen bu sistem, tüm reel sayıları ve 0 dışındaki tüm sonsuz küçükleri içeren Hiperreel Sayılar üzerine kurulmuştur. Kalkülüsün sonsuz küçükler yardımıyla baştan sona nasıl inşa edildiğini merak edenler, H. Jerome Keisler’ın bu konuda yazılmış oldukça kapsamlı kitabına buradan ulaşabilirler. Modern analize büyük ölçüde yön vermiş olan sonsuz küçükleri anlamak, hem birçok fikrin nasıl doğduğuna şahit olmamızı sağlayacak, hem de aslında neyi ifade etmeye çalıştıklarını anlamamızı kolaylaştıracaktır.

Kaynaklar
1) M.T. Carroll, S.T. Dougherty, D.Perkins, Indivisibles, Infinitesimals and a Tale of Seventeenth-Century Mathematics, Mathematics Magazine, 86, 239–254, 2013.
2) https://people.math.wisc.edu/~keisler/calc.html
3) https://infinityisreallybig.com/2019/11/30/infinitesimal-calculus-and-calculus-rules/
4) http://amsi.org.au/ESA_Senior_Years/SeniorTopic3/3a/3a_4history_3.html
5) https://www.maa.org/press/periodicals/convergence/kepler-the-volume-of-a-wine-barrel-introduction

Topolojik bir oluşum!

Tag Archives: sonsuz küçük

Sonsuz Küçükler: “Epiyce yaklaşmışım, duyuyorum, anlatamıyorum”