Kararsız biri olduğunuzu düşünüyor ve seçim yapmakta zorlanıyor musunuz? İşte şimdi okuyacağınız yazı size gerçek hayatta, yani sonlu seçenek söz konusu olduğunda seçmenin aslında ne kadar kolay olduğunu, işin içine sonsuzluk girdiğinde ise olayların ne kadar karışacağını gösterecek. Ayrıca yine sonsuzluk durumunda seçmeye ait bir kabulün, hem ne kadar işe yaradığını hem de işleri nasıl çığırından çıkaran sonuçlara yol açtığını da görmüş olacağız.

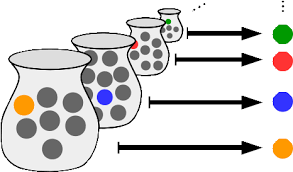
Elimizde sonlu sayıda kavanoz olduğunu varsayalım. Bu kavanozların içinde renkli toplar olsun. Her birinden birer top seçme işlemi kolaydır, çünkü sonlu sayıda adım içerir. Şimdi de her birinin içinde doğal sayılar olan sonsuz tane kümemiz olduğunu düşünelim. Doğal sayılardan oluşan bu kümelerin mutlaka en küçük elemanları vardır. (Hatırlayalım: Doğal sayılar kümesi iyi sıralıdır.) O zaman her kümeden en küçük elemanı almak gayet güzel bir seçim olacaktır.

Bahsettiğimiz seçme zorluğunun nedenini en güzel anlatan örnek Bertrand Russell’dan geliyor: Sonsuz çift ayakkabıya ve çoraba sahip birisiniz. Her çift ayakkabıdan birini seçmek istediğinizde her birinin sol tekini alabilirsiniz. Fakat iş her çift çoraptan birini seçmeye geldiğinde, çoraplar özdeş olduğundan kesin bir yanıt vermek mümkün olmayacaktır. Burada olduğu gibi, her sonsuz durum açık bir seçime izin vermez. İşte böyle durumlarda imdadımıza Seçme Aksiyomu yetişir ve boştan farklı her küme için bir seçim yapmanın mümkün olduğunu söyler. Yani durum şu ki, bir ispatın tam ortasında elimdeki şu kümelerden birer eleman seçeyim diyorsunuz. Üstelik elinizde herhangi bir kural yokken. Kimse size neyi ne şekilde seçtiğinizi sormuyor ve Seçme Aksiyomunu kullandım deyip yola devam edebiliyorsunuz.

Öklid’in 5. postulatında olduğu gibi, Seçme Aksiyomunu da ispatlamaya ya da çürütmeye çalışanlar olmuştur. Kurt Gödel, bu aksiyomun Kümeler Kuramının diğer aksiyomları ile birlikte çelişkisiz bir sistem oluşturduğunu; Paul Cohen ise diğer aksiyomlardan bağımsız olduğunu, Seçme Aksiyomunu varsayan ya da varsaymayan kuramlar olabileceğini göstermiştir. Sonuç olarak elimizde ispatlanamaz ya da doğruluğu çürütülemez böyle bir aksiyom var biz de bunu kullanarak aşağıdaki problemi çözmeye çalışabiliriz.

Önce bazılarınıza tanıdık gelecek bir zeka sorusuyla başlayalım. Arka arkaya sıralanmış 100 kişinin başına siyah ve beyaz şapkalar rastgele takılıyor. Sıradakiler önlerindekileri görebilir fakat arkalarına ve kendi şapkalarına bakmaları yasak. Bir moderatör, sıranın en arkasından başlayarak şapkalarının rengini tahmin etmelerini istiyor. Sıradakiler tahminleri duyabiliyor fakat doğruluğu/yanlışlığı hakkında bir şey bilmiyorlar. Acaba en fazla doğru cevabı elde etmek için nasıl bir yol izlenmesi gerekir? Mesela 100. kişi 99. kişinin şapka rengini söylese, 99. bunu duyarak doğru yanıt vermiş olur. Benzer şekilde çift numaralı kişiler önlerinde bulunanların rengini söylediğinde yarı yarıya bir başarı yakalamak mümkün. Fakat daha iyisi de yapılabilir.

100. kişi kendi rengini tahmin etmek yerine, önündeki tüm siyah şapkaları saysın. Siyah şapkaların sayısı çiftse beyaz, tekse siyah cevabını versin. Sıra 99. kişiye geldiğinde o da siyah şapkaları saysın. Eğer 100. kişi ile aynı veriye ulaşmıyorsa, yani örneğin 100. kişi çift bulmuşken kendisi tek buluyorsa, siyah şapka sayısı bir azalmış demektir. Bu durumda kendi şapkası siyah olmalıdır. Fakat 100. kişi ile aynı veriye ulaşmışsa, siyah şapka sayısında değişme olmamış demektir ve kendi şapkası beyazdır. 98. kişi hem 100. kişinin ne gördüğünü hem de 99. kişinin hangi renk şapka taktığını bildiğinden, siyahları sayarak kendisi için doğru bir tahminde bulunabilir. Bu şekilde ilerlersek, 100. kişi hariç herkes doğru yanıt vermiş olur ki bu oldukça başarılı bir stratejidir.

Yukarıdaki sorunun Seçme Aksiyomu ile hiçbir ilgisi yok tabii ki. Ama bu problemin sonsuz duruma uyarlanmış bir versiyonunu biraz matematik kullanarak çözebiliriz. Sonsuz sayıda insanla birlikte arka arkaya, bir sayı doğrusu üzerinde, yüzlerimiz pozitif yöne dönük olacak şekilde sıralandığımızı varsayalım. Fakat sıra her iki taraftan da sonsuz olmasın, yani sıradaki herhangi bir kişinin önünde sonsuz sayıda, arkasında ise sonlu sayıda kişi olsun. Bu kez her bir şapkanın üzerinde bir reel sayı olduğunu ve kendi şapkamızda yazılı olan sayıyı tahmin etmeye çalıştığımızı düşünelim. Hatta olayı biraz daha zorlaştırmak adına kimse arkasındaki kişinin ne söylediğini duyamasın. Seçme Aksiyomu kullanarak sadece sonlu sayıda kişinin yanlış cevap vereceği, sonsuz sayıda kişinin doğru yanıt vereceği bir senaryo oluşturmak mümkündür.

Nasıl mı? İlk olarak olası tüm tahminlerin kümesini, yani sonsuz reel sayı dizilerinden oluşan kümeyi ele alalım. İlk olarak bu küme üzerinde şöyle bir denklik bağıntısı tanımlayalım: Eğer herhangi iki dizinin yalnızca sonlu sayıda bileşeni birbirinden farklı ise bu iki dizi birbirine denk olsun. Örneğin ve dizileri bu bağıntıya göre birbirlerine denktir fakat dizisi bu iki diziye de denk değildir. Şimdi de kümemizi bu bağıntıya göre parçalayalım, yani birbirine denk olan tüm dizileri aynı küme atarak ana kümeyi bölüntülere ayıralım. Yaptığımız işlem aslında kümeyi elimizdeki denklik bağıntısına göre denklik sınıflarına ayırmaktır. Yukarıdaki örnekteki ilk iki dizi aynı kümenin elemanı iken, üçüncü dizi kendisine denk olan diğer tüm elemanlarla birlikte başka bir kümede ikamet edecektir. Bu noktada Seçme Aksiyomunu kullanarak her bir kümeden, yani denklik sınıfından, sıradaki herkesin hemfikir olacağı birer temsilci seçelim.

Ön hazırlıklar tamam. Şimdi moderatör geliyor ve sol baştan şapka numaralarını tahmin etmemizi istiyor. Sıra bana geldiğinde, arkamda bulunan sonlu sayıda kişiden haberim olmasa da, önümde bulunan sonsuz sayıda kişiye bakarım ve dizinin hangi temsilci ile denk olduğunu saptayabilirim. Sonra da, temsilci dizide kendi bulunduğum konumdaki reel sayıyı moderatöre söylerim. Tahminim doğru olmayabilir, sorun yok. Benzer işlemi önümdeki her bir kişinin de yaptığını düşünelim. Bağıntımızın özelliğinden, bir yerden sonra kişilerin şapka numaralarından oluşan dizi ile temsilci dizinin aynı şekilde devam edeceğini biliyoruz. Yani benimle birlikte sonlu sayıda kişi doğru tahminde bulunamamış olsa bile, dizilerin aynı devam ettiği o noktadan sonra her tahmin mutlaka doğru olacaktır, ki bu da sonsuz sayıda doğru cevap demektir.

Seçme Aksiyomunun kümeler teorisinden cebire, çizge teorisinden topolojiye kadar birçok alanda kullanımı mevcuttur. Tabii burada o kadar derin matematik yapmak gereksiz ama meraklıları şuraya bir göz atabilir ve şuradan da Seçme Aksiyomu yardımıyla ölçülemez bir kümenin nasıl elde edilebileceğini izleyebilirler.

Son olarak Seçme Aksiyomunun nasıl bir paradoksa yol açtığına bakalım. 1924 yılında Polonyalı matematikçiler Stefan Banach ve Alfred Tarski tarafından ispatlanan akıllara zarar Banach-Tarski Paradoksu bize, Seçme Aksiyomunun doğruluğunu kabul etmemiz halinde şöyle çılgın bir sonuca ulaşabileceğimizi söylüyor: İçi dolu bir top alalım ve bu topu sonlu sayıda parçaya bölelim. (Parçalardan biri sadece merkezi içeren tek nokta kümesi olmak üzere 5 parça bu iş için yeterli.) Teoreme göre bu parçaları birleştirerek ilk top ile özdeş iki adet top yapmak mümkün. Üstelik parçaları esnetmek, eğip bükmek gibi hilelere gerek olmadan.

Tabii bu teoremin fiziksel nesneler için değil, yalnızca matematiksel nesneler için geçerli olduğunu belirtmekte fayda var. Derin ispata girmek istemeyen genel okuyucu kitlesi için şurada gayet güzel bir açıklama mevcut. Grup teori severler ise teoremin ispatına buradan ulaşabilirler.

Bu olumsuz sonuca rağmen yapmamız gereken, Dr Strangechoice‘un da dediği gibi, Seçme Aksiyomu hakkında endişelenmeyi bırakıp onu sevmeyi öğrenmek. Evren, Seçme Aksiyomu olmadan çok garip bir yer olabilir çünkü bu durumda bir kümeyi ayrık, boş olmayan parçalara böldüğümüzde, parça sayısının bölünen kümenin eleman sayısını geçmesi gibi tuhaf sonuçlarla karşılaşabiliriz.

KAYNAKLAR
1) https://jaydaigle.net/blog/what-is-the-axiom-of-choice/
2)https://acikders.tuba.gov.tr/pluginfile.php/579/mod_resource/content/0/hafta_21_22.pdf
3)https://www.irregularwebcomic.net/2339.html