Bir oyun oynuyoruz ve topolojinin ilerlemesine katkıda bulunuyoruz. Oyunumuzun ismi Nice Neighbors.

Chris Staecker tarafından tasarlanmış olan bu oyun, yukarıda gördüğünüz gibi dairelerin içinde bulunan bazı noktalar ve bunları birleştiren çizgilerden oluşuyor. Yapmanız gereken, mavi noktaları birbirlerinin üstüne taşımak (dikkat edelim: dairelerle birlikte değil, sadece noktaları taşımak) ama tabii öyle rastgele değil. İşte kurallar: Noktaları yalnızca onlara bitişik olan bir noktaya taşıyabilirsiniz, yani noktalar evlerinden yalnızca bir nokta kadar uzağa gidebilirler. Ayrıca bunu yaparken tüm çizgilerin mavi kalmasına dikkat etmeniz gerekiyor. Kırmızı bir çizgi ile karşılaşıyorsanız yanlış bir hamle yapıyorsunuz demektir. Kazanmak için oyun sonunda ez az bir dairenin boş kalması ve tüm çizgilerin mavi olması gerekiyor.

Hemen denemek isteyenleri buraya alalım ve oyunun altında yatan matematiksel gerçekleri ve Staecker’ın oyunu tasarlama amacını anlamaya çalışalım.

Öncelikle oyun dijital topoloji ile ilişkili olduğundan, burada anlatılan bazı kavramlara ihtiyacımız olacak. Bu nedenle kısaca bir göz gezdirmekte fayda var.

bir dijital görüntü olsun. Eğer aşağıdaki özelliklere sahip bir fonksiyonu varsa indirgenebilirdir (reducible) denir:

(a) örten değildir.
(b) Her pikseli için ile bitişiktir.
(c) Eğer ve bitişik ise ve de bitişiktir.

Böyle bir fonksiyonu yoksa, görüntüsü indirgenemezdir (irreducible) denir.

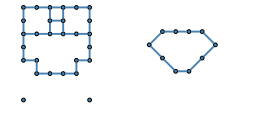
Yukarıda verilen iki dijital görüntüyü ele alalım. (Soldaki görüntüde 4-bitişiklik, sağdakinde ise 8-bitişiklik kullanıldığına dikkat edelim.) Olası tüm indirgemeler yapıldığında, son halleri aşağıdaki iki indirgenemez görüntü olacaktır. Bunu yaparken görüntünün topolojisinin değişmediğine, yani delikler (holes) ve bağlantılılık (connectivity) ile ilgili özelliklerinin aynı kaldığına dikkat edelim.

Eğer ‘yi, Nice Neighbors oyunundaki gibi, bir çizgenin köşelerini yeniden düzenleyen bir dönüşüm olarak düşünürsek, yukarıdaki koşulların şu anlama geldiğini görebiliriz:

(a’) Yapacağınız hamle sonrasında en az bir köşe noktası boş kalmalıdır.
(b’) Her nokta sadece bitişiği olan bir noktaya taşınabilir.
(c’) İki bitişik köşe, yaptığınız hamle sonrasında da bitişik olarak kalmalıdır.

Staecker ve öğrencileri hangi çizgelerin indirgenebilir, hangilerinin indirgenemez olduğu sorusuna yanıt bulmak istiyorlardı. Bunu yaparken, “verilen bir çizgenin bir dijital görüntünün çizgeleştirilmiş hali olup olmadığı” açık sorusuna hiç bulaşmamak için tüm çizgeleri ele alma yolunu seçmişlerdi. İşte oyunun tasarlanma amacı da buydu. (İlham kaynağının, John Tantalo’nun, amacı bir çizgeyi düzlemsel hale getirmek olan Planarity oyunu olduğunu belirtmekte fayda var.) Nice Neighbors’da kazanılan her çizge, o çizgenin indirgenebilir olduğunun ispatıdır. (a’) ve (b’) özellikleri zaten oyunun kuralları arasındadır. Hata yaptığınızı gösteren kırmızı çizgi ise aslında (c’) özelliğinin sağlandığını garanti eder. Nasıl mı?

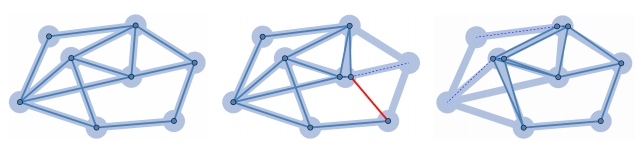
Soldaki çizge ile işe başladığımızı varsayalım. Ortadaki çizgedeki kırmızı çizgi, aslında bitişik olması gereken iki noktanın, yaptığımız hamle sonrasında bitişik olmayacağı konusunda bir uyarıdır. Yani bu hamleyi yaparsak (c’) koşulu sağlanmamış olur. Fakat en sağdaki çizge, her 3 koşulu da sağladığından soldaki çizgenin indirgenmiş halidir.

Oyun oldukça işe yaramış ki, 2 ay içerisinde 9 noktaya kadar olan indirgenemez grafiklerin bir listesini çıkarmayı başarmışlar.

“İyi matematik sadece cevapları bulmakla değil, onları açıklamakla da ilgilenir. Cevapları bulmuş olmak benim için tatmin edici, ancak bu cevapların neden doğru olduğunu hala anlamadığım hissinden kurtulamıyorum. Umarım birileri bir gün her şeyi çözer.“

diyor Staecker. İşte bu da, bu konular üzerinde çalışmaya hevesli olanlar için bir çağrı niteliğinde olsun.

Kaynaklar
1) P. Christopher Staecker, Nice Neighbors: A Brief Adventure in Mathematical Gamification, Math Horizons 23(4), 5-7, 2016.