Telefonunuzu çıkarıp en yakın kahve dükkanını her aradığınızda, farkında olmadan matematiğin en zarif uygulamalarından birine tanık oluyorsunuz. Haritalar uygulamanızı açtığınızda, ekranınızda beliren o mavi nokta aslında bir sihir değil, sadece hareket halindeki matematik. Size nerede durduğunuzu söyleyebilmek için gerçek zamanlı olarak binlerce denklemi çözüyor. Başınızın kilometrelerce üzerinde, hassas mühendislikle üretilmiş uydularda atomik saatler çalışıyor ve her biri atmosfer boyunca sinyaller yayıyor. Akıllı telefonunuz uzaydan gelen bu fısıltıları yakalıyor ve bu bilgiyi, dünya üzerindeki konumunuza dönüştürüyor. Tüm bu kozmik orkestranın şefi ise “Doğrusal Cebir”.
GPS günümüzde elektrik veya su gibi sıradan bir hizmet olarak görülüyor. Ancak bu basit ara yüzün altında, eski çağlardaki denizcileri hayrete düşürecek matematiksel bir harika yatıyor. Onlar usturlab ve yıldızlara güvenirken, biz konumumuzu hassasiyetle belirlemek için doğrusal denklemleri, matris dönüşümlerini ve özdeğerleri (eigenvalues) kullanıyoruz. Bu yazıda, uydular yardımıyla mesafe ölçmek gibi temel bir fikrin, doğrusal cebirle çözülebilecek bir probleme nasıl dönüştüğünü inceleyeceğiz.
Günümüz GPS alıcıları birçok farklı konumlandırma tekniği kullanır. Her tekniğin matematiği biraz farklı olsa da, hepsinin temelinde trilaterasyon yöntemi yatar. Trilaterasyon, koordinatları bilinen noktalardan, uzaklıkları ölçerek konum belirleme yöntemidir. Bunu günlük hayattan bir örnekle açıklayalım:
Bir şehirde kaybolduğumuzu ve üç farklı kişiye, onlardan ne kadar uzakta olduğumuzu sorduğumuzu düşünelim. A, B ve C kişileri bize, onlardan sırasıyla 3, 4 ve 3.5 metre uzakta olduğumuzu söylesinler.
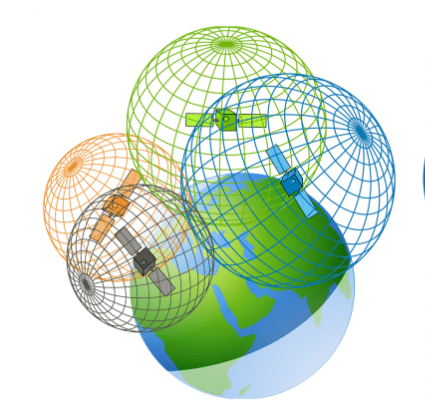
Sadece bu bilgiyle, bir harita üzerinde üç çember çizerek tam olarak nerede olduğumuzu anlayabiliriz. Bunun için, A kişisinin etrafında 3, B kişisinin etrafında 4 ve C kişisinin etrafında 3,5 metre yarıçaplı birer çember çizersek, bu üç çemberin kesiştiği nokta tam olarak bizim konumumuzdur. İşte bu aslında GPS’ in çalışma şeklidir. Tek bir farkla; 3 boyutlu uzayda insanlar yerine uydular kullanılır.
Her bir uydu sürekli olarak iki temel bilgi gönderir: Kendi konumu ve sinyalin gönderilme zamanı. Sizin GPS alıcınız ise bu sinyalleri alır, sinyali ne zaman aldığını not eder ve ne kadar sürede geldiğini hesaplar. Bu noktada basit ama önemli bir formül, yani yol=hız x zaman formülünü kullanarak aradaki mesafeyi bulabilir. Her GPS uydusu uzayda bir kürenin merkezi gibidir. Bu kürenin yarıçapı ise uydunun bizimle arasındaki mesafeye eşittir. Biraz önceki örnekte olduğu gibi, bu kürelerin kesişimi bize uzaydaki konumumuzu verecektir. Bu noktada şu bilgiyi eklemekte fayda var: GPS üzerine yapılan taptaze bir çalışmaya(5) göre uzaydaki konumumuzu kesin olarak belirleyebilmek için, 5 veya daha fazla uydudan gelen verinin hesaba katılması gerekir.
Şimdi bir örnek yardımıyla, işlerin nasıl yürüdüğünü anlamaya ve 4 uydu kullanarak konumumuzu bulmaya çalışalım. İlk olarak, deniz seviyesindeki her nokta için 
Şimdi uzaydaki konumumuzun 
Uydu 2 için elde edilen (E2) denklemi;
biçiminde olacaktır. Aynı işlemi diğer uydular için de yaparsak, yukarıdaki formatta yazılmış (E3) ve (E4) denklemlerini elde ederiz. İşlem sonunda tüm denklemlerin sağında ortak bir terim olduğu göreceğiz: 
(L1)=(E2)-(E1), (L2)=(E3)-(E2), (L3)=(E4)-(E3).
Örneğin (E1), 
Tabii ki gerçek hayattaki durum, burada verdiğimiz yaklaşımdan daha da karmaşıktır ve birçok hata kaynağı bulunur. Örneğin, sinyaller iyonosfer tabakasından geçerken yavaşlayabilir ve yön değiştirebilir. Hava durumu, nem oranı sinyal kalitesini etkileyebilir. Atomik saatler her ne kadar hassas olsalar da, küçük zaman hataları büyük konum hatalarına yol açabilir. GPS alıcısının kalitesi, elektronik gürültü ve işlem gücü gibi faktörler ölçüm hassasiyetini etkileyebilir. Hatta uyduların yörüngelerinde küçük sapmalar bile olabilir.
Tüm bu faktörler nedeniyle, günlük hayatta kullandığımız GPS cihazları genellikle birkaç metrelik hata payıyla çalışır ve daha hassas konum belirlemesi gereken durumlarda ek düzeltme sistemleri kullanılması gerekebilir. Örneğin, GPS’in konum doğruluğunu değerlendiren hata matrislerinde, özdeğerler (eigenvalues) yardımıyla konumlandırma hataları ve belirsizlikleri en aza indirgenmeye çalışılır.
Tüm zorluklara rağmen, GPS teknolojisi sürekli gelişmeye devam ediyor. Araştırmacılar daha hassas ölçümler için yeni matematiksel modeller geliştirirken, mühendisler daha güçlü sinyal işleme teknikleri üzerinde çalışıyor. Burada belki de en etkileyici olan, gündelik hayatımızda farkında bile olmadan kullandığımız bu sistemin, aslında yüzyıllar boyunca matematikçilerin soyut dünyalarında geliştirdikleri fikirlerin bir ürünü olması. Doğrusal cebir gibi teorik bir matematiğin, milyarlarca insanın hayatını kolaylaştıran somut bir teknolojiye dönüşmesi, bilimin evrensel dilinin gücünü gösteriyor.
KAYNAKLAR
1) https://tomrocksmaths.com/wp-content/uploads/2023/06/sunny-miao_-mathematical-approaches-to-global-positioning-systems.pdf
2) https://www.math.kent.edu/~reichel/courses/intr.num.comp.1/fall13/lecture4/project1.pdf
3) B. Kolman, D. A. Hill, Elementary Linear Algebra with Applications: Pearson New International Edition, 9th edition, 2013.
4) https://www.aeronomie.be/en/encyclopedia/ionosphere-influence-satellite-communication-gps
5) M. Boutin and G. Kemper. Global positioning: The uniqueness question and a new solution method. Advances in Applied Mathematics (2024).
6) https://gisgeography.com/trilateration-triangulation-gps/
Topolojik bir oluşum! 