Bir Fincan Kahveden Mutlak Gerçeklere : İspat Teknikleri Üzerine

Posted on 11 Eylül 2024 by esrakorkmaz

Matematiği diğer birçok bilimden farklı kılan şey nedir? Bu soruya yanıt vermek için önce, şimdiye kadar yazılmış en başarılı kitaplardan biri olan Öklid’in Elementlerinden ve onu zamandan bağımsız kılan özelliğinden bahsetmemiz gerekir.

Bildiğimiz gibi matematik ilk zamanlarda insanların ihtiyaçları doğrultusunda şekillenmiştir. Arazi ölçümleri, arenaların, su depolarının ve diğer pratik projelerin tasarımı için geometri ve trigonometri sorularının ele alınması gayet doğaldır. Kuşkusuz ki, üçgen, kare, dikdörtgen ve çember gibi kavramlar bu bağlamda doğal bir şekilde ortaya çıkmıştır.

Örneğin kareyi ele alalım: Ensiz ve herhangi bir kıvrılma/pürüz içermeyen 4 çizgiden oluşan bir şekil. Fakat burada, gerçeklikle örtüşmeyen bazı durumlar var. Yaşadığımız gezegenin geometrisi göz önüne alındığında, bu denli kusursuz bir şekli oluşturmak mümkün olabilir mi? Diğer taraftan, kağıt üzerine kalemle bir çizgi çizdiğimizde, genellikle çizginin genişliği olmadığını düşünürüz. Fakat aslında, kalemle yapılan herhangi bir fiziksel işaret, kalem ucunun boyutu veya mürekkebin kalınlığı nedeniyle bir miktar genişliğe sahip olacaktır.

Dolayısıyla, kare, çember, dikdörtgen vs. yalnızca idealize edilmiş birer kavram, yani birer tanımdan ibarettir. Matematik ise, tüm bu tanımlardan ve kabullerden yola çıkarak yeni doğrular elde etme sanatıdır. İşte bu doğrular silsilesinin temelini atan Öklid olmuştur. Bunun için işe nokta, doğru gibi bazı kavramların tanımıyla başlamıştır. “Doğru, ensiz bir uzunluktur” gibi. Sonra, adına postulat (belit) denilen su götürmez gerçeklerle yola devam eden Öklid, ortaya, bunları temel alan bazı iddialar atmıştır. (Bu tarz iddialara önerme de diyebiliriz.) İşte ortaya atılan bu iddiaların günümüzde hala geçerliliğini korumasını ve aslında, matematiğin eşsiz ve zamansız olmasını sağlayan şey ispatlardır.

İspat kavramının tarihi oldukça belirsizdir. Her ne kadar, modern standartlara uygun olmasa da, kayıtlara geçen ilk matematiksel ispat Babillilere aittir. Babilliler (Çinlilerle birlikte) Pisagor teoreminin Pisagor’dan çok daha önce farkına varmışlardı ve teoreminin neden doğru olduğunu gösteren bazı diyagramlara sahiptiler. Yine Öklid öncesi dönemde, Pisagor matematiksel, özellikle de geometrik ifadelerin, kesin ispat yoluyla doğrulanması gerektiğini vurgulamıştır. Tabii ki, kendi ismiyle anılan meşhur teoremi ispat etmiştir. 19. yüzyıldan başlayarak altın çağını yaşayan ispatlama yöntemi, biliyoruz ki halen matematiğin temelidir.

Peki ispat yapabilmek için ne gerekir? İlk olarak, matematiğin de tüm diğer diller gibi bir yapısı ve kuralları unutmamamız ve bu dili en azından bir öykü yazabilecek kadar öğrenmemiz gerekir. Sonrasında ise biraz ilham ve biraz da teknik yardımıyla sonuca ulaşmaya çalışırız. Şimdi, çok da kitabi bir anlatıma girmeden, daha çok örnekler üzerinden birkaç yöntem inceleyelim.

1) İspat yaparken, aslında bir kurgu oluşturduğumuzu ve bu kurgunun bir “giriş”, “gelişme” ve “sonuç” kısmı olması gerektiğini unutmayalım. Şimdi aşağıdaki örnek üzerinde bu kurguyu görmeye çalışalım:
Örnek: $f:A \rightarrow B$ ve $g: B \rightarrow C$ birer fonksiyon olmak üzere, $f$ ve $g$ bire-bir ise $g\circ f: A \rightarrow C$ de bire-birdir.
*Giriş: Bu kısmı, ‘elimizdeki veriler’ kısmı olarak düşünebiliriz. Sahip olduklarımız, bileşke tanımı, bire-birlik koşulu (yani, $h(a)=h(b) \Rightarrow a=b$ ) ve $f$ ile $g$ ‘nin bire-bir olması.
*Gelişme: Bu kısımda amacımıza yoğunlaşalım. Görmek istediğimiz şey, her $x,y \in A$ için $(g\circ f)(x) =(g\circ f)(y)$ ise $x=y$ olduğudur. O halde $(g\circ f)(x) =(g\circ f)(y)$ olduğunu kabul ederek ilk adımı atabiliriz. Amaca ulaşmak için, başlangıçta verilen malzemelere ihtiyaç duyarız. İlk olarak bileşke tanımından, $g(f(x))=g(f(y))$ olacaktır. O halde, $g$ bire-bir olduğundan $f(x)=f(y)$ elde edilir. Madem, $f$ de bire-bir, dolayısıyla buradan $x=y$ sonucuna ulaşılabilir.
*Sonuç: $(g\circ f)(x) =(g\circ f)(y)$ olması $x=y$ sonucunu doğurduğundan, $g\circ f$ bire-birdir.
Buradaki en önemli kısım varış noktasını önceden belirlemektir. Gelişme kısmının başında, neyi görürsek ispatın tamamlanacağını belirtip, sonra yola koyuluyoruz. Hani sonundan başlayan bazı filmler vardır. Sonrasında sizi flashback’lerle yeniden aynı sona götürmeye çalışırlar. Burada yaptığımız şey tam olarak bu aslında.

2) Bir ispatta önemli olan sadece doğru adımlar atmak değil, tüm bu adımları doğru sırayla atmaktır.
Örnek: Reel sayılar için cisim aksiyomlarını ve her $x\in \mathbb{R}$ için $x.0=0$ eşitliğini kullanarak $a(b-c)=ab-ac$ eşitliğinin sağlandığını ispatlayalım.
Elimizdeki bilgiler: Cisim aksiyomları, $x-y=x+(-y)$ ve $x.0=0$ eşitlikleri.
Şimdi aşağıdaki iki farklı ispat girişimini inceleyelim. Her ikisi de hemen hemen benzer adımlara sahip olmasına rağmen, yalnızca İspat1 doğru olandır. Çünkü eşitliğin sol tarafı ile başlar ve bizi elimizdeki malzemeler yardımıyla sonuca götürür. İspat2’de ise, gösterilmek istenen şey, daha ispatlanmadan doğru kabul edilmiştir.

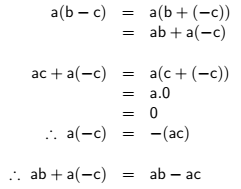
3) Bir iddiayı çürütmek (disprove) için ispata ihtiyaç duyulmaz. Örneğin, “mor fil yoktur” iddiasında bulunan birini yalanlamak için, ona bir adet mor fil göstermemiz yeterli olacaktır. Bu çoğu zaman ispat yapmaktan çok daha zor olabilir. Topolojiden basit bir örnek verelim:
Örnek: “Açık kümelerin keyfi arakesiti açıktır” iddiasını ters bir örnek (counterexample) yardımıyla çürütelim. Bunun için $\mathbb{R}$ ‘yi üzerindeki standart/doğal topolojiyle ele alalım. $\forall n\in \mathbb{N}$ için $(-\frac{1}{n}, \frac{1}{n})\subseteq \mathbb{R}$ açık aralıklarının keyfi/sonsuz arakesiti $\bigcap_{n\in \mathbb{N}} (-\frac{1}{n}, \frac{1}{n})=\{0\}$ olduğundan, keyfi kesişim kümesi kapalı bir kümedir.

4) Şimdi de kimi zaman ispata kimi zaman ise bir ters örneğe ihtiyaç duyulan durumlarla devam edelim. “Show/Prove that….” yani, “…. olduğunu gösteriniz” şeklinde bir soru ile karşılaştığımızda, en azından bir ispat tekniği belirleyip işe koyulabiliyoruz. Ama aşağıdaki örneklerde, aslında ilk olarak cevabın ne olduğunu sezgisel de olsa bulup, ona göre aksiyon almamız gerekiyor.
(a) Her sürekli fonksiyon türevlenebilir midir?
(b) $f: \mathbb{R}\mapsto \mathbb{R}$ sürekli, örten ve $K\subseteq \mathbb{R}$ bağlantılı olsun. Bu durumda $f(K)$ bağlantılı mıdır?
(c) $(0,1)$ aralığı $\mathbb{R}$ ‘ye homeomorfik, yani topolojik olarak eşyapılı mıdır?
(d) $[0,1]$ aralığı $\mathbb{R}$ ‘ye homeomorfik midir?

(a) ile başlayalım. Önce soruya sezgisel bir yaklaşım yapalım ve mesela zikzak şeklinde sürekli bir fonksiyon düşünelim.

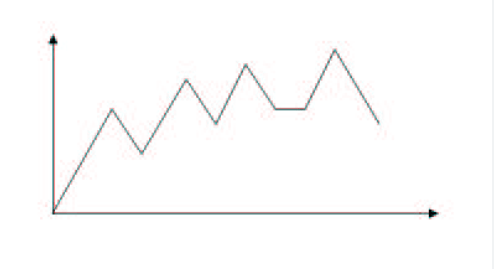
Sivri uçlar içeren böyle bir fonksiyonun, her noktada türevlenebilir olmasını bekleyemeyiz. Dolayısıyla bu iddianın doğru olmadığını keşfetmiş oluruz ve artık yapılması gereken şey, bir ters örnek bulmaya çalışmaktır.
(b)‘de iddia edilen gerçeği somut olarak görmek zor olabilir. Özellikle de $\mathbb{R}$ yerine $(X,\tau)$ gibi herhangi bir topolojik uzay üzerinde çalışıyorsak. Konu hakkında önceden bir bilgimiz olmadığında, ufak bir ispat denemesi yapıp, ispatta bir engelle karşılaşıyor muyuz diye bakmayı tercih edebiliriz. İddia yanlışsa, ispatın bir kısmında mutlaka sıkıntı yaşanacak, ek bir varsayıma ihtiyaç duyulacaktır. Bu soruda, verilen iddia doğru olduğu için işler tıkır tıkır ilerler. Fakat, örneğin $f$ ‘nin örten olduğu varsayımı verilmediğinde, ispatta bazı geçişleri yapmak mümkün olmayacaktır.
(c) ve (d) için de, önce tahminler üzerinden bir sonuca varmaya çalışıp sonra ispat/çürütme (prove/disprove) yapmamız gerekir. (İlgilenenler için: Burada $(0,1)$ ve $\mathbb{R}$ ‘nin bağlantılılık, kompaktlık, Hausdorff olma vs. gibi topolojik özelliklerinin farklı olup olmadığını kontrol edebiliriz. (c)’de herhangi bir fark olmaması bizi, bu iki uzay arasında bir homeomorfizma yazmaya itecektir. Fakat (d) ‘de işler pek de yolunda gitmiyor. [0,1]’den bir nokta çıkarmak, her zaman bağlantılılığı bozmazken (örneğin 0’ı ya da 1’i), $\mathbb{R}$ ‘den hangi noktayı çıkarırsak çıkaralım bağlantılılık bozuluyor. Dolayısıyla bu ikisi, topolojik olarak aynı şey değildir.)

5) Şimdi, $p\Rightarrow q$ ifadelerini nasıl ispatlayacağımızı inceleyelim. Bu formda verilen bir teoremi ispatlarken farklı teknikler kullanmak mümkündür. Şimdi aynı örneği 3 farklı ispat tekniği kullanarak kanıtlamaya çalışalım. Örneğe geçmeden önce birkaç bilgi/varsayım ile işe başlayalım.
İlk olarak $\mathbb{R}$ üzerinde limit/yığılma noktası tanımını hatırlayalım:
$A\subseteq \mathbb{R}$ ve $x \in A$ olmak üzere, eğer her $\epsilon>0$ için $B(x,\epsilon)\setminus \{x\} \cap A\neq \emptyset$ oluyorsa, yani $x$ noktasını içeren her açık aralık, $A$ ‘nın, $x$ dışında en az bir elemanını içeriyorsa, $x$ ‘e, $A$ ‘nın bir limit/yığılma noktası denir.
Tüm limit noktalarını içeren bir kümeye, kapalı küme denir.
Örnek: $A,B \subseteq \mathbb{R}$ kümeleri kapalı ise $A\cap B$ kümesi de kapalıdır.
Burada “ $p: A,B \subseteq \mathbb{R}$ kümeleri kapalıdır” ve “ $q: A\cap B$ kapalıdır” önermeleri veriliyor ve bizden $p\Rightarrow q$ ‘nun doğruluğunu göstermemiz isteniyor.

(a) İlk olarak doğrudan ispat yöntemi kullanalım. Bunun için yapmamız gereken, $p$ önermesinin doğru olduğunu kabul edip, $q$ önermesinin doğru olduğunu göstermektir. O halde $A$ ve $B$ ‘nin kapalı olduğunu varsayalım. $A\cap B$ ‘nin kapalı olduğunu göstermek için, bu kümenin keyfi bir $x$ limit noktasını alalım ve kümenin bu limit noktasını içerdiğini, yani $x\in A\cap B$ olduğunu gösterelim.
Öncelikle $x$ , $A\cap B$ ‘nin limit noktası olduğundan, tanım gereği, her $\epsilon>0$ için $B(x,\epsilon)\setminus \{x\} \cap (A\cap B) \neq \emptyset$ dir. Bu eşitsizliği $(B(x,\epsilon)\setminus \{x\} \cap A)) \cap (B(x,\epsilon)\setminus \{x\} \cap B) \neq \emptyset$ biçiminde de yazmak mümkündür. Buradan, $B(x,\epsilon)\setminus \{x\} \cap A \neq \emptyset$ ve $B(x,\epsilon)\setminus \{x\} \cap B \neq \emptyset$ olduğu görülebilir. Demek ki $x$ , hem $A$ hem de $B$ ‘nin limit noktasıdır. $A$ ve $B$ kümeleri kapalı olduğundan, her ikisi de bu limit noktasını içerir, yani $x\in A\cap B$ ‘dir.

(b) Şimdi de, dolaylı kanıt tekniklerinden biri olan kontrapozitif ispat kullanalım. $p\Rightarrow q$ ile $\sim q \Rightarrow \sim p$ (yani, $q^\prime \Rightarrow q^\prime)$ önermelerinin birbirlerine denk olduğunu biliyoruz. Bu nedenle, $p\Rightarrow q$ ‘yu ispatlamak yerine $\sim q \Rightarrow \sim p$ ‘yi ispatlamamız yeterli olacaktır. Bunun için $A\cap B$ ‘nin kapalı olmadığını varsayalım ve $A$ ‘nın ya da $B$ ‘nin kapalı olmadığını gösterelim.
Eğer $A\cap B$ kapalı değilse, $x\notin A\cap B$ olacak şekilde bir $x$ limit noktası vardır. $x\notin A\cap B$ ise $x\notin A$ ya da $x\notin B$ dir. Her iki durumu da inceleyelim: $x\notin A$ ise, $A$ kümesi tüm limit noktalarını içermiyor demektir. (Çünkü $x$ , $A\cap B$ ‘nin, dolayısıyla hem $A$ hem de $B$ ‘nin limit noktasıydı.) Bu nedenle $A$ kümesi kapalı değildir. Benzer şekilde, $x\notin B$ olduğunu varsayarak $B$ kümesinin kapalı olmadığı sonucuna ulaşabiliriz.

(c) Son yöntemimiz, yine dolaylı kanıt tekniklerinden biri olan olmayana ergi/çelişkiye varma (contradiction) yöntemi. Bu yöntemi kullanırken, önce $p$ önermesinin doğru olduğunu varsayıyoruz. Doğru olduğunu göstermek istediğimiz $q$ önermesinin ise yanlış olduğunu varsayıp çelişkiye varmaya çalışıyoruz. Yani aslında, $q$ ‘nun yanlış olduğu varsayımı, başımıza işler açıyor ve olmaması gereken sonuçlar doğuruyor. Bu nedenle biz de $q$ ‘nun doğru olması gerektiği sonucuna ulaşıyoruz.
O halde $A,B \subseteq \mathbb{R}$ ‘nin kapalı olduğunu, fakat tersine $A\cap B$ ‘nin kapalı olmadığını varsayalım. Eğer $A\cap B$ kapalı değilse, en az bir limit noktasını içermediğini, yani $x\notin A\cap B$ olacak şekilde bir $x$ limit noktasının olduğunu söyleyebiliriz. Bu noktadan sonra, (a) ile benzer gelişmeler yaşanacaktır. Yani, $x$ , “ $A\cap B$ ‘nin limit noktası olduğundan her $\epsilon>0$ için $B(x,\epsilon)\setminus \{x\} \cap (A\cap B) \neq \emptyset$ ” ile başlayan çıkarımlar dizinden, “ $x$ , hem $A$ hem de $B$ ‘nin limit noktasıdır” sonucuna ulaşırız. Bu noktada $A,B \subseteq \mathbb{R}$ ‘nin kapalı olduğu varsayımı gereği $x\in A$ ve $x\in B$ elde ederiz. Fakat dikkat edersek $x\notin A\cap B$ olduğunu varsaymıştık. Son elde ettiğimiz durum, bu varsayım ile çelişir. Demek ki, $A\cap B$ ‘nin kapalı olması gerekmektedir ve böylece ispat sonlanır.

6) Son olarak “varlık ispatları” konusuna değinelim. Yani bize, $\exists x P(x)$ formunda bir önerme verildiğinde bunu nasıl ispatlarız? Önce bu önermelere birkaç örnek verelim: “Pozitif tam sayıların küplerinin toplamı olarak, iki farklı şekilde yazılabilen bir pozitif tam sayı vardır“, “ $f, [a, b]\subseteq \mathbb{R}$ aralığı üzerinde sürekli bir fonksiyon olmak üzere, $f(a)< c < f(b)$ ise, $f(x) = c$ olacak şekilde bir $a<x<b$ vardır“.
Bu tarz ifadeleri ispatlamak için, yapısal (constructive) ve yapısal olmayan (non-constructive) olmak üzere iki farklı ispat çeşidi vardır. Yapısal ispatlar, önermeyi sağlayan nesnenin ne olduğununun ya da onun nasıl inşa edileceğinin veya bulunacağının açıkça ortaya koyulduğu bir yöntemdir. Örneğin, yazdığımız ilk örnek için, “1729 sayısı pozitif tam sayıların küplerinin toplamı olarak iki farklı şekilde yazılabilen pozitif bir tam sayıdır ( $1729=1^3+{12}^3=9^3+{10}^3$ )” dediğimizde, aslında yapısal bir ispat ortaya koymuş oluruz.
Bazı durumlarda ise, çözümü açıkça söylemesek bile, burada olduğu gibi nasıl inşa edileceği tarif ederiz. İşte constructive kelimesi de tam olarak buradan gelir.
Yapısal ispatların aksine, yapısal olmayan ispatlar bize çözümün ne olduğu ya da neye benzediği hakkında bir fikir vermez. Yani hiçbir inşa işine girmeden, “evet, bazı teoremler/önermeler gereği böyle bir nesne vardır” der ve ispatı tamamlarız.
Örnek: Her $x$ rasyonel sayısı için, $x\leq n$ olacak şekilde bir $n\in \mathbb{N}$ vardır.
Bunu ispatlamak için, bir $x$ rasyonel sayısı alalım ve tersine, istenilen koşulu sağlayan bir $n\in \mathbb{N}$ olmadığını kabul edelim. Bu durum aslında, bu $x$ sayısının, her $n\in \mathbb{N}$ için $x>n$ özelliğini sağladığı anlamına gelir. O halde, $1\in \mathbb{N}$ olduğundan $x>1$ ‘dir ve böylece $x=a/b$ ( $a,b \in \mathbb{N}, a>b$ ) biçiminde yazılabilir. Ayrıca, $a\in \mathbb{N}$ olduğundan $a> a/b$ dir ve buradan $1> 1/b$ ve böylece $1>b$ elde edilir. Fakat bu durum, $b\in \mathbb{N}$ olması ile çelişir. Bu hallere düşmemizin sebebinin, ispatın başında yaptığımız kabul olduğuna dikkat edelim. Demek ki, istenilen koşulu sağlayan bir $n\in \mathbb{N}$ olmalıdır. Ama nedir, neye benzer bilmiyoruz tabii.
(Bunu yapısal bir ispat kullanarak da göstermek mümkündür. Kabaca, $x=p/q, q\neq 0$ biçiminde yazıp $n=|p|+1$ olarak seçebiliriz.)

Tüm bu teknikleri bilmenin ve uygulamanın yanı sıra, nasıl bir yazım tekniği kullandığımız da oldukça önemlidir. Cümlelere matematiksel sembollerle başlamamak, cümleleri birbirlerine uygun bağlaçlar kullanarak, akıcılığı bozmayacak şekilde bağlamak, kullandığımız her kavramı açıklamak bunlardan sadece bazıları.

İspatlar hakkında söylenecek çok daha fazla şey, incelenmesi gereken çok daha fazla özel durum vardır. Yüzyıllarca ispatlamanın mümkün olmadığı, başına ödüller koyulan çetin cevizler, binlerce sayfalık kanıtlar, ilk olarak meşhur dört renk probleminin ispatlanmasıyla hayatımıza giren bilgisayar-destekli ispatlar…Matematiğin bu zengin ve karmaşık alanında derinliklerine indikçe, ispatların sonuçları doğrulamaktan çok daha fazlasını yaptıklarını fark edebiliriz. İspatlar yalnızca matematiğin değil, düşüncenin en güçlü araçlarından ve doğruya ulaşmanın, şüpheyi bilgeliğe dönüştürmenin en güzel yollarından biridir. Matematikçilerin üzerine düşen ise, Alfréd Rényi’nin de söylediği gibi, bir fincan kahveyi teoremlere, yani şık ispatlarla doğrulanmış mutlak gerçeklere dönüştürmektir.

KAYNAKLAR
1) https://livescience.com/earliest-form-of-pythagorean-triplet
2) https://ananddeopurkar.org/teaching/algebra1/cheng.pdf
3) https://www.math.wustl.edu/~sk/eolss.pdf
4) Richard H. Hammack,. Book of Proof, Open Textbook Library, 2013.
5) https://www.karlin.mff.cuni.cz/~krajicek/nature-scholze.pdf

Her şey birdenbire (mi) oldu II: Kapalı kümelerin ortaya çıkışı

Posted on 25 Mart 2021 by esrakorkmaz

Cevapla

Topoloji dersleri genelde, üç temel aksiyomla başlar. X bir küme ve $\tau$ , X’in kuvvet kümesinin bir alt ailesi olsun. Eğer,
(T1) $\emptyset \in \tau$ , $X \in \tau$
(T2) $G_1,G_2 \in \tau \Rightarrow G_1\cap G_2\in \tau$
(T3) $\forall \alpha, G_{\alpha} \in \tau \Rightarrow \bigcup G_ {\alpha} \in \tau$
özellikleri sağlanıyorsa $\tau$ ‘ya bir topoloji, $\tau$ ‘nun elemanlarına ise açık kümeler denir.
Sanki matematikçinin biri gelmiş ve demiş ki “Dostlar, yurttaşlar, dinleyin: Bundan sonra bu 3 aksiyomu sağlayan aile bir topolojik uzay olarak biline!” Tabii ki böyle olmamış ve bilimin her alanında olduğu gibi, bu tanım da zaman içinde evrilerek bu forma gelmiş. Hatta yapılan ilk tanımların “komşuluk” kavramını temel aldığını ve modern topolojinin bel kemiği olarak görülen açık kümelere uzun süreler ihtiyaç duyulmadığını bile söyleyebiliriz.

Bu yazıda, açık küme tanımına gelene kadar neler olup bittiğine, topolojinin hangi tanımlar çerçevesinde kimler tarafından inşa edildiğine bir bakacağız. (Tabii hikaye oldukça uzun olduğundan için bahsedemeyeceğimiz birçok kişi ve kavram da olacaktır.)

Topolojinin gelişimini üç ayrı koldan inceleyecek olsak, geometri, analiz ve fonksiyonel analizden yola çıkmamız doğru bir yaklaşım olurdu. Bir önceki yazımızda geometri ile ilişkisine kısaca değinmiştik. Burada yapacağımız şey ise analiz ile ilişkisini kurmak ve yakınsama kavramından yola çıkarak modern topolojiye doğru ilerlemek olacak.

Bir kümenin limit noktası (ya da orijinal ismiyle “Grenzpunkt”) kavramının isim babası ve bunun üzerine bir yayın yapan ilk kişi Cantor olmasına rağmen onu ilk bulan kişi Weierstrass’tır. 20 yılı aşkın süre boyunca devam eden derslerinde, Bolzano-Weierstrass teoreminin bir parçası olarak, bu kavramdan birçok kez bahsedilmiştir. Weierstrass bu teoremi topolojinin ya da orijinal ismiyle “analysis situs”un veya geometrinin değil, klasik analizin bir parçası olarak görmüştür. (Topoloji kelimesini kullanan ilk kişi Johann Benedict Listing’dir. “Vorstudien zur Topologie” adlı kitabının öncesinde yaptığı yazışmalarda da 10 yıl boyunca “Topologie” kelimesini kullanmıştır.) Teorem, n-boyutlu Öklid uzayında her sonsuz sınırlı kümenin bir limit noktası olduğunu ifade eder. Günümüzde Bolzano-Weierstrass teoremi olarak bilinmesine rağmen, Bolzano’nun çalışmalarında bu ifadeyi görmek imkansızdır çünkü daha ortada bir kümenin limit noktası kavramı yoktur. Bolzano’nun bulduğu şey Weierstrass’ın teoremi ispatlamakta kullandığı altaralıklara bölme yöntemine çok benzer bir metottur.
Weierstrass’ın derslerinde Bolzano-Weierstrass teoreminin birçok farklı ifadesi yer almıştır.
Teoremin bilinen ilk hali 1865 yılında, son hali ise 1886 yılında ifade edilmiştir.
(1865 yılında “Analitik fonksiyonlar teorisinin ilkeleri” isimli derste ifade edilen ve topolojide sıkça kullanılacak olan komşuluk tanımını içeren ifade şöyledir:
“Düzlemin sınırlı bir parçasında, verilen bir özelliğe sahip sonsuz sayıda nokta varsa, bu durumda (bu parçanın içinde ya da sınırında), her komşuluğunda bu özelliğe sahip sonsuz sayıda eleman bulunan en az bir nokta vardır.“)

İlginçtir ki, Weierstrass 20 yıl boyunca teoremin ifadesinde kullandığı bu noktaya herhangi bir isim vermemiştir. Onun yerine kariyerinin sonlarına doğru “Grenzstelle” terimini ortaya koymuştur. Burada şunu eklemek gerekir ki, “Grenzstelle” kümeye ait olamaz fakat Cantor’un “Grenzpunkt”u için böyle bir kısıtlama yoktur.

Cantor, 1872 yılında trigonometrik seriler üzerine yazdığı makalede, bir kümenin türev kümesini (yani, tüm limit noktalarının kümesini) tanımlamak için limit noktası terimini kullanmıştır. Şimdi Cantor’un tanımına bir bakalım:

“Bir P kümesinin limit noktasından anladığım şey, bir doğru üzerinde bulunan ve her komşuluğu P kümesinin sonsuz sayıda elemanını içeren bir noktadır. Limit noktası P kümesine de ait olabilir. Bir noktanın komşuluğundan kastedilen şey, noktayı içinde bulunduran bir aralıktır. Bu tanımlara dayanarak sonsuz sayıda nokta içeren her kümenin en az bir limit noktası olması gerektiğini kolayca gösterebiliriz.“

Yukarıdaki son cümle aslında Bolzano-Weierstrass teoreminin yayınlanmış ilk ifadesidir. Cantor bu teoreme herhangi bir referans vermemiş, ayrıca teorem sadece sınırlı bir küme üzerinde doğru olmasına rağmen, teoremin ifadesine böyle bir koşul eklememiştir. Bunun sebebi sadece bir dikkatsizlik olabilir. Çünkü 1882 yılında, bu teoremi ifade eden, kanıtlayan ve uygulayan ilk kişinin Weierstrass olduğunu söylemiştir. Weierstrass gibi, Cantor da Bolzano-Weierstrass teoremini klasik analizin bir parçası olarak düşünmüştür.

Kısa bir süre sonra, limit noktası kavramı İtalya’ya da ulaşmıştır. Ulisse Dini, reel analizin temelleri hakkında yazdığı kitapta, Bolzano-Weierstrass teoremini Cantor’un versiyonuna daha yakın fakat daha açık bir şekilde ifade etmiştir:

“Bir (a,b) aralığının sonsuz bir G altkümesinin (kümede olması gerekmeyen) bir limit noktası vardır.”

Cantor 1884 yılında, tüm limit noktalarını içeren küme olarak “kapalı küme” kavramını tanımlamıştır. Her kapalı kümenin bir türev kümesi olduğunu ve ayrıca $A \cup B$ kümesinin türev kümesinin, A’nın ve B’nin türev kümelerinin birleşimine eşit olduğunu göstermiştir. (Cantor’un bu özellikleri $\mathbb R$ üzerinde elde ettiğini unutmayalım.)

Cantor, açık küme kavramından bahsetmemesine rağmen, 1872’de bir aralığın, 1879 ise bir kümenin iç noktaları tanımlarını vermiştir. Cantor’un tanımı Giuseppe Peano’nun Geometric Applications of the Infinitesimal Calculus kitabında yapmış olduğu iç nokta tanımına yakındır. Peano’nun tanımı ise şöyledir:

“A kümesi $\mathbb{R}^n (n=1,2,3)$ ‘in bir alt kümesi olsun. Eğer, p ile arasındaki uzaklık r’den küçük olan tüm noktalar A’ya ait olacak şekilde bir r>0 varsa, p, A’nın iç noktasıdır denir.“

Peano ayrıca dış nokta (bir kümenin tümleyeninin iç noktaları) ve sınır noktası (ne iç ne de dış nokta olan noktalar) kavramlarını da tanımlamıştır.

Limit noktası kavramının Fransa’ya gelişi ise iki yolla olmuştur. Bunlardan ilki, Henri Poincare’nin 1883 yılında Klein gruplardan bahsettiği makalesinde Cantor’un türev kümesi gibi bazı tanımlarını kullanmasıdır. Poincare bu kavramların sadece Almanca isimlerini yazmış, ne anlama geldiklerini açıklamamıştır. İkincisi ise, Cantor’un makalelerinin Fransızca çevirilerini inceleyen Jules Tannery yardımıyla olmuştur. Tannery aynı zamanda, Peano’nun iç, dış ve sınır noktalarını tanımladığı kitabını da incelemiştir.

Bunların yanı sıra, Camille Jordan 1892 yılında belirli integraller üzerine yazdığı bir makalede Cantor’un fikirlerini kullanmıştır. Jordan’ın limit noktası tanımı Cantor’un tanımından farklıydı fakat tanımlanmasından 20 yıl sonra standart tanım haline gelecekti.

“Eğer her $\epsilon> 0$ için p ile q arasındaki uzaklık $\epsilon$ ‘dan küçük olacak şekilde bir $q\neq p, q\in E$ noktası varsa, p’ye E’nin limit noktası denir.“

Jordan da kapalı kümeleri tanımlamış fakat bu kümeleri kapalı küme değil mükemmel küme olarak adlandırmıştır. (Öte yandan Cantor mükemmel küme terimini, türev kümesine eşit olan kümeler için kullanmıştır.) Ayrıca, bir kümenin tümleyeninin türev kümesine ait olmayan noktaları iç nokta olarak adlandırmıştır. Jordan’ın da Cantor gibi, açık küme tanımını yapmaya çok yaklaştığını görüyoruz. Aslında tek yapması gereken, “iç noktaları kümesi kendisine eşit olan kümeye açık küme denir” tanımını yapmaktı fakat muhtemelen böyle bir kavrama ihtiyaç duymamıştı. Bunun yerine sınır noktalarını (ne kümenin ne de kümenin tümleyeninin iç noktası olan noktaları) tanımlamış ve sınır noktaları kümesinin boştan farklı ve kapalı bir küme olduğunu göstermiştir. 1983 yılında, limit tanımını biraz değiştirerek

“Eğer p noktası, E kümesinde bir dizinin limiti ise p’ye E’nin limit noktası denir”

tanımını vermiştir. (Bu tanımın ilk limit tanıma denk olduğunu göstermek için, o zamanlar daha ifade edilmemiş olan Seçme Aksiyomuna ihtiyaç vardır.)
(Bonus: Jordan ayrıca, n-boyutlu uzaylar üzerinde çalışırken günümüzde taksi-kap (taxi-cab) metriği olarak bilinen metriği tanımlamıştır.)

Görüyoruz ki derslerde kolayca tanımlayıp geçtiğimiz kavramlara ve ufak alıştırmalar şeklinde ispatladığımız ifadelere ulaşmak öyle kolay olmamış. Birçok matematikçinin katkısı ve tabii bir de uzunca bir zaman gerekmiş. Şuana kadar sadece kapalı kümeler, limit ve sınır noktaları, dış ve iç noktalardan bahsedip, açık küme kavramının etrafında dolanıp durduk. Açık kümeler nasıl tanımlanmış, topolojik uzay tanımı hep günümüzdeki gibi miymiş, yoksa o da zaman içinde sürekli değişerek ve en sonunda en iyinin hayatta kalması prensibine dayanarak mı bugünkü haline gelmiş? Yeni başlayanlar ve merak edenler için, bu soluk kesici (!) serüvene devam edeceğiz. “Her şey birdenbire (mi) oldu III” başlıklı yazımızda görüşmek üzere.

Kaynaklar
1) G.H. Moore, The emergence of open sets, closed sets, and limit points in analysis and topology, Historia Mathematica 35(3), 220-241 (2008)

Topolojik bir oluşum!

Tag Archives: limit noktası

Bir Fincan Kahveden Mutlak Gerçeklere : İspat Teknikleri Üzerine

Her şey birdenbire (mi) oldu II: Kapalı kümelerin ortaya çıkışı