Tag Archives: Komşuluk Sistemi

Anlamsız Gerçekler: Topolojide Boş Küme Meselesi

Posted on by
Cevapla

Önermeler liseden itibaren öğrenmeye başladığımız en temel konulardan biri. Mevcut lise eğitimi hakkında yorum yapacak kadar bilgi sahibi olmadığımdan, ispat yapmaya ve olan bitenin mantığını anlamaya yardımcı olacak bu konunun, lise aşamasında ne işe yaradığının gösterilip gösterilmediğini açıkçası bilmiyorum. Fakat 1. sınıflara bu konuyu anlatırken, ise (\Rightarrow) bağlacının doğruluk tablosu için şuan hatırlamadığım tuhaf bir ezber yöntemiyle karşılaşmış olmam sebebiyle, çoğu öğrenci tarafından yalnızca ekstra konu yükü olarak görüldüğünü düşünüyorum.

O zaman biz şimdi söz konusu ise (\Rightarrow) bağlacının doğruluk tablosu ile işe başlayalım ve aşağıdaki meşhur tabloya biraz yakından bakalım.

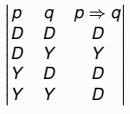
İlk olarak “yanlış bir önermeden yine yanlış bir önerme çıkması mümkün müdür?” sorusuna yanıt arayalım. “p: 0=1” önermesi olsun. p’nin yanlış bir önerme olduğu gayet açıktır. Bu önermede, eşitliğin her iki yanına 1 eklersek, “q: 1=2” yanlış önermesini elde ederiz. Yani “0=1 ise 1=2” olur. Bu ise “Y \Rightarrow Y \equiv D” olduğuna dair gayet güzel bir örnektir.

Yine “p: 0=1” önermesini ele alalım. 0=1 ise 1=0 olduğu açıktır. Şimdi bu iki eşitliği alt alta yazıp, taraf tarafa toplayalım ve “q: 1=1” doğru önermesini elde edelim. Bakın burada yanlış bir önerme ile yola çıkıp, doğru bir önerme elde ettik ve böylece “Y \Rightarrow D \equiv D” olacak şekilde bir örnek bulmuş olduk.

Bu konuda filozof matematikçi Bertrand Russell’ın şöyle bir anekdotu vardır. Russell bir gün sınıfında, yanlış varsayımlarla istenilen her şeyin doğruluğunun gösterilebileceğinden bahsetmiştir. Bunun üzerine bir öğrencisi ondan 1=0 olduğunu kabul ederek, kendinin Papa olduğunu ispatlamasını istemiştir. Russell’ın bu soruya cevabı ise şöyledir:

0 = 1 olduğunu varsayalım. Eşitliğin her iki tarafına 1 eklersek 1=2 olur. Papa ile beni bir odaya koyarsanız odada 2 kişi olacaktır. Fakat 2 = 1 olduğundan odada aslında 1 kişi olduğunu söyleyebiliriz. Yani, ben Papa’yım.

Şimdi de \Rightarrow bağlacının doğruluk tablosunu bir örnekle anlamaya çalışalım. Bir arkadaşınız size, “Derslere katılmazsan, matematik bölümünden mezun olamazsın” diyor. Burada “p: Derslere katılmıyorsun” ve “q: Matematik bölümünden mezun olamadın” önermeleri olsun ve biz arkadaşımızın söylediği p\Rightarrow q önermesinin doğruluk değerini inceleyelim. Bunun için tüm ihtimalleri gözden geçirelim:

  1. Derslere katılmazsınız ve mezun olamazsınız. (p\equiv D, q\equiv D)
  2. Derslere katılmazsınız ve mezun olursunuz. (p\equiv D, q\equiv Y)
  3. Derslere katılırsınız ve mezun olamazsınız. (p\equiv Y, q\equiv D)
  4. Derslere katılırsınız ve mezun olursunuz. (p\equiv Y, q\equiv Y)

Burada arkadaşınızın doğruyu söylemediği tek durum 2. durumdur. Çünkü derslere katılmadınız fakat mezun oldunuz. Yani D\Rightarrow Y\equiv Y oldu. 1. durumun doğruluğu ise (D\Rightarrow D\equiv D) gayet açıktır. 3. ve 4. durumda da arkadaşınızın doğruyu söylemediğini iddia edemezsiniz çünkü derse katılırsanız ne olacağı konusunda bir fikir beyan etmemişti. Demek ki Y\Rightarrow D\equiv D ve Y\Rightarrow Y\equiv D‘dir.

İşte yukarıda anlattığımız ufacık \Rightarrow bağlacının, olmaz gibi görünen bazı şeyleri oldurmaya gücü yetiyor. Nasıl mı? Bunun için artık asıl konumuza giriş yapalım ve boş kümenin topoloji tanımında ne işi var, olmasaydı başımıza ne işler açardı, ona bir bakalım.

Bunun için önce açık kümelerin komşuluklar yardımıyla tanımını hatırlayalım. X bir küme ve \mathcal{U}_x bir komşuluk sistemi olsun. Burumda G\subseteq X kümesinin açık olması için gerek ve yeter koşul her x\in G için U\subseteq G olacak şekilde bir U\in \mathcal{U}_x olmasıdır. Diğer bir deyişle, her x için, “x\in G \Rightarrow \exists U\in \mathcal{U}_x ; U\subseteq G” koşulu sağlanmalıdır. Dikkat edersek \emptyset bu koşulu sağlıyor çünkü önermenin x\in \emptyset kısmı her zaman yanlış oluyor. Bu nedenle, \Rightarrow önermesinin özelliği gereği, diğer kısmının doğruluğu ya da yanlışlığı bizi pek de ilgilendirmiyor. (Y\Rightarrow D\equiv D ve Y\Rightarrow Y\equiv D olduğunu hatırlayalım.)

Burada olduğu gibi, sadece öncülü (yani ise önermesinin sol kısmı) yanlış olduğu için doğru olan durumlar, mantıkta anlamsız gerçek (vacuous truth) olarak adlandırılıyor. Örneğin bulunduğunuz odada hiç cep telefonu yoksa “Odadaki tüm cep telefonları açıktır” ifadesi bir anlamsız gerçektir. (“p: Cep telefonu odadadır. q: Cep telefonu çalıyor” gibi düşünebilirsiniz. ) Anneler babalar dikkat: Mantık diyor ki, eğer çocuğunuz tabağına hiç yemek koymamışsa ve “tabağımdaki tüm yemekleri yedim” diyorsa, teknik olarak size doğruyu söylemiş oluyor.

Boş kümenin topolojide olması da anlamsız bir gerçek olabilir fakat bizi bir çok yükten kurtarıyor. Örneğin topoloji tanımındaki “iki açık kümenin kesişimi de açıktır” koşulunu ele alalım. Eğer boş küme açık olmasaydı, ayrık (yani kesişimleri boş küme olan) iki açık küme aldığınızda kesişimleri açık olmayacaktı. Dolayısıyla tanımı “ayrık olmayan iki açık kümenin kesişimi” olarak güncellemeniz gerekecekti. Ayrıca birçok ispatta elinizdeki kümelerin ayrık olması ihtimalini ayrıca incelemeniz gerekecek, ayrık olmaları hiç işinize gelmeyecek ve bunun olması ihtimali bile sizi ürkütmeye yetecekti.

Diğer taraftan, kapalı kümeler açık kümelerin tümleyenleri olduğundan, X kapalı bir küme olmayacak, bu nedenle X‘in kapanışı nedir sorusu cevapsız kalacaktı. Ayrıca, en basitinden f: (X,\tau_1)\rightarrow (Y,\tau_2), f(x)=c sabit fonksiyonu bile sürekli olmayacaktı. Çünkü c\notin G olacak şekildeki G\in \tau_2 için, f^{-1}(G)=\emptyset \notin \tau_1 olacaktı.

Son bir gözlem: Burada bahsetmiş olduğum “boş ailenin birleşiminin boş olması” gerçeğini ve açık küme aksiyomlarından biri olan “açık kümelerin keyfi birleşimi açıktır” koşulunu kullanarak da boş kümenin topolojide olacağı gerçeğine ulaşabilmek mümkündür.

KAYNAKLAR
1) Ali Nesin, Önermeler Mantığı, Bilgi Üniversitesi Yayınları, 2001.
2) https://en.wikipedia.org/wiki/Vacuous_truth
3) https://nesinkoyleri.org/wp-content/uploads/2019/05/zafer_ercan-topoloji.pdf