Jordan eğri teoremi | Topolojik bir oluşum!

Matematikte bazı gerçekler öylesine bariz ve kolay anlaşılır gibi görünür ki, onları sorgulamak aklımızın ucundan bile geçmez. Ancak konu matematiksel ispata geldiğinde, bu apaçık gerçeklerin ardında, uzun süren mücadeleler, zekice kurgulanmış ispatlar ve bazen de çözülemeyen gizemlerin yattığını fark ederiz. Bunun en bilinen örneklerinden biri “Eğer $n>2$ bir tam sayı ise $x^n + y^n = z^n$ denklemi sağlayan pozitif $x, y, z$ üçlüleri bulunamaz” ifadesiyle bilinen Fermat’nın son teoremidir. Fermat’nın 1640 yılında, yanına iliştirdiği “Bunun gerçekten harika bir ispatını buldum, fakat bu sayfanın kenarı onu yazmak için çok dar!” minvalinde bir not ile matematik dünyasına miras bıraktığı bu muamma, matematikçileri 358 yıl boyunca uğraştırmıştır. Teorem popüler kültürde de oldukça ilgi çekmiş, kitaplarda (Fermat’s Enigma, Fermat’s Last Theorem, Papağan Teoremi), dizi ve filmlerde (Oxford Cinayetleri, La habitacion de Fermat, Fermat’s Last Tango, Simpsons) kendisinden söz ettirmiştir. Diğer bir örnek, herhangi bir haritayı, komşu ülkelerin aynı renkte olmaması koşuluyla, en fazla dört renk kullanarak renklendirebileceğimizi ifade eden dört renk teoremidir. 1852 yılında ortaya atılan bu teorem, ancak 1976’da, 1200 saatlik bilgisayar hesabı yardımıyla kanıtlanana dek çözülememiş bir problem olarak kalmıştır.
Bu iki meşhur teorem aslında, matematiğin aşikâr sandığımız gerçekleri bile ne denli derinlemesine inceleyip kanıtlamaya çalıştığını gösterir. Bu yazımızda, bu durumun bir diğer çarpıcı örneği olan Jordan Eğri Teoremi’nden bahsedeceğiz.

Jordan Eğri Teoremi, Fransız matematikçi Camille Jordan tarafından 1887 yılında ortaya atılmıştır. Teorem, sürekli (herhangi bir boşluk ya da delik içermeyen), kendini kesmeyen ve kapalı, (yani kısaca basit kapalı) bir eğrinin düzlemi iç ve dış olarak adlandırılan iki ayrı parçaya böldüğünü söyler. Burada, “basit kapalı eğri” yerine “Jordan eğri” ifadesini de kullanabiliriz. Bir Jordan eğri, topolojik olarak bir çembere denktir, yani çemberle aralarında bir homeomorfizma tanımlanabilir.

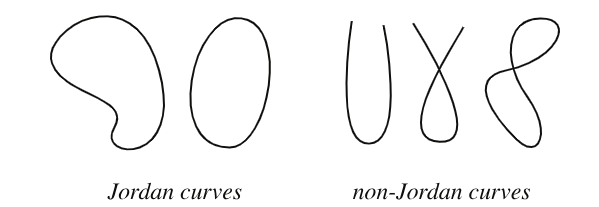
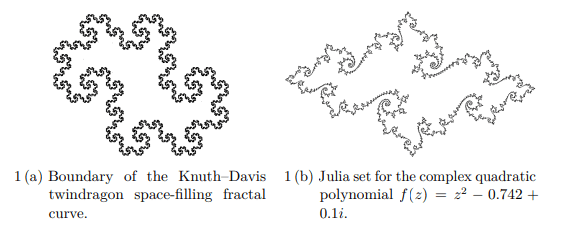
https://mathworld.wolfram.com/JordanCurve.html

Kulağa çok açık ve net geliyor değil mi? Sonuçta bir çember çizdiğimizde, çemberin içi ve dışı olmak üzere iki bölge oluşur ve bu bölgeleri tespit etmek gayet kolaydır. Peki ya eğrimiz çember gibi ideal bir eğri değilse? Sonuçta Felix Klein’in de söylediği gibi “Herkes bir eğrinin ne demek olduğunu bilir, ta ki yeterince matematik öğrenip sayısız istisnayı görene kadar.” Klein’i doğrular şekilde, bir Jordan eğrisi çok karmaşık ve hatta hiçbir noktada türevlenemeyen bir eğri dahi olabilir. Örneğin; Şekil 1(a)’daki Knuth-Davis twindragon space-filling fraktal eğrisinin sınırı veya 1(b)’deki $f(z)=z^2-0.742+0.1i$ kompleks kuadratik polinomunun Julia kümesi gibi.

Ya da, içerisini ve dışarısını ayırt etmek oldukça zor olabilir. Örneğin, Fiona Ross’un tek bir çizgiyle oluşturduğu ve bize içeri-dışarı kavramlarını sorgulattığı labirent benzeri çizimlerinde olduğu gibi.

*When we could be diving for pearls*, Fiona Ross, 2011

Hatta her ne kadar günlük hayatta karşılaşmasak da, matematiksel olarak, uzunluğu sonsuz olmasına rağmen pozitif alan kaplayan Jordan eğrileri de tanımlanabilir. Bu eğrilerin en güzel örneği, 1903 yılında William Fogg Osgood tarafından tanımlanan Osgood eğrisidir. Aşağıdaki şekilde bu eğrinin, bir eşkenar üçgenden sonsuz sayıda üçgen dilimi çıkarılarak oluşturulan bir örneğini görebiliriz. (Sonsuz bir eğri olduğundan, çizimin, bu eğrinin kendisi değil, bir yaklaşımı olduğunu unutmayalım!)

Osgood eğrisi, https://en.wikipedia.org/wiki/Osgood_curve

Normalde bir çizgiyi/eğriyi düşündüğümüzde, onun genişliğini ihmal eder ve dolayısıyla alanını sıfır olarak kabul ederiz. Osgood eğrisini ilginç kılan, eğrinin çevrelediği alanın değil, eğrinin kendisinin kapladığı alanın pozitif olmasıdır. Fakat burada her ne kadar ‘alan’ kelimesi kullanılmış olsa da, pozitif alan kaplamak ile kast edilen, eğrinin pozitif bir Lebesque ölçüsüne sahip olmasıdır.

Tam bu noktada, konudan biraz sapmayı göze alıp, bu Lebesque ölçüsü meselesine ufak bir açıklık getirelim. Biliyoruz ki, bir çubuğun uzunluğunu ölçerken başlangıç ve bitiş noktalarını belirleriz ve aradaki mesafeyi hesaplarız. Örneğin, [0,1] aralığının uzunluğu 1 birimdir. Fakat bu yöntem bazı durumlarda işe yaramaz. Örneğin, bir noktanın uzunluğu sıfırdır. Bu durumda sayılabilir ya da sayılamaz sonsuzlukta noktadan oluşan bir küme nasıl ölçülür? İşte burada Lebesgue ölçüsü devreye girer. Lebesgue ölçüsü, büyüklük veya uzunluk kavramını genelleştirerek, klasik ölçünün yeterli olmadığı, karmaşık ve hatta bazen patolojik kümelerin ölçümünü daha tutarlı ve kullanışlı bir şekilde ele almanın bir yolunu sunar. Tabii bu genelleştirme yapılırken, herhangi bir kümenin ölçüsünün negatif olmaması, kümeyi belirli bir miktar kaydırdığımızda ölçüsünün değişmemesi gibi, bir ölçümden beklediğimiz bazı sezgisel özelliklerin korunmasına da dikkat edilmiştir.

Lebesgue ölçüsünü, kümeyi aynı özelliğe sahip noktaların oluşturduğu alt kümelere ayırıp, ardından bu alt kümelerin uzunluklarını (veya genel olarak ölçülerini) toplayan bir sistem olarak düşünebiliriz. Örneğin, [0,1] aralığından başlayarak, her aralığın orta üçte birinin yinelemeli olarak çıkarılmasıyla oluşturulan Cantor kümesini ele alalım.

Kaynak:https://brilliant.org/wiki/cantor-set/

Çıkarılan her bir parçanın uzunluğunu toplayarak oluşturulan sonsuz seriden yararlanarak, Cantor kümesinin Lebesque ölçüsünü bulmak mümkündür.
Ya da, sayılabilir bir küme olan $[0,1]\cap \mathbb{Q}$ kümesinin ölçümünün sıfır olması ve bu nedenle [0,1] aralığındaki irrasyonel sayılar kümesinin ölçümünün 1 olması gibi sonuçlara ulaşmak da mümkündür.

Yeniden Osgood eğrisine dönecek olursak, pozitif alan meselesini, sonsuz uzunlukta bir ipi sürekli zikzaklar çizerek yerleştirdiğimizde, küçük de olsa bir alan yaratmasını sağlayabilecekmişiz gibi hissetmemize benzetebiliriz. Osgood eğrisini elde ederken tekrarlanan üçgen çıkarma işlemi sonsuza kadar sürdüğünden, eğrinin sınırları giderek daha fazla alanı kaplayacak ve aradaki boşluklar azalacakmış gibi düşünebiliriz.

Gördüğümüz gibi Jordan’ın teoreminin kapsamına giren böyle ilginç eğrilerin olması, işleri oldukça karışık bir hale getirebiliyor. Dolayısıyla, teoremin tamamlanmış ispatlarında kullanılan homoloji veya cebirsel topolojik kavramlar bir yana, modern topolojinin bile tam anlamıyla isminin koyulmadığı yıllarda bunlarla uğraşan Jordan’ın işi aslında bir hayli zor görünüyor. Zaten yapmış olduğu ispatın, her ne kadar sezgisel olarak doğru görünse de, modern anlamda tüm olası Jordan eğrilerini kapsayan eksiksiz bir ispat olmadığı düşünülüyor. (İspat hakkındaki iddiaları merak edenler buradan devam edebilirler.) Çünkü Jordan, her noktasında türevlenebilir olan (düzgün/smooth), fraktal benzeri yapılar oluşturmayan sorunsuz eğrilerle çalışmıştır.
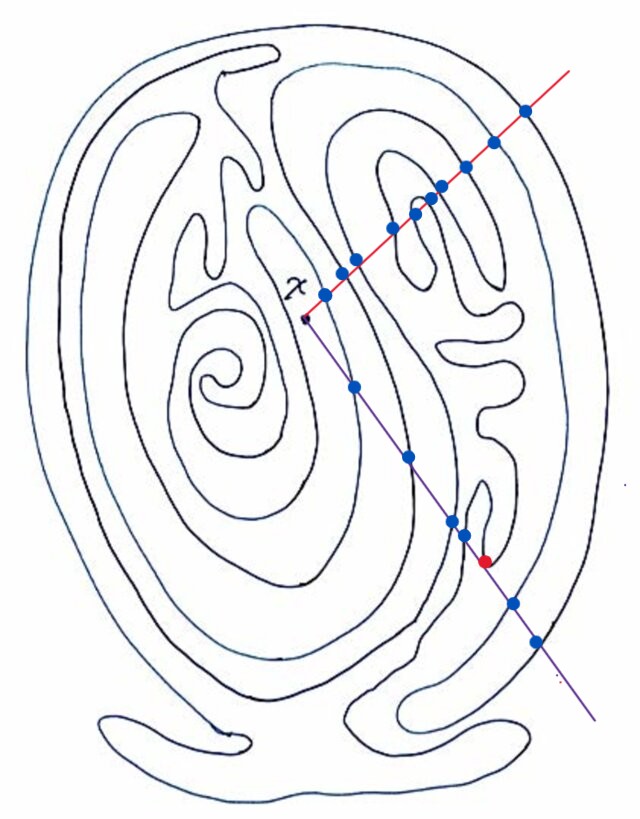
İspatında ise iç-dış ayrımı yapmak için şu yöntemi kullanmıştır: Eğrinin üzerinde olmayan bir nokta aldığımızı düşünelim. Noktamızdan sonsuza doğru bir ışın gönderelim. (Tutarsızlığı önlemek için, ışınları çizerken sabit bir yön belirleyip tüm noktalar için o yönü kullanmayı tercih edebiliriz.) Şimdi, bu ışınımızın, eğriyle kaç kez kesiştiğini sayalım. Işının eğriyi tek sayıda kesmesi noktanın içeride, çift sayıda kesmesi dışarıda olduğunu gösterir. (Çember üzerinde yapacağımız basit bir testle bunu kolayca görebiliriz.) Eğer çizgimiz bir tepe noktasına dokunuyorsa, işler biraz karışır. Eğrinin o tepe noktasına giren iki kenarı da ışınımızın aynı tarafında kalıyorsa, bunu bir kesişme olarak saymayız. Kenarlar farklı tarafta kalıyorsa sayabiliriz. Örneğin aşağıdaki şekilde seçilmiş olan $x$ noktasından çizilen ışınlar Jordan eğrisini çift sayıda keser. Altta çizdiğimiz (mor ışın) 7 noktada kesiyor gibi görünse de, kırmızı kesişme noktasında, eğrimizin iki kolu da ışının aynı tarafında (sağında) kaldığı için bunu bir kesişme olarak sayamayız. Dolasıyla $x$ noktası eğrinin dışında bir noktadır.

Jordan’dan yıllar sonra 1905’te Oswald Veblen, Jordan Eğri Teoremi için daha sağlam bir ispat sunmuştur. Jordan’ın ispatındaki boşlukları fark eden Veblen, eğrinin düzlemi iki ayrı bölgeye ayırdığını göstermek için topolojik yöntemler kullanmıştır. Veblen, düzlemi üçgenselleştirme gibi teknikler kullanarak, eğrinin iç ve dış bölgelerini daha detaylı bir şekilde analiz etmiş, bu bölgelerin bağlantılılık özelliklerini açığa çıkarmıştır. Çalışmasında, teoremin ispatını önce poligonlar üzerinde vermiştir. Sonra, genel Jordan eğrilerine poligonlarla istenildiği kadar iyi bir şekilde yaklaşılabileceğini ve süreklilik kavramı yardımıyla, poligonlarla yaklaşılan eğrilerin özelliklerinin, genel Jordan eğrisinin özelliklerine yakınsadığını göstermiştir. Böylece, poligonlar için ispatlanan teoremin, genel duruma genelleştirilebilmesi mümkün olmuştur. Tüm bu yaklaşımlarıyla Veblen, teoremin ilk kesin kanıtını veren kişi olmuştur fakat yine de ispat tüm Jordan eğrilerini kapsamaz.
Görüldüğü gibi teoremi tam olarak kanıtlamak için matematikçiler uzun bir süre ter dökmüştür. Jordan’ın ilk denemesiyle başlayan bu matematiksel macera, de la Vallée Poussin, Schoenflies, Brouwer, Alexander, Kerékjártó ve Denjoy gibi dönemin önde gelen matematikçilerinin kolları sıvayıp, topoloji, kompleks analiz ve geometri gibi farklı alanları harmanlayarak bu sezgisel ama bir o kadar da girift teoremi kanıtlamaları ile devam etmiştir. Ayrıca, Filippov‘dan Tverberg‘e, Narens‘ten Thomassen‘e kadar birçok matematikçi, standart olmayan analizden (nonstandard analysis) Brouwer sabit nokta teoremine, yapısal (constructive) matematikten çizge teorisine kadar farklı yaklaşımlarla yeni ve daha basit kanıtlar üretmeye devam etmişlerdir.

Jordan Eğri Teoremi, topolojinin temel taşlarından biri olmanın çok ötesinde, modern matematik ve mühendisliğin sayısız uygulamasında sessizce işleyen bir prensiptir. Günlük hayatta karşımıza çıkmasa da, teoremin sağladığı iç-dış ayrımı prensibi, bilgisayar grafikleri, robotik, coğrafi bilgi sistemleri gibi çeşitli alanlarda dolaylı olarak kullanılır. Ancak asıl büyüleyici olan, bu teoremin, matematiğin bizi bazen nasıl şaşırtabileceğine dair çarpıcı bir ayna tutmasıdır. Bizleri, sezgilerimizin bizi yanıltabileceği, en basit görünen soruların bile karmaşık cevaplar içerebileceği ve matematiksel ispatın, bizi kesinliğe ve derin anlayışa ulaştıran yegane araç olduğu gerçeğiyle yüzleştirir. Ve son olarak bize şunu hatırlatır: İnsanlığın, “apaçık” olanın ötesindeki sır perdesini aralama tutkusu, hiç kuşkusuz sonsuza dek devam edecektir.

KAYNAKLAR
1) https://www.maths.ed.ac.uk/~v1ranick/jordan/index.htm
2) https://www.maths.ed.ac.uk/~v1ranick/jordan/maehara.pdf
3) https://facultystaff.richmond.edu/~wross/pdf/Jordan.pdf
4) https://www.uni-ulm.de/fileadmin/website_uni_ulm/mawi.inst.020/sauter/files/Sauter-TwistedJordan.2017.usem20.pdf
5) https://brilliant.org/wiki/cantor-set/
6) https://www.math.unm.edu/~crisp/courses/math402/spring16/CantorSet.pdf
7) https://nebusresearch.wordpress.com/2016/07/07/theorem-thursday-the-jordan-curve-theorem/
8) P. Coggins, Active learning for development of a conceptual understanding of the jordan curve theorem for preservice elementary education majors and non-mathematics majors, 12th annual International Conference of Education, Research and Innovation, 2019.
9) O. Veblen, Theory on Plane Curves in Non-Metrical Analysis Situs. Transactions of the American Mathematical Society, 6(1), 83–98, 1905.

Bir önceki yazıda, matematikte sezgiye aykırı nesnelerden ve böyle nesnelerle oynamanın matematik severler için tam bir eğlence kaynağı olduğundan bahsetmiştik. Tabii bir de sırtımızı Asimov’a dayayarak bu konuda ne kadar haklı olduğumuz konusundaki fikrimizi pekiştirmiştik.

O zaman aklımızın sınırlarını zorlayan bu nesneleri anlatmaya devam edelim. Sıradaki örneğimiz topolojiden gelecek ama öncesinde hangi kanıyı çürütmek amacıyla tanımlandığından kısaca bahsetmek gerekiyor.

Düzlemde kendini kesmeyen kapalı bir eğriye basit kapalı eğri (simple closed curve) ya da bir Jordan eğrisi denir. Örneğin çember ve elips birer basit kapalı eğridir. 1887 yılında Fransız matematikçi Camille Jordan, bu eğriler üzerine, görünüşte “ee ne var bunda” denilebilecek fakat ispatlaması hiç de kolay olmayan bir teorem ortaya koymuştur. Jordan eğri teoremi olarak bilinen bu teoremin ifadesi şöyledir:

Düzlemde her basit kapalı eğri (“her Jordan eğrisi” diyecek hali yok tabii) düzlemi iç ve dış olmak üzere iki bölgeye ayırır. Yani tam olarak şöyle bir şey. Jordan, teoremi ispatlamış ispatlamasına ama maalesef kanıtı hatalıymış. Teoremin ilk doğru ispatı 1905’te Amerikalı matematikçi Oswald Veblen tarafından yapılmıştır. Daha sonra Arthur Schoenflies bunu görmüş ve arttırmış ve “Elde edilen bu iki bölge düzlemde bir çemberin içine ve dışına homeomorfiktir” demiştir.

Peki acaba Schoenflies’in iddiasının üç boyutta doğru olmadığına dair bir örnek verilebilir mi? Yani uzayı iki parçaya ayırsa da, içi ve dışı kürenin içine ve dışına homeomorfik olmayacak şekilde bir nesne bulmak mümkün olabilir mi? İşte bu soruya yanıt veren, 1924 yılında yayınladığı ve iki sayfa bile sürmeyen An Example of a Simply Connected Surface Bounding a Region which is not Simply Connected isimli çalışmasıyla James Waddell Alexander olmuştur. Basit bağlantılılığın bu işle ne ilgisi olduğunu biraz sonra anlayacağız ama biz önce Alexander’ın ortaya koyduğu örneğe bir bakalım. İşte karşınızda Alexander’ın Boynuzlu Küresi:

Oldukça karışık görünen bu nesnenin nasıl oluşturulduğuna birlikte bakalım.

Önce bir küre alalım ve üzerine iki disk çizip bunları yukarı doğru iki parmak ya da boynuz gibi çektiğimizi düşünelim. Burada boynuzların uçları karşılıklı birer disk şeklinde olacak ve birbirine asla değmeyecek. Daha sonra her bir diskten ikişer boynuz çıkarıp aşağıdaki gibi birbirine kenetleyelim.

Şuan elimizde bir öncekinden daha küçük dört adet disk var. Bunların her birinden yine ikişer boynuz çıkararak işleme devam ediyoruz ve bu işlemi sonsuza kadar sürdürüyoruz. İşte bu şekilde elde edilen nesne Alexander’ın boynuzlu küresi olarak adlandırılır ve bu gerçekten de bir küredir, yani en azından topolojik olarak. Bunun sebebi aslında elde ettiğimiz diskleri birbirine çok yaklaştırsak da asla birleştirmememiz. Örneğin yukarıdaki şeklin bir oyun hamurundan yapıldığını düşünürsek, hiçbir parçayı kırmaya ya da kesmeye gerek duymadan, boynuzları iterek şekli ilk haline döndürebiliriz.

Bu kürenin içinin açık (yani sınırı dahil olmayan) bir top olduğunu ve bu nedenle bir kürenin içine homeomorfik olduğunu söyleyebiliriz. Fakat dışı standart bir kürenin dışına homeomorfik olmaz. Bunun için, daha önce burada bahsetmiş olduğumuz basit bağlantılılık tanımını hatırlayalım. Kürenin dışında aldığımız her kapalı eğriyi, yine kürenin dışında kalacak bir noktaya büzebildiğimiz için, kürenin dışı basit bağlantılıdır. Diğer taraftan boynuzlu kürenin dışı basit bağlantılı değildir.

Bunu görmek için kürenin dışında yukarıdaki gibi kapalı bir eğri alalım. Bu eğriyi boynuzlu küreden dışarı çıkarmak için paralel disklerin arasına taşımamız gerekir. Hatırlarsak paralel diskleri elde etme sürecimiz sonsuz bir süreçti. Dolayısıyla eğriyi taşıdığımız diskler küçüldükçe eğri de küreye yaklaşacak, hatta bir yerden sonra değecektir. Bu nedenle eğriyi kürenin dışında bir noktaya büzme hayallerimiz de suya düşer.

Demek ki boynuzlu kürenin dışı, standart bir kürenin dışına homeomorfik değildir, yani Schoenflies’in teoremi üç boyutta geçerli olmaz. Bu örneğe rağmen matematikçiler bu teoremin hangi nesneler sınıfı üzerinde doğru olacağını araştırmaya devam etmişlerdir. Bu konuda (birbirlerinden bağımsız olarak) başarıya ulaşan Brown ve Mazur teoriye katkılarından ötürü Veblen ödülüne layık görülmüşlerdir. Hani Jordan’dan yıllar sonra, onun teoremine ilk doğru ispatı veren Oswald Veblen vardı ya, işte onun anısına verilen geometri/topoloji ödülüne.

Bir sonraki yazıda algı kapılarını en az boynuzlu küre kadar zorlayan bir başka örnekle devam edeceğiz ve aşağıdaki gibi, kafasında bir boynuzlu küre ile resmedilen adamın tanımlamış olduğu ilginç fonksiyonu inceleyeceğiz.

(Dipnot: Son olarak, adam deyip geçmeden, geçen sene COVID-19 sebebiyle kaybettiğimiz Conway‘in eşsiz bir zekaya sahip olduğunu hatırlatmak isterim.)

John Horton Conway, the Genius at Play - The New York Times

Kaynaklar
1) Dmitry Fuchs, Serge Tabachnikov, Mathematical Omnibus: Thirty Lectures on Classic Mathematics, American Mathematical Society, 2007.
2) T. C. Hales, Jordan’ s Proof of the Jordan Curve Theorem, Studies in logic, grammar and rhetoric 10, 45-60, 2007.
3) https://mathworld.wolfram.com/JordanCurve.html
4) https://en.wikipedia.org/wiki/Schoenflies_problem

Topolojik bir oluşum!

Tag Archives: Jordan eğri teoremi

Gözle Görülür Bir Gerçek, Asırlık Bir Bilmece: Jordan Eğri Teoremi

Patolojik Nesneler II- Alexander’ın Boynuzlu Küresi