Son patolojik nesnemiz, grup teoriden düğüm teorisine, oyun teoriden kodlama teorisine pek çok farklı alanda çalışmalar yapmış ve maalesef geçen sene Covid19 sebebiyle kaybettiğimiz efsane matematikçi John Horton Conway’den geliyor. Konuya girmeden önce, Conway’in Hayat Oyunu‘ndan (Game of Life) mutlaka bahsetmek gerekir. Çünkü daha önemli başarılara imza atmış olsa da, Conway birçok kişi tarafından Hayat Oyunu’nu bulan kişi olarak bilinir. O zaman, kendisi de bir hücresel otomat olan Hayat Oyunu’nu anlatmaya başlamadan önce, hücresel otomat nedir sorusuna cevap arayalım.

Düzlemde bir ızgara (grid) alalım ve bunun üzerindeki her bir hücrenin 0-1 ya da açık-kapalı gibi bir durumu olduğunu veya iki farklı renkten birine sahip olduğunu düşünelim. Yani örneğin;

ya da,

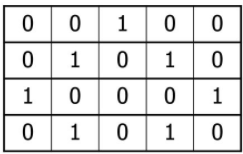
Ayrıca her hücrenin komşuları olduğunu varsayalım. Bu komşular farklı şekillerde tanımlanabilir fakat biz en genel haliyle, hücreye bitişik olan hücreleri onun komşuları olarak ele alabiliriz.

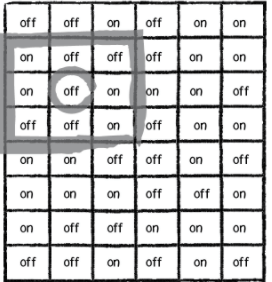
Şimdi elimizde bir başlangıç durumu olsun ve belli bir kural altında hücrelerin durumlarını değiştirerek yeni bir nesil (generation) elde edelim.

Örneğin yukarıdaki şekilde en soldaki resim başlangıç durumumuz olsun. Bir hücrenin komşularından en az dördü zıt renkteyse, o hücrenin renk değiştirdiğini kabul edelim. İşte bu kural altında sırasıyla yukarıdaki 2 yeni nesil elde edilir.

Yukarıda anlatılan bu sistemler hücresel otomatlar olarak adlandırılır. Hücresel otomat kavramı 1940’lı yıllarda Los Alamos Ulusal Laboratuvarı‘nda araştırmacı olan Stanisław Ulam ve John von Neumann tarafından ortaya koyulmuştur. Ulam’ın amacı kristallerin büyümesini modellemek iken Neumann’ın hayali kendini kopyalayan robotlardan oluşan bir dünyadır. Robotların bu işle alakası şu şekilde aslında. Izgara üzerinde bir desen belirleyin ve bu sizin tasarladığınız robot olsun. Bu desenin kendi kopyalarını oluşturmasına izin verecek kurallar dizisiyle robotumuzun bir kopyasını elde etmiş oluruz. İşte elde edilen bu yapı bir hücresel otomattır ve bir açıdan, biyolojik üremeyi ve hatta evrimi modelleyen bir süreçtir.

İşte Neumann’ın kendi benzerlerini üreten hücresel otomat fikri, bu yazının kahramanı olan Conway’in Hayat Oyunu isimli meşhur hücresel otomatının temeli olarak kabul edilebilir.

Hayat oyunu her hücrenin 8 adet komşuluğa sahip olduğu sonsuz bir ızgara (grid) üzerinde oynanır. Izgara üzerinde canlı ve ölü hücreler olduğunu düşünüp, bir sonraki nesilde hangi hücrelerin ölüp hangilerinin yaşamaya devam edeceğini belirleyen kurallara bir bakalım:

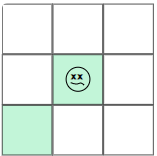
1) İkiden az canlı komşusu olan canlı bir hücre (yalnızlıktan) ölür. Örneğin aşağıdaki afallamış yeşil hücre, yalnızca 1 canlı komşusu olduğundan, bir sonraki nesilde ölecek.

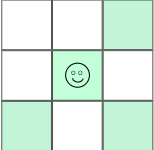
2) 2 ya da 3 canlı komşuya sahip olan canlı bir hücre, canlı kalmaya devam eder. Aşağıdaki şanslı velet gibi.

3) 3’ten fazla canlı komşusu olan canlı bir hücre (kalabalıktan) ölür. 4 canlı hücreye sahip olan aşağıdaki hücrenin ve belki de yakın bir gelecekte insanoğlunun başına geleceği gibi.

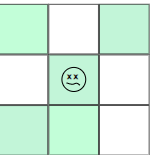
4) Tam olarak 3 komşusu olan ölü bir hücre, sonraki nesilde hayata döner. Yaşam sevinci ile dolu olan aşağıdaki ölü hücre gibi.

Oyun basit görünebilir ama altında yatan anlam çok derin. Çünkü yaşamın bilinçsiz basit hücrelerden, nasıl olup da bu kadar karmaşık hale geldiğinin bir göstergesi aslında.

Şimdi biraz da çoğu kişinin Hayat Oyunu ile tanıdığı ve 1960’lı yılların sonlarında tanımlamış olduğu Conway grupları ile yıldızı parlamaya başlayan John Horton Conway’in bu yazımıza konu olan ilginç fonksiyonundan bahsedelim.

İşe, bu fonksiyonun hangi duruma bir karşıt örnek olduğunu açıklayarak başlayalım. Bunun için önce, Analiz derslerinden aşina olduğumuz Ara Değer Teoremini hatırlayalım:

sürekli bir fonksiyon olsun. Bu durumda olacak şekilde her için olacak şekilde bir vardır. (İşimizi kolaylaştırmak adına, bu son kısmı ara değer özelliği olarak adlandıralım. Dolayısıyla teorem ” aralığı üzerinde tanımlı reel değerli her fonksiyon ara değer özelliğini sağlar” biçiminde olacaktır.)

Bu teoremin tersinin doğru olmadığı, yani ara değer özelliğini sağlayan ve kapalı sınırlı bir aralık üzerinde tanımlı olan reel değerli her fonksiyonun sürekli olması gerekmediğini biliyoruz. Örneğin;

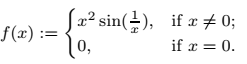
fonksiyonunu ele alalım. Bu fonksiyon üzerinde süreklidir. Bu nedenle Darboux Teoremi’nden türevi ‘de ara değer özelliğini sağlar. Fakat fonksiyonu noktasında sürekli değildir.

Aslında oldukça güzel bir örnek ama yine de biraz zayıf. Yani her yerde ara değer özelliğini sağlayan fakat yalnızca sonlu sayıda değil, hiçbir noktada sürekli olmayan bir fonksiyona sahip olsaydık, işte o zaman sezgilerimizi tamamen bir kenara bırakmak zorunda kalırdık. O halde şimdi bu özelliklere sahip olan ve Conway’in 13 tabanını kullanarak tanımlamış olduğu fonksiyona bir bakalım.

Bir sayıyı n tabanında yazmak için 0’dan n-1’e kadar olan rakamların kullanıldığını biliyoruz. Dolayısıyla, 13’lük sayma sisteminde kullanacağımız temel semboller, yani rakamlar, olacaktır. Şimdi 13 tabanında yazılmış 1056 sayısını ele alalım. Dikkat edersek burada şöyle bir karmaşa oluyor. Bu sayı 10-5-6 rakamlarından mı yoksa 1-0-5-6 rakamlarından mı oluşuyor? İşte bu karışıklıktan kurtulmak için, 10, 11 ve 12 rakamlarını, sırasıyla A, B ve C harfleriyle gösterelim. Conway orijinal çalışmasında A, B ve C yerine sırasıyla +,- ve . sembollerini kullanmış ve bunları 10’luk tabandaki versiyonlarından ayırmak için altlarını çizmiştir. (Yani örneğin + değil de + gibi.)

Artık fonksiyonunu tanımlamaya hazırız. Bunun için bir alalım ve ‘in 13 tabanında ondalık gösterimini yapalım. Burada ufak bir ayrıntı: Yazdığımız sayının sonsuz sayıda C ile bitmesine izin yok. Bu durumu 10’luk sistemde 0.99999… sayısına izin vermemek, bunun yerine 1’i kullanmak gibi düşünebiliriz. Şimdi olmak üzere, ‘in 13 tabanındaki gösterimi bir noktadan sonra formunda oluyorsa ; formunda oluyorsa ; bu iki durumdan hiçbiri sağlanmıyorsa olarak tanımlayalım. Burada fonksiyonunun çıktılarının 10 tabanında yazılmış sayılar olduklarını da eklemek gerekiyor. Bu fonksiyonu daha iyi anlayabilmek bazı noktaların altındaki görüntüsüne bakalım.

a) ‘in 13 tabanındaki gösterimi 14584A146C4546 olsun. Bu gösterim bir yerden sonra A146C4546 serisini içeriyor. O halde burada olur.

b) ‘in 13 tabanındaki gösterimi B4146C4ise olur.

c) ‘in 13 tabanındaki gösterimi 1C234A566 ise olur.

Conway’in 13 tabanında A, B ve C yerine +,- ve . kullandığından bahsetmiştik. Dikkat edersek fonksiyonu tanımlarken biz de bu sembollerin 10’luk sistemdeki versiyonlarını kullanıyoruz.

Yukarıda tanımlanan fonksiyonu her yerde ara değer özelliğini sağlayan bir fonksiyondur. Bunu göstermek için bir alalım ve olacak şekilde bir bulmaya çalışalım. İlk olarak ‘nin 10’luk tabandaki gösteriminde ondalık sayı noktasının olduğu yere C koyalım. Örneğin ise bunu ‘e dönüştürelim. Daha sonra bu sayının başına ise A ; ise B koyalım. Bu durumda r=-3.245’in son hali olacaktır. Burada olduğunu kolayca görebiliriz. Şimdi herhangi bir sayı olmak üzere, ‘nın sonuna eklemekle oluşan sayısı hem aralığındadır hem de özelliğini sağlar.

Diğer taraftan fonksiyonu hiçbir noktada sürekli değildir. Bir fonksiyonun bir noktasında sürekli olması, kabaca, ‘in civarındaki noktaların görüntülerinin de ‘in civarında olması anlamına gelir. Eğer fonksiyonu noktasında sürekli ise, bu noktada yerel sınırlı olmalı, yani ‘in civarındaki bir aralıkta sınırlı olmalıdır. (Burada sınırlılık olacak şekilde bir sayısının olması anlamına gelir.) Fakat fonksiyonumuz her açık aralığı için özelliğine sahiptir ve bu nedenle her noktası için, bu noktanın civarındaki tüm aralıklarda sınırsızdır.

Yine ufak bir örnek: 13 tabanındaki gösterimi olan reel sayısını ele alalım. Burada olacaktır. Bu sayıya oldukça yakın olan fakat görüntüsü ‘in yakınından bile geçmeyecek olan bir sayısı elde etmek mümkündür. 13 tabanında böyle bir sayısı elde etmek için şu adımları izleyelim:

(i) ‘e yakın bir sayı elde edebilmek için önce ‘in yanına birkaç tane 0 ekleyelim:
(ii) Yukarıda elde edilen sayının yanına, hesaplanırken bu kısmı tamamen geçersiz kılacak birkaç rakam/sembol koyalım:
(iii) (ii)’de elde edilenin sonuna değeri ‘in civarında olmayacak şekilde bir sayı dizisi getirelim: . İşte bu sayı ‘nin 13 tabanındaki gösterimi olmak üzere, olacaktır.
Bu hileyi her nokta için yapmak mümkün olduğundan, ‘nin hiçbir noktada sürekli olmadığını söyleyebiliriz.

Söz konusu matematik olduğunda, patolojik nesneleri anlatmakla bitiremeyiz. Çünkü aslında varlıklarına alıştığımız için bize tuhaf görünmeyen bile birçok patolojik nesne/durum var. Yani örneğin irrasyonel veya kompleks sayılar bu anlattıklarımızdan daha mı az patolojik sizce? Peki kenarları 1 birim olan ikizkenar dik üçgenin hipotenüsünün birim olması ya da (0,1) aralığı ile reel sayılar arasında bire-bir örten bir dönüşüm yazılabilmesi? Burada sadece üç örnekle bile zihnimizin sınırlarını zorlayan matematik sezgi dışı canavarlar üretmeye devam ediyor ve bizler var oldukça da devam edecek.

Kaynaklar
1) https://beltoforion.de/en/game_of_life/
2) https://plus.maths.org/content/maths-minute-cellular-automata
3) http://nebula2.deanza.edu/~karl/Sites/Bios/JohnConwayBio.pdf
4) https://www.youtube.com/watch?v=xKvX9hIPDbs
5) https://en.wikipedia.org/wiki/Conway_base_13_function
6) Greg Oman, The Converse of the Intermediate Value Theorem: From Conway to Cantor to Cosets and Beyond, Missouri J. Math. Sci. 26 (2), 134–150, 2014.