dizisel yakınsak | Topolojik bir oluşum!

Fonksiyonlar sadece matematiğin değil, farkında olmasak da günlük hayatımızın en önemli parçalarından biridir. Çünkü, karşılaştığımız sorunları çözmeye yardımcı olan karmaşık sistemler inşa etme özellikleriyle, sayısal dünyamızın temellerini oluştururlar. Soyut kavramları, üzerinde çalışabileceğimiz sayısal verilere dönüştürmemiz için bir yol sağlar, gerçek dünyadaki durumları matematiksel olarak modellememize yardımcı olurlar.

Özellikle matematikle ilgili bir eğitim alıyorsanız, muhtemelen içinde fonksiyonların olmadığı bir tek dersiniz bile olmayacaktır. Sürekli, türevlenebilir, harmonik, analitik, yakınsak, konveks, monoton, simetrik, integrallenebilir ve sınırlı olup olmadıklarını, olurlarsa bize ne gibi kolaylıklar sağlayacaklarını didikler durursunuz. Bu yazıda bahsedeceğim konu, makine öğrenmesinden görüntü işlemeye, kontrol teorisinden sinyal işlemeye kadar geniş bir kullanım alanına sahip olan fonksiyon dizileri ve bu dizilerin noktasal & düzgün yakınsaklıkları. Biliyoruz ki, matematikte bazı kavramlar (süreklilik, yakınsaklık, sınırlılık, integrallenebilirlik vs.) uniform yani düzgün versiyonlara da sahiptir. Sanırım çoğu zaman sıkıntı yaratan şey, bu ikisi arasındaki farkı anlamaktır. Yani bir fonksiyon dizisinin nereye yaklaştığını/yakınsadığını görmekte sıkıntı yaşamasak bile, bu yakınsamanın düzgün olup olmadığını tespit etmekte zorlanabiliriz. Öğrenmeye çalışmaktan bunalmışsanız, pes etmeden, bir deneme de birlikte yapalım.

Matematikte “dizi (sequence)” kavramıyla neyin kastedildiği konusunda aşağı yukarı bir fikir sahibiyseniz, fonksiyon dizilerinin, her bir bileşeni bir fonksiyon olan diziler olduğunu tahmin edebilirsiniz. Yani aslında $(f_n)_{n\in \mathbb{N}}=(f_1, f_2, f_3, \ldots )$ görünümünde bir şey. Şimdi soru şu: Tüm bu fonksiyonları çizebildiğimizi varsaysak, acaba $n\rightarrow \infty$ iken, dizinin spesifik bir $f$ fonksiyonuna yaklaştığını gözlemleyebilir miyiz? Daha matematiksel bir dille ifade etmek gerekirse, bu dizi yakınsak mıdır?

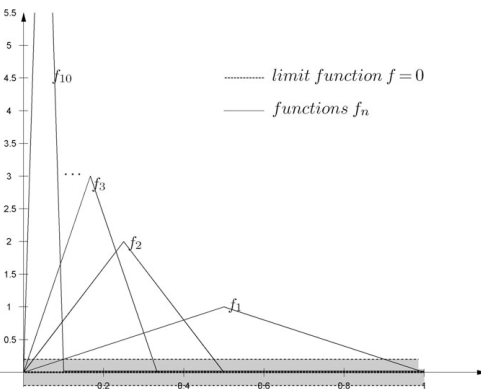
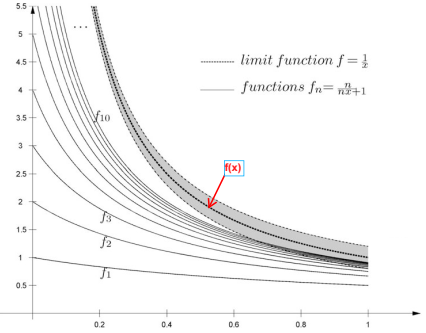
Yukarıdaki şekillerde verilen fonksiyon dizilerinde, $n\rightarrow \infty$ iken, dizinin yaklaştığı bir $f$ fonksiyonu olduğunu görmek mümkündür. Fakat biz burada yine tek bir yakınsama şekliyle yetinmeyecek ve farklı yakınsaklık türleri tanımlayacağız. İşe ilk olarak noktasal yakınsama kavramıyla başlayalım:

Öncelikle, $D\subseteq \mathbb{R}$ olmak üzere, $f_n: D \rightarrow \mathbb{R}$ fonksiyon dizisini ele alalım. Bu dizinin tanım kümesinden bir $a\in D$ noktası seçelim. Dikkat edersek, $({f_1}(a), {f_2}(a), {f_3}(a) \ldots )$ bir reel sayı dizisi olacaktır. Eğer her $x\in D$ için elde ettiğimiz sayı dizisinin yakınsadığı bir $f$ fonksiyonu bulabiliyorsak, yani $\forall x, \lim_{n\to \infty}{f_n}(x)=f(x)$ oluyorsa, ${f_n}$ dizisi $f$ ‘ye noktasal yakınsar (pointwise convergent) denir. Biraz daha teknik bir tanım vermek istersek,
$\forall x\in D, \forall \epsilon >0, \exists N \in \mathbb{N}$ if $n\geq N$ then $|{f_n}(x)-f(x)|<\epsilon$ .
Türkçesi şöyle: Rastgele bir $x$ seçelim. Şimdi bize verilecek her $\epsilon>0$ için, dizinin öyle bir $f_{N}$ terimi vardır ki, işte bu terimden sonra $|{f_n}(x)-f(x)|<\epsilon$ olur, yani ${f_n}(x)$ ile $f(x)$ arasındaki mesafe $\epsilon$ ‘dan küçüktür. Burada her $\epsilon>0$ seçiminin şöyle bir güzel yanı var: $\epsilon$ sayısını ne kadar küçültürsek küçültelim, $({f_n}(x))$ sayı dizisi N. terimden sonra $f(x)$ civarında kümelenmiş oluyor.
Seçilen her $x$ için bir $N \in \mathbb{N}$ bulabiliyoruz, ama bu $N$ sayısı seçilen her $x$ için aynı olmak zorunda değil. Yani örneğin $x=3$ için $({f_1}(3), {f_2}(3), {f_3}(3) \ldots )$ dizisi, 100. terimden sonra $f(3)$ ‘ün çevresinde yığılırken; $x=5$ için, 500. terimden sonra $({f_1}(5), {f_2}(5), {f_3}(5) \ldots )$ dizisi $f(5)$ sayısının etrafında yığılıyor olabilir. Burada aslında, farklı $\bf{x}$ değerleri için elde edilen sayı dizilerinin, limit fonksiyonuna varış hızlarının birbirinden farklı olduğunu söyleyebiliriz.

Bu kadar düzensizlik, efendime söyleyeyim her $\epsilon$ için farklı bir $N$ bulduğumuz yetmezmiş gibi, bir de her $x$ için farklı bir $N$ bulmak size de fazla kaotik gelmedi mi? O zaman şimdi, her bir noktada aynı hızla yakınsamayı garanti edecek yeni bir tanım inşa edelim. Her $\epsilon$ için, öyle bir $N$ sayısı bulalım ki, hangi $x$ noktasını denersek deneyelim, $f_{N}(x)$ sonrasındaki terimler $f(x)$ fonksiyonunun etrafında kümeleniyor olsun. Yani her $\epsilon$ ve her $x$ için iş görecek ortak bir anahtarımız olsun. İşte istenilen bu koşulu sağlayan bir $f(x)$ fonksiyonu varsa, ${f_n}$ dizisi $f$ ‘ye düzgün yakınsar (uniform convergent) denir ve
$\forall \epsilon >0, \exists N \in \mathbb{N}, \forall x\in D$ if $n\geq N$ then $|{f_n}(x)-f(x)|<\epsilon$
biçiminde ifade edilir. Dikkat edersek, düzgün yakınsaklık için öncelikle noktasal da olsa elimizde bir limit fonksiyonu bulmamız, daha sonra bu limit fonksiyonuna yakınsama hızı her noktada aynı mı değil mi diye bir test yapmamız gerekir. Şimdi birkaç örnek üzerinden bu kavramları anlamaya çalışalım ve düzgün yakınsaklığı kontrol edebileceğimiz yöntemleri inceleyelim.

1) $f_n: [0,1] \rightarrow \mathbb{R}, {f_n}(x)=x^n$ fonksiyon dizisini ele alalım. Öncelikle, noktasal bazda düşünüp, dizinin yakınsadığı bir $f$ fonksiyonu var mı, varsa nasıl tanımlı olmalıdır, onu anlamaya çalışalım. $x=0$ için ${f_n}(x)=0$ yani $({f_1}(0), {f_2}(0), {f_3}(0), \ldots)=(0, 0, 0, \ldots)$ ve bu dizinin limiti 0 olduğundan, $f(0)=0$ olmalıdır. $x=1$ için ise, ${f_n}(x)=1^n=1$ yani $({f_1}(1), {f_2}(1), {f_3}(1), \ldots)=(1, 1, 1, \ldots)$ ve bu dizinin limiti 1 olduğundan, $f(1)=1$ olmalıdır. $x\in (0,1)$ için, $\lim_{n \rightarrow \infty} x^n = 0$ olduğuna dikkat edelim. Bu durumda dizimizin
$f(x)= \begin{cases} 0 & x\in (0,1) \\ 1 & x=1 \\ \end{cases}$ fonksiyonuna noktasal yakınsadığını söyleyebiliriz.
Noktasal yakınsaklık cepteyse, şimdi de bu yakınsamanın düzgün olup olmadığını kontrol edebiliriz. Önce sezgisel olarak yorumlamaya çalışalım: Örneğin $x=\frac{1}{2}$ ve $x=1$ noktalarını ele alsak, bu iki nokta için, limit fonksiyonuna ulaşma hızlarının eşit olduğunu söyleyebilir miyiz? Tabii ki hayır, çünkü $x=\frac{1}{2}$ noktasında, dizimizin o noktadaki limite yani $f(x)=0$ ‘a ulaşmak için biraz çaba sarf etmesi gerekirken, $x=1$ noktasında bu çabaya gerek kalmaz. Çünkü zaten bu noktada dizimiz limit fonksiyonuna zaten eşittir. Dolayısıyla, yakınsamanın düzgün olmasını bekleyemeyiz.

Bunu doğrulamak için kullanacağımız yöntemlerden biri şöyle: Eğer her $n\in \mathbb{N}$ için ${f_n}$ sürekli ve yakınsama da düzgün ise, dizinin yakınsadığı $f$ fonksiyonu sürekli olmalıdır. Dolayısıyla eğer dizinin noktasal yakınsadığı $f$ fonksiyonu sürekli değilse, yakınsama da düzgün olmayacaktır. Yukarıdaki örnekte bulduğumuz $f(x)$ fonksiyonu sürekli olmadığından, yakınsama da düzgün değildir.

2) Düzgün yakınsamayı göstermek için kullanılan yöntemlerden bir diğeri de, $\lim_{n\to \infty} \text{sup}_{x\in D} |{f_n}(x)-f(x)|=0$ olduğunu göstermektir. Burada yapılan şey aslında, limit fonksiyonu ile dizideki fonksiyonlar arasındaki maksimum mesafenin sıfıra yaklaşıp yaklaşmadığını kontrol etmektir. Limit sıfır ise, yakınsama düzgündür. Şimdi bu yöntemi aşağıdaki örnekler üzerinde uygulayalım.

a) ${f_n}(x)=\frac{nx}{1+n^2 x^2}$ ( $x\in [0,1]$ ) fonksiyon dizisini ele alalım. İlk işimiz noktasal yakınsaklık araştırması yapmak olacak. Burada $x$ noktasının seçiminden bağımsız olarak, $\lim_{n\to \infty} \frac{nx}{1+n^2 x^2}= \lim_{n\to \infty} \frac{nx}{n(\frac{1}{n}+n x^2)}=\lim_{n\to \infty} \frac{x}{\frac{1}{n}+n x^2}=0$ olur. Demek ki dizimiz $f(x)=0$ fonksiyonuna noktasal yakınsar.
Peki bu yakınsama düzgün müdür? Eğer $f(x)=0$ fonksiyonu sürekli olmasaydı, cevabımız ‘hayır’ olacaktı. Fakat burada süreklilik olduğu için, bu yöntemden bir sonuç almak mümkün değil. O halde yukarıda verilen supremum (sup) yöntemini deneyelim. Bunun için, türev kavramı yardımıyla ${g_n}(x)=|{f_n}(x)-f(x)|=\frac{nx}{1+n^2 x^2}$ fonksiyonunun maksimum değerini bulmaya çalışalım:
${g_n}'(x)=0$ olacak şekilde $x$ değerlerini, yani fonksiyonun kritik noktalarını bulalım: ${g_n}'(x)=\frac{n-n^3x^2}{(1+n^2x^2)^2}=0$ ise $x=\pm \frac{1}{n}$ dir. Fakat üzerinde çalıştığımız aralık $[0,1]$ olduğundan, sadece $x= \frac{1}{n}$ noktasını kullanabiliriz. Şimdi ${g_n}'(x)$ ‘in $[0,\frac{1}{n}]$ aralığında pozitif, $[\frac{1}{n},1]$ aralığında negatif olduğunu gözlemleyelim. Bu durum, ${g_n}(x)$ ‘in $[0,\frac{1}{n}]$ aralığında artan, $[\frac{1}{n},1]$ aralığında ise azalan olduğu anlamına gelir.

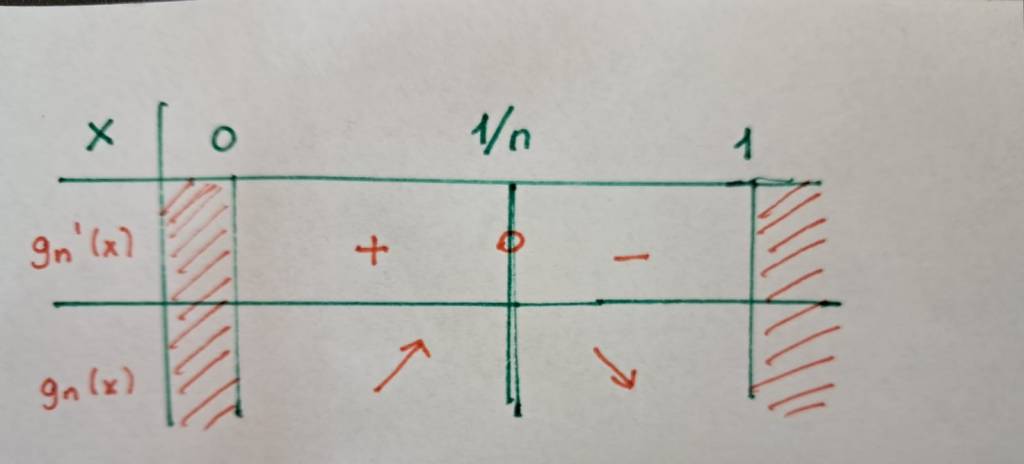
Elde ettiğimiz bu tablo bize, $x=\frac{1}{n}$ noktasında bir mutlak maksimum değeri olduğunu, yani $\text{sup}_{x\in [0,1]} |{f_n}(x)-f(x)| = {g_n}(\frac{1}{n})=\frac{1}{2}$ olduğunu söyler. Bu da aslında $\lim_{n\to \infty} \text{sup}_{x\in [0,1]} |{f_n}(x)-f(x)|\neq 0$ olması anlamına gelir. Demek ki buradaki yakınsama, düzgün değildir.

b) ${f_n}(x)=(x-\frac{1}{n})^2$ ( $x\in [-1,1]$ ) fonksiyon dizisini ele alalım. Burada yine, limit alma kuralları yardımıyla, $x$ noktalarının seçiminden bağımsız olarak, $\lim_{n\to \infty}{f_n}(x)=x^2$ olduğunu görebiliriz. Böylece fonksiyon dizimizin $f(x)=x^2$ fonksiyonuna noktasal yakınsadığını söyleyebiliriz. Sırada düzgün yakınsaklığı test etmek var. $|{f_n}(x)-f(x)|=|(x-\frac{1}{n})^2-x^2|=|\frac{1}{n^2}-\frac{2x}{n}| \leq \frac{1}{n^2}+\frac{2}{n}|x|$ ve $|x|\leq 1$ olduğundan $0\leq \text{sup}_{x\in [-1,1]} |{f_n}(x)-f(x)| \leq \frac{1}{n^2}+\frac{2}{n}$ olur. (Bu kısımda, supremum kavramını hatırlamak faydalı olacaktır.) Böylece, $\lim_{n\to \infty} \frac{1}{n^2}+\frac{2}{n}=0$ olduğundan, Sandviç/Sıkıştırma teoreminden, $\lim_{n\to \infty}\text{sup}_{x\in [-1,1]} |{f_n}(x)-f(x)|=0$ elde edilir. O halde, ${f_n}(x)$ dizisi, $f(x)=x^2$ fonksiyonuna düzgün yakınsar.

3) Sıradaki yöntemimiz, aşağıdaki koşulun sağlanıp sağlanmadığını kontrol etmek:

$\exists \epsilon_0 > 0 ; \forall n\in \mathbb{N}, \exists x_n \in D, |{f_n}(x_n)-f(x_n)|\geq \epsilon_0$

Burada amaç, $|{f_n}(x_n)-f(x_n)|\geq \epsilon_0$ olacak şekilde bir $\epsilon_0 > 0$ ve bir $x_n \in D$ dizisi bulmaya çalışmak. Şimdi bir örnekle anlamaya çalışalım.
${f_n}(x)=(\frac{n}{nx+1})$ ( $x\in (0,1)$ ) olsun. İlk aşama her zaman noktasal yakınsaklığın varlığını denetlemek. $\lim_{n\to \infty} \frac{n}{nx+1} = \lim_{n\to \infty} \frac{n}{n(x+\frac{1}{n})}=\lim_{n\to \infty} \frac{1}{x+\frac{1}{n}}=\frac{1}{x}$ . Demek ki fonksiyon dizimiz, $f(x)=\frac{1}{x}$ dizisine noktasal yakınsar.
Düzgün sürekliliği kontrol etmek için, $x_n=\frac{1}{n}$ ve seçersek, $|{f_n}(x_n)-f(x_n)|=|\frac{n}{n.\frac{1}{n}+1}-\frac{1}{\frac{1}{n}}|=|\frac{n}{2}-n|=\frac{n}{2}$ olduğundan $\epsilon_0=\frac{1}{2}$ için yukarıdaki koşulun sağlandığını görebiliriz. ( $n\in \mathbb{N}$ olduğunu kullanarak tabii.) Burada $x_n$ seçiminin nasıl yapıldığı meselesi biraz anlaşılmaz gelebilir. Tek bir atışın istenilen diziye isabet etmesini tabii ki bekleyemeyiz. Bir tam sayı elde etmemizi sağlayacak farklı $x_n$ dizileri deneyip, elde ettiğimiz tam sayıya göre bir $\epsilon_0$ seçimi yapmak, bu kuralı uygulamanın bir yolu olabilir.
Bir alıştırma olarak ${f_n}(x)=\frac{x}{n}$ $(x\in \mathbb{R})$ ve ${f_n}(x)=\frac{n^2 x}{n^4 x^2 +2} (x\in (0,1])$ dizilerinin noktasal yakınsak olduğu $f(x)$ fonksiyonunu bulup, düzgün yakınsak olmadığını da bu yöntemi kullanarak göstermeyi deneyebilirsiniz.

4) Şimdi de şu işin bir adını koyalım 😉 Yani şöyle isimli cisimli bir yöntem, ne bileyim, bir teorem filan kullanacağımız bir yol bulalım. Bunun için, $D$ kompakt bir küme olmak üzere, $f_n: D \rightarrow \mathbb{R}$ fonksiyon dizisi verilsin. Eğer,
(a) Her $n\in \mathbb{N}$ için $f_n$ süreklidir,
(b) $(f_n)$ dizisi $f$ fonksiyonuna noktasal yakınsar,
(c) üstelik bu $f$ fonksiyonu sürekli,
(d) ve hatta $f_n$ dizisi monotondur
koşulları sağlanıyorsa, $f_n$ dizisi $f$ ‘ye düzgün yakınsar der Dini Teoremi. Şimdi bu teoremi ${f_n}(x)=\frac{x}{x^2 +n^2} (x\in [0,1])$ dizisi üzerinde uygulamaya çalışalım. Her bir $f_n$ fonksiyonunun sürekliliği, $\lim_{n\to \infty} \frac{x}{x^2 +n^2}=0$ ve $f(x)=0$ fonksiyonunun sürekli olması ufak bir çabayla görülebilecek gerçekler. ${f_{n+1}}(x)=\frac{x}{x^2 +(n+1)^2} \leq \frac{x}{x^2 +n^2} ={f_n}(x)$ olduğundan monotonlukta da bir sorun yok. O halde, Dini teoreminden, yakınsamanın düzgün olduğu sonucunu çıkarabiliriz.

5) Şimdi biraz daha uçuk yöntemler peşinde koşacağız. Aşağıdaki teoreme bir bakalım:
Eğer $f_n: [a,b] \rightarrow \mathbb{R}$ fonksiyon dizisi (Riemann) integrallenebilir fonksiyonlardan oluşuyor ve $f$ fonksiyonuna düzgün yakıyorsa, $f$ de integrallenebilirdir ve $\lim_{n\to \infty} \int_a^b {f_n}(x) dx = \int_a^b \lim_{n\to \infty} {f_n}(x) dx = \int_a^b f(x) dx$ sağlanır. Yani limit ve integralin sırası değişebilir. Demek ki, integralin ve limitin sırası değişemiyorsa, yani yukarıda yazdığımız eşitlik sağlanmıyorsa, yakınsaklık düzgün olamaz.
O zaman bir örnek: ${f_n}(x)=2(n+1)x(1-x^2)^n (x\in [0,1])$ olsun. ${f_n}(0)={f_n}(1)=0$ dır. $x\in (0,1)$ olduğunda, $n\to \infty$ iken limit almaya çalışırsak, $0. \infty$ belirsizliğiyle karşılaşırız. Bu nedenle de L’ Hospital kuralı yardımıyla limiti 0 olarak buluruz. Demek ki dizimiz $f(x)=0$ fonksiyonuna noktasal yakınsar. Diğer taraftan $\int_0^1 2(n+1)x(1-x^2)^n dx= \left [ -(1-x^2)^{n+1} \right ]_0^1=1$ ve $\int_0^1 f(x) dx=0$ olduğundan, $\lim_{n\to \infty} \int_0^1 {f_n}(x) dx \neq \int_0^1 f(x) dx$ eşitliği sağlanmaz. O halde yakınsama düzgün olamaz.
Kendini denemek isteyenlere, bu yöntemi kullanabilecekleri bir örnek: ${f_n}(x)=\frac{2n^2 x}{(1+n^2x^2)^2}$ ( $x\in [0,1]$ ).

Düzgün sürekliliği göstermek için kullanılabilecek yöntemler bunlardan ibaret değil. Aşağıdaki yöntemler de mümkündür.
6) “her bir $f_n$ sınırlıysa ve $f_n$ dizisi $f$ ‘ye düzgün yakınsıyorsa, $f$ de sınırlıdır” teoremini kullanmak da bir teknik olabilir. Dizideki tüm fonksiyonlar sınırlı iken, noktasal yakınsadıkları $f$ fonksiyonu sınırlı olmuyorsa, yakınsama düzgün olamaz.
7) Düzgün Cauchy kriteri kullanmak ise diğer bir yol olabilir.
8) $f_n: [a,b] \rightarrow \mathbb{R}$ dizisi sürekli ve $f_n$ dizisi $f$ ‘ye düzgün yakınsıyorsa, “ $x_n \rightarrow x \Rightarrow {f_n}(x_n) \rightarrow f(x)$ özelliği sağlanır” teoremini kullanmak da mümkündür. $f_n$ fonksiyonları sürekli ve yani $x_n$ dizisi $x$ ‘e yakınsıyorken, $({f_n}(x_n))$ dizisi $f(x)$ ‘e yakınsamayacak şekilde bir $x_n$ dizisi bulabilirsek, yakınsama düzgün değildir. Örneğin ${f_n}(x)=nx^n(1-x)$ dizisini ele alalım. $x=0,1$ için ${f_n}(x)=0$ olduğundan $f(0)=f(1)=0$ ‘dır. $x\in (0,1)$ için, L’ hospital kuralı yardımıyla $\lim_{n\to \infty} {f_n}(x)= (1-x) \lim_{n\to \infty} \frac{n}{x^{-n}}= (1-x) \lim_{n\to \infty} \frac{1}{-x^{-n}ln(x)}=0$ elde edilir. Yani dizimiz, $f(x)=0$ fonksiyonuna noktasal yakınsar.
Diğer taraftan $x_n=\frac{n}{n+1}$ seçilirse, $(x_n)$ dizisinin 1’e yakınsadığı görülebilir. Fakat, ${f_n}(x_n)= {f_n}(\frac{n}{n+1})=n{(\frac{n}{n+1})}^n(1-\frac{n}{n+1})=\frac{n^{n+1}}{ (n+1)^{n+1}}=\frac{1}{(\frac{n}{n+1})^{n+1}}=\frac{1}{(\frac{n}{n+1})^n}\frac{n}{n+1}$ olduğundan $\lim_{n\to \infty} {f_n}(x_n)=\frac{1}{e}$ ‘dir yani, $({f_n}(x_n))$ dizisi $f(1)=0$ ‘a yakınsamaz. O halde, yakınsama düzgün değildir.

Burada detaylıca bahsettiğimiz yöntemlerden, özellikle ilk ikisi, en sık kullanılanlardır ve $\epsilon-N$ tanımına çok da girmeden işimizi halletmemizi sağlarlar. Son olarak şunu da unutmamak gerekir ki, çoğu konuda olduğu gibi, yakınsaklık konusunda da çözümün anahtarı, birçok örnek üzerinde çalışıp, tecrübe kazanmaktır.

KAYNAKLAR
1) Ludmila Bourchtein, Andrei Bourchtein, Theory of Infinite Sequences and Series, Birkhäuser, 2021.
2) https://people.math.wisc.edu/~angenent/521.2017s/UniformConvergence.html

Topolojik bir oluşum!

Tag Archives: dizisel yakınsak

Yakınsaklık vs Düzgün Yakınsaklık