CChebyshev metriği | Topolojik bir oluşum!

“The same equations have the same solutions” yani “Aynı denklemler aynı çözümlere sahiptir” demiş 20. yüzyılın tartışmasız en parlak beyinlerinden olan Feynman. Kendisinin Nobel ödüllü bir fizikçi oluşunu, ileri görüşlülüğünü, eşsiz mizahını, “Great Explainer” olarak bilinmesini sağlayan, en karmaşık fikirleri bile oldukça sade anlatabilme yeteneğini de göz önünde bulundurursak, yaptığı çıkarıma vereceğimiz tepki sanırım şöyle olur:

En karmaşık kavramları bile büyük bir sadelikle açıklayabilen Feynman’ın bu ilkesi, aldatıcı bir şekilde basit görünebilir. Fakat aslında bilimin ve evrenin birçok sırrını çözmenin anahtarıdır. İki fiziksel sistem aynı temel denklemler kümesiyle tanımlanabiliyorsa, aynı çözümleri veya sonuçları verecektir. Başka bir deyişle, farklı fiziksel olayların davranışları ve sonuçları, ortak bir matematiksel çerçeve kullanılarak anlaşılabilir ve tahmin edilebilir. Örneğin, Newton’un hareket yasaları, gezegenlerin güneş etrafındaki hareketlerini ve Dünya’daki nesnelerin davranışlarını tanımlamak için kullanılabilir.

Feynman’ın ifadesinin fiziğin ötesinde de sonuçları vardır. Örneğin matematikte soyutlama ve genellemenin gücünü ortaya koyar. Yani aslında, içinde yaşadığımız uzay ve bu uzayın belli kuralları varken, matematikçilerin neden metrik uzaylar, vektör uzayları, topolojik uzaylar gibi elle tutulmayan şeylerle uğraştıkları ve genelleme yaptıkları konusuna bir dayanak oluşturur. Tüm bunları anlamak için, matematikte uzay nedir, nasıl tanımlanır ve ne işe yarar sorularına yanıtlar bulmaya çalışalım.

Matematikte uzay tanımı galaksileri, yıldızları ya da kozmik fenomenleri içermez. Matematik dünyasında “uzay”, bir dizi eleman ve bu elemanlar arasındaki ilişkileri, davranışları tanımlayan bazı ek özellikler içeren matematiksel bir yapıdır. Bu yönüyle “küme” kavramından farklıdır. Çünkü uzayların bir iç yapılanması, yani elemanlar arasındaki ilişkilerin nasıl olacağının, yeni öğelerinin nasıl oluşturulacağının yazıldığı bir anayasası vardır. Örneğin;

Vektör uzayları, “vektör” adı verilen elemanları ve belli kurallara uyması gereken, toplama ve skaler çarpma işlemlerini içeren bir yapıdır.

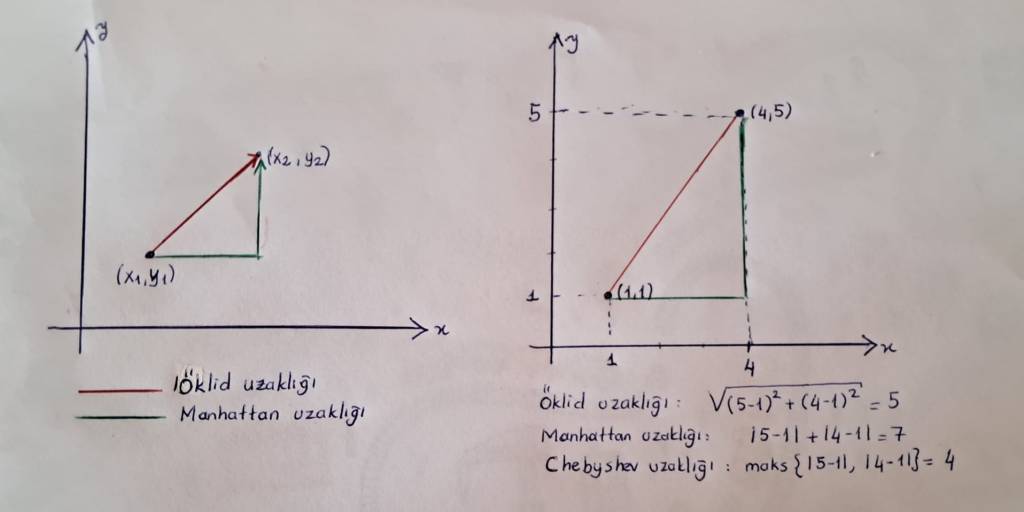
Metrik uzaylar, belli elemanlar ve bu elemanlar arasındaki mesafe kavramını tanımlayan metrik adında bir fonksiyon içeren bir yapıdır. Metrik dediğimiz, öyle “fonksiyonlar içinde bir fonksiyon” değildir. Negatif olmama, simetri özelliği ve üçgen eşitsizliği gibi bazı beklentilerimizi karşılaması gerekir. İşin ilginç yanı, bu uzaylarda mesafeyi ölçme meselesinin her zaman bir cetvel yardımıyla çözülememesidir.

Örneğin yalnızca dik hareketleri dikkate alan taksi metriğine göre $(x_1, y_1)$ ve $(x_2, y_2)$ gibi iki nokta arasındaki mesafe $|x_2-x_1|+ |y_2-y_1|$ formülüyle hesaplanır. Bu metrik Manhattan metriği olarak da adlandırılır, çünkü taksilerin sadece dik çizgiler boyunca seyahat edebildikleri ve kavşaklarda dik açılı dönüşler yapmak zorunda oldukları Manhattan sokaklarında hareket etme şeklini yansıtır.

Mesafeyi koordinatlar arasındaki maksimum fark olarak ölçen Chebyshev metriğine (maksimum metriği ya da $L_\infty$ metriği olarak da bilinir) göre ise $(x_1, y_1)$ ve $(x_2, y_2)$ noktaları arasındaki mesafe $\text{maks}\{ |x_2-x_1|, |y_2-y_1| \}$ olarak tanımlanır. Kurallara uyulduğu sürece, birçok farklı küme üzerinde birçok farklı metrik tanımlamak mümkündür.

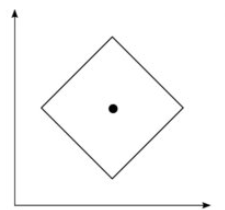
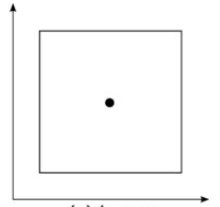
Farklı metrik uzaylarda, bildiğimiz tüm kavramların yepyeni bir anlam kazanacağına dikkat edelim. Örneğin, düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların kümesine çember denildiğini biliyoruz. “Uzaklık” tanımı değiştiğinde, çember dediğimiz şey de aynı formda kalmaya devam etmeyecektir. Bu nedenle $\mathbb{R}^2$ kümesi üzerinde taksi metriğine ve Chebyshev metriğine göre “çember” dediğimiz şey, sırasıyla, bir baklava dilimi ve bir kare görünümünde olacaktır.

Topolojik uzaylar, bir küme ve topoloji adı verilen bir ek yapıdan oluşur. Uzay tanımında bahsettiğimiz kurallar ise “topoloji” tanımında devreye girer. Topoloji, kümemizin alt kümelerinden oluşan ve bazı özel aksiyomları sağlayan bir küme ailesidir. Topolojik uzaylar, herhangi bir mesafeden bahsetmeyip, onun yerine “komşuluk” kavramını koyarak yakınlık kavramını incelemek için oldukça elverişli bir ortam sunar.

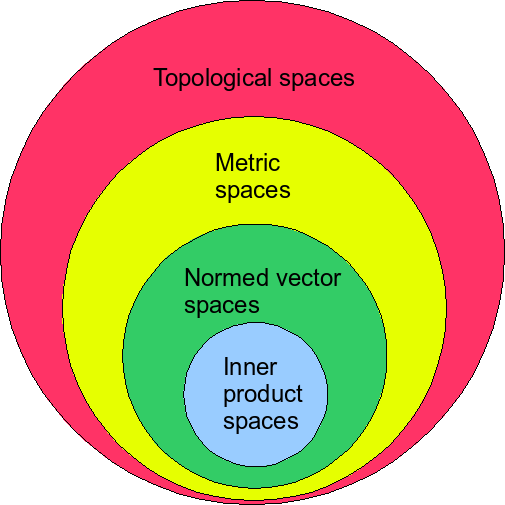
Bu listeyi oldukça genişletebilir (iç çarpım uzayları, normlu vektör uzayları, Banach uzayları, Hilbert uzayları vb.) ve hatta aralarındaki hiyerarşiyi farklı şekillerde resmedebiliriz.

Peki tüm bu genellemeleri nasıl yapıyoruz? Bunun için Feynman’ın, fizik yasalarını keşfetmek konusunu açıklarken başvurduğu satranç analojisine bir bakalım:

“Diyelim ki bir satranç oyunu. Oyunun kurallarını bilmiyorsunuz, ancak bazen en azından küçük bir köşeden tahtaya bakmanıza izin veriliyor. Bu gözlemlerden oyunun kurallarının ne olduğunu, taşların hareket kurallarının ne olduğunu anlamaya çalışıyorsunuz. Bir süre sonra, örneğin, tahtada sadece bir fil olduğunda, filin her zaman aynı renk üzerinde ilerlediğini keşfedebilirsiniz. Daha sonra filin bir diyagonal üzerinde hareket etmesine ilişkin yasayı keşfedebilirsiniz ve bu daha önce anladığınız yasayı, yani filin hareket ettiği karelerin renginin koruduğunu açıklar. Bu da bir yasayı keşfedip daha sonra onu daha derin bir şekilde anlamamıza benzer.“

İşte matematiksel genelleştirmeler yapmak ve yeni soyut uzaylar tanımlamak da bir anlamda buna benzer. Fizik kanunlarını keşfetmenin, basit gözlemlerden derin teorilere doğru ilerlemeyi gerektirmesi gibi, matematik de giderek soyutlaşan kavramları keşfetmeye ve bu kavramların uyumlu bir şekilde iç içe geçtiği alanları tanımlamaya çalışır. Örneğin 3-boyutlu uzayda, mesafe dediğimiz şeyin pozitif olduğu, noktalar arası uzaklığın simetrik olduğu (yani, $x$ ile $y$ ‘nin birbirine olan uzaklığı ile $y$ ile $x$ ‘in uzaklığının aynı şey olduğu) gibi gözlemler yaparsınız. Daha sonra bunu, bir genelleme yaparken, yani metrik uzayların yasalarını tanımlarken kullanırsınız. Tıpkı gözlemcinin, fillerin beklenen davranışlarına dayalı bir zihinsel modele sahip olması gibi, matematikçiler de genellikle gözlemlenen örüntülere veya özelliklere dayanarak genelleştirilmiş uzayların zihinsel modellerini geliştirirler.

“Sonra bir şeyler olabilir -her şey yolunda gidiyor, tüm yasalara sahipsiniz, çok iyi görünüyor- ve sonra aniden bir köşede garip bir fenomen ortaya çıkar. Bu yüzden bunu araştırmaya, aramaya başlarsınız. (…) Uymayan şey, en ilginç olan şeydir, beklediğiniz gibi gitmeyen kısımdır. Ayrıca, fizikte devrimler de olabilir. Fillerin renklerini koruduğunu ve köşegenler boyunca ilerlediğini fark ettikten ve herkes bunun doğru olduğunu bildikten sonra, bir gün aniden bir satranç oyununda filin rengini korumadığını, değiştirdiğini keşfedersiniz.“

Şimdi, yerleşik düzene uygun sayısız oyundan sonra, bir filin ilerlediği karenin renginin değiştiği bir satranç oyunuyla karşılaştığınızı hayal edin. Bu beklenmedik olay, fil hareketlerinin genelleştirilmiş uzayına ilişkin anlayışınıza meydan okur. Matematiksel açıdan bu benzetme, genelleştirilmiş bir uzayda istisnalar veya varyasyonlarla karşılaşmak gibidir. Bunun üzerine, bu istisnai durumu da içeren yeni bir uzay tanımlarsınız.

Son olarak matematikte genelleştirmeler yapmanın avantajlarından bahsedelim.

“Birçok farklı fiziksel durum için denklemler tamamen aynı görünüme sahiptir. Elbette semboller farklı olabilir – bir harf diğerinin yerine kullanılır – ancak denklemlerin matematiksel biçimi aynıdır. Bu, bir konu üzerinde çalıştıktan sonra, başka bir konunun denklemlerinin çözümleri hakkında doğrudan ve kesin bilgiye sahip olduğumuz anlamına gelir.” diyor Feynman.
Demek ki yeni uzaylar tanımlama yoluyla genelleştirmeler yapmak, bir alandaki kanıtların diğer birçok alana uygulanabilir olmasını sağlar. Feynman’ın da bahsettiği gibi, semboller, isimler tamamen farklı olsa da, problemimiz aslında var olan bir teorinin bir parçası olabilir. Örneğin kalıcı homoloji (persistent homology) sayesinde, cebirsel topolojide bulunan teoremleri ve sonuçları, yüksek boyutlu verileri analiz etmek ve yorumlamak için kullanabiliriz.
Şehirlerin düğüm (node), yolların da kenar (edge) olduğu karmaşık bir ulaşım ağı düşünün. Bu problemi, düğümlerin konumları, kenarların ise bağlantıları temsil ettiği bir çizge (graph) olarak ele alıp, çizge teorisinde bulunan araçlar yardımıyla rotaları optimize edebilir, en kısa yolları bulabiliriz. Bunun dışında, sosyal ağlar, makine öğrenmesi, kriptografi gibi birçok alanda ortaya çıkan problemleri de çözebiliriz.
Lineer cebirde, vektör uzaylarından gelen kavramları ve tekil değer ayrışımı (SVD) gibi teknikleri, görüntü sıkıştırma teknolojisinde kullanabiliriz. Bu soyutlama sayesinde, görsel bir sorunu matematiksel bir soruna dönüştürerek verimli sıkıştırma yöntemleri elde etmiş oluruz.

Soyut uzaylar bazı temel özellikleri koruyarak çok sayıda sorunu çözmemizi sağlar. Akışkanlar dinamiğiyle uğraşan bir mühendis, yüksek boyutlu verilerdeki örüntüleri inceleyen bir veri bilimciyle aynı ilkeleri kullanabilir. Matematikte uzayların ve genelleştirmelerin güzel olmaları, yalnızca matematiksel zarafetlerinden değil, aynı zamanda disiplinler arasında bir köprü olma potansiyellerindendir.

KAYNAKLAR

Topolojik bir oluşum!

Tag Archives: CChebyshev metriği

Feynman’ın Perspektifinden Matematik: Uzaylar ve Genelleştirmeler