Öyle bir çağda yaşıyoruz ki, üzerine belki yüzlerce insanın kafa yorduğu ve tüm hayatlarını adadıkları sorular bizler için sadece sıradan ve kanıksanmış birer gerçek. Örneğin Dünya’nın şekli. Dünya’nın yuvarlak olduğu fikrinin izlerini sürdüğümüzde ilk olarak Pisagor ile karşılaşıyoruz. Hatta ondan sonra gelen Pisagorculardan, Dünya merkezli evren teorisini terk edenler bile vardır. Aristo da Dünya’nın küre olduğunu düşünenlerdendir ve Büyük İskender’in özel öğretmeni olması fikirlerinin yayılmasına katkıda bulunmuştur. Dünya’nın küre olduğu fikrinden yararlanarak çevresini ölçen Eratosthenes ise şaşırtıcı derecede yakın bir değer bulmuştur.
Dünya üzerinde bir noktadan sürekli batıya gidip en sonunda başladığımız yere dönmüş olmak, bize onun küre oluşu hakkında kesin bir bilgi verir mi? Belki de Dünya bir torus (simit) şeklindedir ve Macellan ile mürettebatı torusun iç ya da dış halkası boyunca dolaşmışlardır. Dünya’dan ayrılıp fotoğrafını çekme gibi bir imkanımız olmasaydı ya da Venüs gibi bulutlarla kaplı bir gezegenimiz olsaydı (ki bu durumda, bir torusun iç kısmında yaşıyor olsak, yukarı baktığımızda yüzeyin diğer kısmını göremezdik) Dünya’nın şekli üzerine bir yorum yapabilir miydik?

Sorumuza yanıt ararken bazı topolojik kavramlara ihtiyacımız olacak.
Elimizdeki nesneyi çekerek, uzatarak fakat sürekliliği bozmadan (yani yırtmadan) diğer bir nesneye dönüştürebiliyorsak bu iki nesnenin topolojik olarak eş yapılı, yani birbirlerine homeomorfik olduklarını söyleyebiliriz. Buna verilebilecek en klasik örnek bir donut (yani katı torus) ile kupanın topolojik olarak eş yapılı olmasıdır.

Bir n-manifold, her noktası n-boyutlu Öklid uzayına homeomorfik olan bir komşuluğa sahip olan bir topolojik uzaydır. Örneğin küre yüzeyi bir 2-manifolddur ve küre yüzeyinde yürüyen biri kendini bir düzlem üzerinde yürüyor sanır. Katı bir top bir 3-manifold, çember ise 1-manifolddur. Yani aslında boyut, elimizdeki nesnenin sığacağı boyut sayısı değil, o nesne üzerinde gezen birinin deneyimleyebileceği bağımsız yönlerin sayısıdır.
İki manifoldun bağlantılı toplamını elde etmek için her bir manifolddan birer disk kesip çıkarırız ve bu dairelerin sınır çemberlerini birbirine yapıştırırız. Aşağıdaki şekilde iki tane torusun bağlantılı toplamı ile iki delikli bir torusun nasıl elde edildiğini görebiliriz.
Herhangi bir manifold ile bir kürenin bağlantılı toplamı yine aynı manifoldu verecektir. Küreden bir disk çıkarıldığında elimizde yine bir disk kalır. Dolayısıyla bağlantılı toplamı elde etmek, bir diski çıkarıp yerine başka bir disk koymakla aynı şeydir.
Peki yönlendirilemez manifold ne demektir? Kendimize manifold üzerinde bir başlangıç noktası belirleyip seyahate başlayalım. Bu noktaya geri döndüğümüzde baş aşağı yani tepetaklak duruyorsak üzerinde bulunduğumuz manifold yönlendirilemez bir manifolddur. Yani tam olarak şöyle:
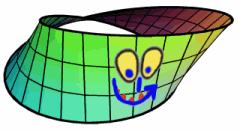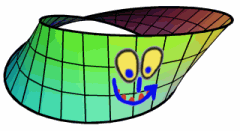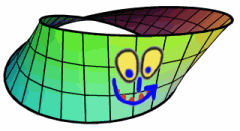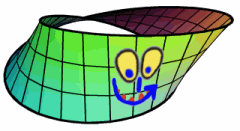
https://plus.maths.org/content/imaging-maths-inside-klein-bottle-2
Fakat bir çember veya torus üzerinde yürürken böyle bir durumla karşılaşmayız, bu nedenle çember ve torus yönlendirilebilir manifoldlardır.
Bir manifoldun sınırı, o manifoldun kenarı ya da kenarlar topluluğudur. Örneğin bir çemberin sınırı yoktur fakat çember, bir dairenin sınırıdır. Aynı şekilde bir kürenin sınırı yoktur (ki bu aynı zamanda küreden düşemeyeceğimiz anlamına da gelir), fakat küre katı bir topun sınırıdır. Genel olarak bir n-manifoldun boyutu n-1 olacaktır.
Bu bilgiler ışığında Dünya’nın sonlu, sınırı olmayan ve yönlendirilebilir bir 2-manifold olduğunu söylemek mümkündür. Bu durumda yüzeylere ilişkin sınıflandırma teoreminden, bir küre, ya da n-delikli () bir torus üzerinde yaşıyor olabileceğimiz sonucuna ulaşırız. Peki n-torus biçiminde bir Dünya teorisini nasıl çürütebiliriz, yani bir torus ile küreyi birbirinden ayıran şey nedir? Bunun için, yüzey üzerindeki kapalı yolları yani başlangıç ve bitiş noktası aynı olan yolları ele alalım. Yüzeyde kapalı bir yol üzerinde seyahat ederken peşimizden bir ip saldığımızı hayal edelim. Tabii ipi başlangıç noktasında bir yere bağlamayı ihmal etmiyoruz ve dönüşte de iki ucu birbirine bağlayıp kapalı bir şekil oluşturuyoruz. Soru şu: İpimizi, yüzeyden hiç ayırmamak kaydıyla tek bir noktaya büzebilir miyiz? Cevabımız evetse yani manifold üzerindeki her döngüyü, bir noktaya sürekli bir şekilde büzmek mümkünse, o manifoldun basit bağlantılı olduğunu söyleyebiliriz. Aşağıdaki şekiller yardımıyla da kolayca görebileceğimiz gibi küre basit bağlantılı iken torus değildir. (Dikkat edersek torusun sol tarafında yer alan çemberi tek bir noktaya büzmek mümkün değildir.)

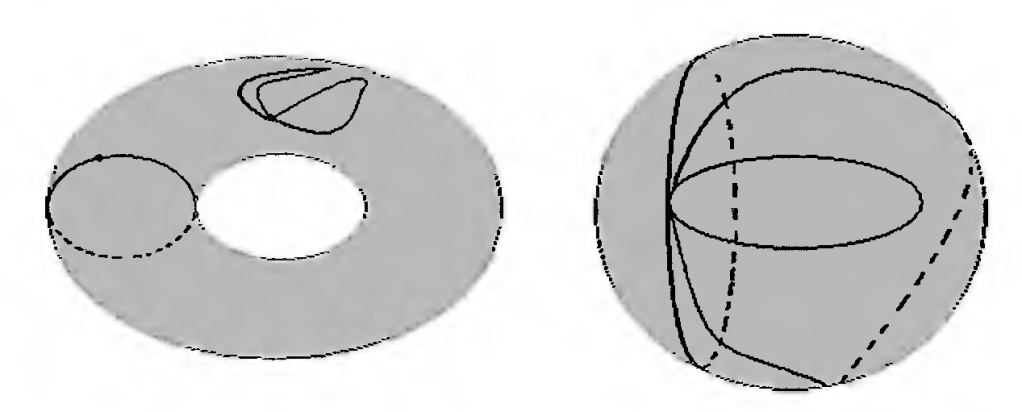
O halde Dünya’nın şekline dair elimizde sadece küre seçeneği kalıyor. (Torus olduğuna inananlar yok mu diyenler ve yeni teorilere yelken açmak isteyenler buraya.)
2 boyutlu manifoldlardan yararlanarak Dünya’nın şekli hakkında bir yorum yapılabileceğini gördük. Evrenin şekli hakkında tahminlerde bulunmak için ise 3 boyutlu manifoldlara ihtiyaç duyulacağı çıkarımını yapabiliriz. Tabii gözlenebilir Evren‘in bile çok ufak bir kısmından haberdar olduğumuzu göz önünde bulundurursak, bu işin öyle kolay olmayacağını anlayabiliriz. Yine de neler olup bitiyor bir göz atmak isteyenler için:
https://www.americanscientist.org/sites/americanscientist.org/files/200522415348_306.pdf
https://my.vanderbilt.edu/stacyfonstad/files/2011/10/ShapeOfSpace.pdf
Kaynaklar
1) Donal O’Shea, Poincare Sanısı / Geometri, Topoloji ve Evrenin Şekli, TÜBİTAK yayınları, 2017.
2) http://www.math.brown.edu/tbanchof/Yale/project15/math.htm
