asal sayılar sonsuzdur | Topolojik bir oluşum!

Asal sayıların sonsuz olduğunu gösterirken, genelde aklımıza gelen şu ispat oluyor:

Tersine, asal sayıların sonlu olduğunu kabul edelim ve tüm asal sayıların kümesini $P=\{p_1, p_2, \ldots, p_r\}$ ile gösterelim. $p=p_1 p_2\ldots p_r+1$ olsun. Varsayıma göre $p$ asal olamaz, o halde $p$ ‘nin bir q asal böleni vardır. Ayrıca $q\notin P$ ‘dir, çünkü aksi halde q’nun $p-( p_1 p_2\ldots p_r)=1$ ‘i bölmesi gerekir, ki bu bir çelişkidir. O halde asal sayılar sonsuz olmalıdır.

Çoğu yerde yazanın aksine, bu ispat aslında Öklid’in orijinal ifadesinden farklıdır. Çünkü M.Ö. 330-275 yılları arasında yaşamış olan Öklid’in, şuan gayet doğal kavramlar olarak görülen tamsayıları, bölünebilmeyi ve sonsuzu bizler gibi anlayıp ifade etmesini bekleyemeyiz.

Günümüzdeki yaklaşımdan farklı olarak, Antik Yunan’da tam sayıları soyut nesneler olarak değil, birimlerin sayısı olarak algılamışlar ve doğru parçalarının uzunlukları ile temsil etmişlerdir. Öklid, orijinal ispatta bölünebilme yerine “ölçme” ifadesini kullanmış ve bunu “a uzunluğundaki doğru parçalarının belli sayıdaki toplamı b’ye eşitse, a uzunluğu b’yi ölçer” şeklinde açıklamıştır. Önermenin orijinal ifadesi ve ispatı şöyledir:

Asal sayıların miktarı, belirlenmiş herhangi sayıda asal sayıdan daha fazladır.

İspat: A,B ve C asal sayılar olsun. A,B ve C’den daha fazla asal sayı olduğunu iddia ediyorum. A, B ve C ile ölçülen en küçük sayı olan DE’yi ele alalım. Daha sonra DE’ye DF birimini (yani, bir birim uzunluktaki doğru parçasını) ekleyelim.

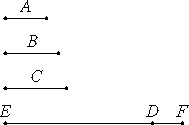
EF ya asaldır ya da değildir. İlk olarak asal olduğunu kabul edelim. Bu durumda, A, B, ve C’den daha fazla asal sayı bulmuş olduk. Şimdi de EF’nin asal olmadığını kabul edelim. Bu durumda EF, bazı asal sayılarla ölçülecektir. Diyelim ki EF, G asal sayısı ile ölçülsün. G’nin A, B ve C sayılarından farklı olduğunu iddia ediyorum. Diyelim ki G, bunlardan biriyle aynı olsun. Bu durumda G, DE’yi ölçer. Fakat aynı zamanda EF’yi de ölçtüğünden, DF’yi de ölçmelidir, ki bu saçma bir şeydir. Bu nedenle G; A, B ve C sayılarından herhangi biriyle aynı değildir ve hipoteze göre asaldır. Bu durumda yine, A, B ve C’den daha fazla asal sayı bulmuş olduk.

Bu önermenin birkaç farklı ispatı daha mevcut, fakat burada anlatacağım, Hillel Furstenberg’in 1955 yılında topolojik uzayları kullanarak yapmış olduğu ilginç ve bir o kadar da güzel ispat.

Bunun için öncelikle $\mathbb{Z}$ üzerinde bir topolojik uzay tanımlayacağız. $a,b\in \mathbb{Z}$ ve $b>0$ olmak üzere, $N_{a,b}=\{a+nb : n\in \mathbb{Z}\}$ kümesini tanımlayalım. Şimdi bu kümeyi biraz daha yakından tanıyalım. Bunun için bir $a$ tamsayısı alalım ve bu $a$ sayısından başlayarak, pozitif ve negatif yönde sürekli $b$ birim ilerleyelim. Böylece $N_{a,b}=\{a, b, -b, 2b, -2b, 3b, -3b,\ldots\}$ olacaktır. Ayrıca kümenin tanımından, her $x\in N_{a,b}$ için $N_{x,b}=N_{a,b}$ olduğu da söylenebilir. Şimdi,

$\tau =\{\emptyset\}\cup \{O\subseteq \mathbb{Z} : \forall a\in O, \exists b>0 ; N_{a,b}\subseteq O\}$

olmak üzere, $(\mathbb{Z}, \tau)$ ‘nun bir topolojik uzay olduğunu gösterelim:

$\emptyset, \mathbb{Z} \in \tau$ ve ayrıca açık kümelerin keyfi birleşiminin açık olduğu tanımdan kolayca görülüyor. O halde, $O_1,O_2 \in \tau$ alalım ve keşisimlerinin açık olduğunu görelim. Bu kümelerden en az biri boş küme ise, kesişimleri boş küme olacağı için açıktır. $O_1\neq \emptyset$ , $O_2\neq \emptyset$ olduğunu kabul edelim ve $x\in O_1\cap O_2$ alalım. Bu durumda, $x\in N_{a_1,b_1}\subseteq O_1$ ve $x\in N_{a_2,b_2}\subseteq O_2$ olacak şekilde $a_1,b_1,a_2,b_2 \in \mathbb{Z}$ vardır. Ayrıca yukarıda da belirttiğimiz gibi, $N_{x,b_1}= N_{a_1,b_1}$ ve $N_{x,b_2}= N_{a_2,b_2}$ olduğundan, $x\in N_{x,b_1 b_2}\subseteq N_{x,b_1}\cap N_{x,b_2}\subseteq O_1\cap O_2$ ve böylece $O_1\cap O_2\in \tau$ ‘dir.

Bu uzayda;
(i) Boştan farklı her açık küme sonsuz bir kümedir.
(ii) Her $N_{a,b}$ kümesi kapalıdır.

Birinci iddia tanımdan gayet açık. İkincisi için ise $N_{a,b}=\bigcup_{k=1}^{b-1} N_{a+k,b}$ eşitliği sağlandığından, $N_{a,b}$ kapalı bir kümedir diyebiliriz. (Çünkü $N_{a,b}$ , açık bir kümenin tümleyenidir.)

Şimdi bu topolojiyi kullanarak asal sayıların sonsuzluğunu gösterelim.

$\mathbb{P}$ asal sayıların kümesi olmak üzere, $\mathbb{Z}\setminus\{-1,1\}=\bigcup_{p\in \mathbb{P}} N_{0,p}$ eşitliği sağlanır. Çünkü her $x\in \mathbb{Z} \setminus \{-1,1\}$ sayısının bir $p$ asal böleni olduğundan $x\in N_{0,p}$ olur.

Eğer $\mathbb{P}$ sonlu olsaydı, (ii) özelliğinden, $\bigcup_{p\in \mathbb{P}} N_{0,p}$ kapalı kümelerin sonlu birleşimi olarak kapalı bir küme olurdu. Bu durumda $\{-1,1\}$ kümesi açık bir küme olur, ki bu durum (i) özelliği ile çelişir. Demek ki, $\mathbb{P}$ sonsuz olmalıdır.

Kaynaklar
(1) Aigner, Martin; Ziegler, Günter M. (1998). “Proofs from The Book”. Berlin, New York: Springer-Verlag.

Topolojik bir oluşum!

Tag Archives: asal sayılar sonsuzdur

#asalsayılarsonsuzdur #topolojiheryerde