Bu yazıda, bir önceki yazıda öğrenmiş olduğumuz kavramların da yardımıyla, Gödel’in Eksiklik Teoreminin olabildiğince sadeleşmiş bir ispatına yer vereceğiz. Ayrıca bu teoremin çözümünün başka hangi reaksiyonları tetiklediğini, ve bizleri, zihnimizin sınırlarını zorlar boyutta, ne tür problemlerle baş başa bıraktığını da göreceğiz. Hazırsak, başlayalım.
İlk olarak, doğal sayılar aritmetiğini kapsayan bir formal sistem bir ele alalım. Burada formal sistemden kastımız, simgeleri ve kuralları kesin olarak tanımlanmış bir sistemdir. Örneğin tüm sembolleri, bağlaçları ve kuralları ile önermeler mantığı bunun güzel bir örneğidir. Ele aldığımız bu sistemi, Alfred North Whitehead ve Bertrand Russell’ın Principa Mathematica’sından ilham alarak PM ile gösterelim, ve PM’nin, temel matematiksel gerçekleri ispatlamaya olanak veren bir sistem olduğunu kabul edelim. (Burada, Principa Mathematica’nın amaçlarından birinin, az sayıda mantıksal önermeden matematiğin tüm temel önermelerini çıkarmak olduğunu hatırlamak önemlidir.)
Gödel ilk olarak her sembole, her formüle (yani semboller dizisine) ve her kanıta bir doğal sayı karşılık getirilebileceğini göstermiştir. Her sembolün, formülün ya da kanıtın bir etiketi gibi düşüneceğimiz bu sayıya, sembolün/formülün/kanıtın “Gödel sayısı” denir. Öncelikle bu numaralandırma sisteminin nasıl olduğuna biraz açıklık getirelim. İlk olarak 12 temel sembolün Gödel sayıları, aşağıdaki tablodaki gibi verilmiş olsun.
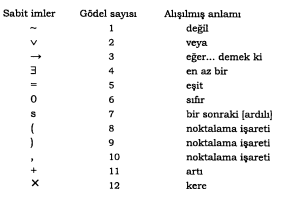
Bunların yanı sıra;
- x, y ve z ile başlayan değişkenlerin Gödel sayıları 12’den büyük asal sayılar,
- önerme değişkenleri, 12’den büyük asal sayıların karesi,
- yüklem değişkenleri (predicate variables), 12’den büyük asal sayıların küpü ile numaralandırılmış olsun.



Şimdi de PM’deki formüllerin Gödel sayılarının elde ediliş yöntemini bir örnekle anlamaya çalışayım. , yani “x, y’nin ardılı olacak şekilde bir x vardır” formülünü ele alalım. Yukarıda verilen tabloları kullanarak, her bir sembole ilgili Gödel sayısını karşılık getirelim:
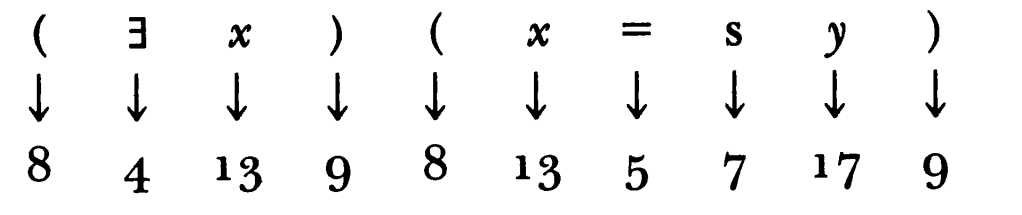
Bu formülün Gödel sayısını elde etmek için, asal sayıları büyükten küçüğe dizelim ve yukarıda elde ettiğimiz sayılar dizisinin elemanlarını, sırasıyla bu asal sayıların bir üssü olarak yazalım. Bu durumda formülümüzün Gödel sayısı tüm bu üslü sayıların çarpımı, yani olacaktır. Diğer taraftan,
, yani “2, 3’e eşit değildir” formülünün Gödel sayısını bulmak için, önce bu formülü,
biçiminde ifade etmemiz, daha sonra yukarıdaki gibi hesaplamamız gerektiğini unutmayalım.
Son olarak, ispat yaparken karşımıza çıkabilecek olan formül dizilerine karşılık gelen Gödel sayısının nasıl bulunabileceğini, yine bir örnek yardımıyla anlamaya çalışalım. “y’nin en az bir ardılı vardır.”
“0’ın en az bir ardılı vardır. “
formül dizisini ele alalım. Bu iki ifadenin bir formül dizisi oluşturmasının sebebi, ikinci formülün, birincide yerine 0 koymakla elde edilmiş olmasıdır. İlk formülün Gödel sayısının m, ikincisinin ise n olduğunu kabul edersek, bu formül dizisine karşılık gelen Gödel sayısı
olacaktır. Burada yaptığımız şey, aslında, her bir formülün Gödel sayını, küçükten büyüğe doğru sıralanmış asal sayıların üstlerine sırasıyla yazmak, sonrasında elde edilen bu sayıları çarpmaktır.
Yukarıda, her bir formüle karşılık gelen Gödel sayısını nasıl bulabileceğimizden bahsetmiştik. Bu işlemin tersinin, yani verilen herhangi bir sayıyı çözümleyip, bunun bir formülün Gödel sayısı olup olmadığını, eğer öyle ise, hangi formüle karşılık geldiğini bulmanın da mümkün olduğunu söyleyebiliriz. Örneğin 243000000 sayısını ele alalım. biçiminde yazılabilir. Asal sayıların üslerine (6-5-6) karşılık gelen sembolleri yazarsak,
formülünü elde ederiz.
Gödel tüm bunların yanı sıra üst-matematiksel (meta-mathematical) önermeleri de, içerisinde doğal sayıların birbirleriyle ilişkilerini barındıran özelliklere dönüştürmüştür. Şimdi ilk olarak, matematiksel ve üst-matematiksel arasındaki farkın ne olduğunu anlamaya çalışalım. Bunun için 2+3=5 önermesini ele alalım. Bu önerme matematiğe aittir. Fakat, bize bu önerme ile ilgili bilgiler veren “2+3=5 bir matematik formülüdür” ya da “2+3=5 eşitliği doğru değildir” ifadesi üst-matematiksel bir önermedir.
Peki, örneğin “ formülünün ilk sembolü
‘dir.” üst matematiksel önermesini PM aritmetiğinde nasıl ifade edebiliriz? Öncelikle
önermesinin Gödel sayısının
olduğunu kolayca görebiliriz. Bu durumda, “2, a’nın bir çarpanıdır, fakat
değildir” ifadesi,
‘nın
ile başladığı anlamına gelir. Ayrıca,
‘nin Gödel sayısı 1 olduğundan, bu ifade aslında,
önermesinin ilk sembolünün
olduğu anlamına gelir. Diğer taraftan, “x, y’nin bir çarpanıdır” demek, “
demektir. Dolayısıyla “2,
‘nın bir çarpanıdır, fakat
değildir” ifadesinin PM diline çevirisi şu şekilde olacaktır:
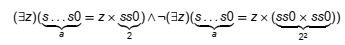
Yani, olacak şekilde bir
vardır ve
olacak şekilde bir
yoktur.
Gödel’in ispatına girmeden, sonradan ihtiyacımız duyacağımız birkaç gösterimden bahsetmemiz gerekir.
- dem(x,z) : “Gödel sayısı
olan bir formüller dizisi, Gödel sayısı
olan bir formülün PM içerisindeki bir kanıtıdır.” üst-matematiksel ifadesini ele alalım. Bu ifadeyi Dem(x,z) ile gösterelim. Burada
ile
arasında aritmetik bir bağıntı olacaktır. Bu bağıntı, tıpkı bir formüller dizisinin Gödel sayısını anlatırken verdiğimiz örnekte,
ile
sayıları arasındaki bağıntıya benzer.
ile
arasındaki bu bağıntıyı, dem(x,z) ile gösterelim. (Burada dem, demonstration=kanıtlama,ispat’ kelimesinin kısaltmasıdır.)
- sub(m,17,m) : Yukarıda,
“y’nin en az bir ardılı vardır.” formülünün Gödel sayısını m ile göstermiştik. Bu formülde, Gödel sayısı 17 olan y değişkeninin yerine m koyarak
formülünü elde edebiliriz. Diğer taraftan,
biçiminde yazılabildiğinden, yeni formülümüz;
şeklinde olacaktır. İşte, Gödel sayısı m olan bir formülde, Gödel sayısını 17 olan değişkenin yerine, m koymakla elde edilen yeni formülün Gödel sayısını sub(m,17,m) ile gösterelim. Bu ifadenin üst matematiksel ifadesi içinse Sub(m,17,m) gösterimini kullanalım.
Şimdi artık Gödel’in yaptığı ispattan bahsedebiliriz. İspatı 5 temel adımda ele alalım:
(1) İlk amacımız, “G, PM’nin kuralları kullanılarak kanıtlanamaz” ifadesini sağlayacak bir G formülü elde etmektir. Bunun için önce Dem(x,z) formülünü ele alalım. Dikkat edersek bu formül bize, Gödel sayısı
olan bir formülün kanıtlanabilir olduğunu söylüyor. Dolayısıyla
Dem(x,z), Gödel sayısı
olan bir formülün kanıtlanamaz olduğu anlamına geliyor.
Şimdi de Dem(x, Sub(y,17,y)), yani “Gödel sayısı sub(y,17,y) olan bir formül kanıtlamaz” anlamına gelen formülü ele alalım ve bunun Gödel sayısını n ile gösterelim. Burada, y yerine n koyarak, ulaşmak istediğimiz G formülünü elde edelim. Yani G,
Dem(x, Sub(n,17,n)) olsun.
G’yi elde ederken, Gödel sayısı n olan bir formülde, Gödel sayısı 17 olan terimin (yani y’nin) yerine n koyduk. Dolayısıyla, G’nin Gödel sayısı sub(n,17,n) olacaktır. Diğer taraftan G bize, Gödel sayısı sub(n,17,n) olan formülün kanıtlanamayacağını söylüyor. Demek ki G, “G kanıtlanamaz” ifadesinden başka bir şey değil.
(2) Sıradaki amacımız, “G kanıtlanabilir
kanıtlanabilir” çift gerektirmesini ispatlamak olacak. Eğer G’nin kanıtlanabilir olsaydı,
(yani, “G, PM içinde kanıtlanabilirdir” formülü) de kanıtlanabilirdi. Gerektirmenin diğer yönünü de benzer bir akıl yürütme ile göstermek mümkündür.
Bir önceki yazıdan, tutarlı sistemler içinde, birbiriyle çelişen teorem çiftlerinin elde edilemeyeceğini hatırlayalım. Bu demek oluyor ki, tutarlı bir sistem içerisinde G’yi kanıtlamak mümkün değildir.
(3) G, doğru bir ifade, yani PM’nin bir teoremidir. Bunun sebebi, G’nin, (2)’de elde ettiğimiz sonuçla paralel olması, yani kendisinin PM içerisinde kanıtlanabilir olmadığını ifade etmesidir.
(4) G, onu oluşturmak için kullanılan aksiyomatik sistem içinde, doğru olduğunu halde kanıtlanamayan bir ifadedir. Demek ki PM tam değil, eksiklidir. Gödel ayrıca, bu sisteme, G’nin kanıtlanabilmesine yardım edecek aksiyomlar eklense bile, doğru fakat kanıtlamaz olan bir formülü oluşturmanın mümkün olduğunu, ve hatta bu sürecin sonsuza kadar devam ettirilebileceğini de göstermiştir.
(5) Bu son adımda, “PM tutarlıdır” varsayımı yapalım ve buradan çıkacak sonuçları inceleyelim. Bir önceki yazıdan,tutarlı bir aksiyomatik sistemde, aksiyomlardan türetilemeyecek, yani kanıtlanamayacak en az bir formül olması gerektiğini biliyoruz. Bu durumu, Dem(x,y), yani, “Gödel sayısı x olan hiçbir formül dizisi ile kanıtlanamayacak olan, y Gödel sayılı bir formül vardır” biçiminde ifade edebiliriz. Bu ifadeyi A ile gösterelim.
Diğer taraftan, “PM tam değildir” formülü bize bir yerlerden tanıdık geliyor mu, bir bakalım. “PM tam değildir”, önermesi PM içinde, doğru olan fakat kanıtlanamayan bir X formülü vardır anlamına gelir. Biraz önce tam da bu tarife uyan bir G formülü elde etmiştik. İşte bu sayede, “PM tam değildir” formülünü, “G, PM’de kanıtlanamaz” formunda ifade edebiliriz. Bu ifade ise aslında G’nin kendisidir.
Sonuç olarak; “PM tutarlıdır” formülü A, “PM tam değildir” formülü ise G ile gösterilebildiğinden, “PM tutarlı ise tam değildir” önermesi “” şeklinde ifade edilebilir. Her ne kadar burada göstermeyecek olsak da,
‘nin PM içinde kanıtlanabilir olduğu biliniyor.
Şimdi A formülünün PM içinde kanıtlanabilir olmadığını gösterelim. Tersine A, PM’de kanıtlanabilir olsun. Bu durumda, “ de kanıtlanabilir olduğundan, G de kanıtlanabilir olacaktır ve bu bir çelişkidir. Demek ki, PM’nin tutarlılığını PM içerisinde kanıtlamak mümkün değildir. Herhangi bir S sisteminin tutarlılığını kanıtlamak için daha güçlü bir T sistemine ihtiyaç vardır. Örneğin, Peano aksiyomlarının tutarlılığı küme teorisi kullanılarak gösterilebilir, ancak doğal sayılar teorisi kullanılarak gösterilemez.
Ve perde…
Gödel’in I. Eksiklik Teoremi: Temel aritmetiksel doğruları kanıtlayabilen herhangi bir tutarlı biçimsel sistem için, doğru olan ancak sistem içinde kanıtlanamayan bir aritmetiksel ifade oluşturmak mümkündür.
Gödel’in II. Eksiklik Teoremi: Temel aritmetiksel doğruları kanıtlayabilen herhangi bir tutarlı biçimsel sistem için, o sistemin tutarlılığına (kendi içinde) karar verebilmek için gerek ve yeter koşul sistemin tutarsız olmasıdır. (Yani aslında, “bu sistem tutarlıdır” sonucuna sistemin kendi olanaklarını kullanarak ulaşmak mümkün değildir.)
Gödel’in eksiklik teoremi, insan zihninin sınırlarına dair birçok felsefik tartışmaya sebep olmuştur. Ama bence en güzel yankısı, Cambridge üniversitesinde yüksek lisans öğrencisiyken bu teoremle tanışan Alan Turing’in zihninde olandır.
17. yüzyılda Alman matematikçi Leibniz, herhangi bir matematiksel ifadeyi girdi olarak okuyabilen ve matematiğin aksiyomlarına dayanarak doğru ya da yanlış olduğunu belirleyebilen bir makine fikrini öne sürmüştür. Turing, Leibniz’in açtığı yoldan yürüyerek, herhangi bir girdiyi işleyebilen ve bir sonucu hesaplayabilen makinelerin matematiksel tasarımını formüle etmeye çalışmıştır. En basit haliyle bir Turing makinesi, modern bir bilgisayar programına benzetilebilir.
Turing, günümüzde Durma Problemi (Halting Problem) olarak bilinen ve aşağıdaki gibi ifade edilebilecek olan bir problem üzerinde çalışmıştır:
“Başka bir programın durup durmayacağına karar verecek, (yani, program yürütmeyi bitirecek mi yoksa sonsuz bir döngüye mi girecek sorusuna cevap verebilecek) bir program olabilir mi?”
Turing, böyle bir programın var olamayacağını, Gödel’in çalışmasına benzer bir şekilde çelişkiye varma yöntemi kullanarak ispatlamıştır. Gödel matematiğin, Turing ise Bilgisayar Biliminin bir anlamda ‘eksik’ olduğunu kanıtlamış ve bu iki deha aslında bilmenin önündeki teorik sınırları ortaya koymuşlardır. Bunlara ek olarak, teoride çözebileceğimiz, ancak çözümü hesaplamak çok uzun sürdüğü için pratikte çözemeyeceğimiz başka problemler de vardır. İşte tam bu noktada konu, “P ve NP problemlerine” ve 1 milyon dolarlık “P=NP midir?” sorusuna gelir. Bu problemler nelerdir, “P=NP midir?” sorusuna bir yanıt bulunursa dünya nasıl değişir gibi konulara başka bir yazıda değinmek daha doğru olacaktır.
Kapanışı Gödel’in güzel bir sözüyle yapalım:
“Ya matematik insan zihni için fazla büyüktür ya da insan zihni bir makineden daha fazlasıdır.“
KAYNAKLAR
1) Ernest Nagel, James R. Newman, Gödel’s Proof, New York University Press, 1958.
2) Sebastian Bader, Godel’s Incompleteness Theorems, Knowledge Representation and Reasoning Seminar, April 25th, 2006.
3) Ernest Nagel, James R. Newman, Gödel Kanıtlaması, çev. Bülent Gözkan, Boğaziçi Üniversitesi Yayınevi, 2007.
4) https://3010tangents.wordpress.com/2014/11/26/turing-leibniz-and-hilberts-entscheidungsproblem/