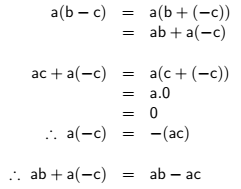Neden Matematikçi Olunur? Evrenin Kaynak Koduna Yolculuk

Posted on 9 Ağustos 2025 by esrakorkmaz

Evren bir kitap ise, hangi dilde yazılmıştır? Güzellik, yalnızca bir sanat eserinde veya bir günbatımında mı bulunur; yoksa kusursuz bir ispatın sadeliğinde de saklı olabilir mi? İnsan zihni, kendi sınırlarını zorlayıp, hiç görmediği boyutları ve hiç hayal etmediği yapıları keşfedebilir mi? Bu soruların kesişim kümesinde, insanlığın en kadim, en güçlü ve belki de en yanlış anlaşılan arayışı yatar: Matematik.

Matematik denilince zihinlerde genellikle çözülmesi imkansız formüller canlanır. Bu imaj, matematiğin asıl doğasını, onun dinamik ve yaratıcı ruhunu gizleyen bir perdedir. Matematikçi olmak, sayılarla boğuşan bir teknisyen olmak değil; desenlerin, yapıların ve olasılıkların şairi olmaktır. Bu, görünenin ardındaki görünmeyeni anlama, kaosun içindeki düzeni bulma ve saf düşünce gücüyle yeni dünyalar inşa etme sanatıdır.

Tarihin Akışını Değiştiren Aykırı Zihinler: Matematikçiler

Matematik tarihi, imkansız denilenin peşine düşen ve medeniyetin rotasını sadece düşünce gücüyle değiştiren dâhilerin ve vizyonerlerin destanıdır.

Milattan binlerce yıl önce Babilliler, bugün hala zamanı ölçmek için kullandığımız 60’lık sayı sistemini geliştirerek gökyüzünü haritaladılar. Onlar için matematik, göklerin düzenini yeryüzüne indirme aracıydı. Sonra Öklid sahneye çıktı. Elementler adlı eseriyle, sadece birkaç basit aksiyomdan yola çıkarak devasa bir mantık imparatorluğu kurdu. İki bin yıldan fazla bir süre boyunca insanlığa sadece geometriyi değil, tutarlı ve kanıta dayalı düşünmenin ne demek olduğunu öğreten bir anayasaydı bu.

Orta Çağ’da, Avrupa karanlığa gömülmüşken, Bağdat’taki Bilgelik Evi’nde (Beyt’ül Hikme) bir yıldız parladı: Harezmî. Onun “El-Cebr” çalışması, sadece bugünkü cebir kelimesinin kökeni olmakla kalmadı, aynı zamanda bilinmeyenleri çözmek için izlenen sistematik, adım adım ilerleyen yöntemi, yani algoritmayı dünyaya armağan etti. Bugün hayatımızı yöneten her bir yazılım, Harezmî’nin o gün attığı temelin üzerinde çalışıyor.

Ve sonra sahneye Newton ve Leibniz çıktı. Birbirlerinden habersiz, değişimin matematiğini, yani Kalkülüs’ü icat ettiler. O ana kadar statik ve durağan nesneleri ölçebilen matematik, artık hareket eden, büyüyen, değişen her şeyi anlayabiliyordu. Gezegenlerin yörüngesinden bir merminin yoluna, bir salgının yayılım hızından ekonomideki dalgalanmalara kadar, modern bilimin tamamı bu dille yazıldı. Onlar, evrenin fiillerini ve zarflarını anlayan ilk insanlardı.

19. yüzyılda Gauss, Bolyai ve Lobaçevski gibi matematikçiler, Öklid’in iki bin yıllık imparatorluğuna meydan okudular. “Ya paralel doğrular bir yerde kesişiyorsa?” gibi delice görünen bir soru sordular. Bu soyut geometriler, on yıllar boyunca sadece matematikçilerin zihin jimnastiği olarak kaldı. Ta ki Einstein evrenin dokusunu açıklamak için bu gerçek dışı geometriye ihtiyacı olduğunu fark edene kadar. Saf, soyut düşünce, bir kez daha realitenin en derin sırrının anahtarı olmuştu.

Ve son olarak Alan Turing. İkinci Dünya Savaşı’nda Nazilerin kırılamaz denen Enigma şifresini, soyut mantık ve sayılar teorisinin gücüyle kırarak milyonlarca hayat kurtardı. Ama daha da önemlisi, bunu yaparken tasarladığı teorik evrensel makine, bugünkü dijital çağın ve bilgisayarların doğum belgesi oldu. Bir matematikçi, saf düşünce gücüyle hem bir savaşı bitirdi hem de yepyeni bir teknoloji çağı başlattı.

Düşüncenin Gücüyle Dünyayı Şekillendirmek

Matematiksel düşünce yapısı, yani karmaşık sistemlerdeki desenleri, yapıları ve ilişkileri görme yeteneği, çağımızın en değerli zihinsel aracıdır. Bu araçla donanmış bir zihin, teknolojinin, finansın ve bilimin kesişimindeki en heyecan verici alanların doğal bir oyun kurucusudur.

Bu gücün en somut çıktılarından biri, her gün içinde yaşadığımız dijital evrenin temelindeki görünmez mimaridir. Banka hesabımızı koruyan şifreleme, büyük sayılarla yapılan bazı matematiksel işlemlerin kolay, ters işlemlerinin ise günümüz teknolojisiyle neredeyse imkânsız olması gerçeğine dayanır. Bu hesaplama zorluğu bir zafiyet olarak değil, bir kaynak olarak görülmüş ve üzerine dijital güvenliğin sarsılmaz kalesi inşa edilmiştir. Bu görünmez kalelerin duvarları sayılar teorisiyle örülürken, içinde yaşadığımız dijital dünyanın şehir planlaması ve lojistiği ise bambaşka bir matematiksel dala, çizge teorisine aittir. İnternetin kendisi, düğümler ve bağlantılardan oluşan dev bir çizgedir. En kısa teslimat rotasını bulan bir kargo şirketi veya bir salgının yayılım ağını analiz eden bir epidemiyolog, bu teorinin prensiplerini kullanarak kaosu optimize eder ve sistemlerin daha akıllı, daha hızlı ve daha verimli çalışmasını sağlar.

Ancak dünya her zaman bu kadar düzenli ve öngörülebilir ağlardan oluşmaz. Bu yapıların ötesinde, içinde rastlantının ve olasılığın dans ettiği daha kaotik sistemler vardır. Finansal piyasalar bunun en belirgin örneğidir. Klasik kalkülüs gezegenlerin yörüngelerini hesaplarken, stokastik kalkülüs rastlantısallığın matematiğini yazar. Quant olarak bilinen nicel analistler, bu ileri aracı kullanarak riskin fiyatını belirler. Bir hisse senedi opsiyonunun bugünkü adil değerini, gelecekteki binlerce olası senaryoyu modelleyerek hesaplarlar. Onlar falcı değillerdir; belirsizliğin yapısını anlar, riskin olasılığını ölçer ve bu bilgiyi milyarlarca dolarlık kararlara dönüştürürler. Bu, rastlantıyı evcilleştirme sanatıdır.

Rastlantının içindeki bu desen arayışı, matematiğin en modern ve devrimci uygulama alanlarından birinin kapısını aralar: Yapay Zeka. Eğer finans piyasaları gürültülü bir veri okyanusuysa, yapay zekanın uğraştığı dünya, içinde resimlerin, seslerin ve metinlerin olduğu devasa bir veri evrenidir. Bir makinenin bir fotoğraftaki nesneyi tanıması bu evrende bir anlam çıkarma eylemidir. İşte lineer cebir, bir resmin milyonlarca piksellik veri kaosunu, bilgisayarın tanıyabileceği anlamlı bir yapıya dönüştürüp, veriyi temel özelliklerini ortaya çıkaracak şekilde yeniden boyutlandırır. Ardından optimizasyon, bir heykeltıraşın mermeri yontması gibi, sistemin milyonlarca parametresini yavaş yavaş yontarak doğru tahminler yapmasını sağlar. Matematikçi bu alanda makinenin öğrenme denilen sürecinin ta kendisini tasarlar.

Matematikçinin zihni, sadece dijital bitlerin veya veri noktalarının soyut dünyasında değil, aynı zamanda dokunabildiğimiz fiziksel gerçekliğin temel yasalarında da gezinir. Örneğin lineer cebir, aynı zamanda bir köprünün taşıyacağı yükü hesaplayan mühendisin de temel aracıdır. Ancak fiziksel dünyanın asıl dili, değişimin kendisidir ve bu dilin gramerine diferansiyel denklemler denir. Bu denklemler, bir sistemin şimdiki durumuna bakarak bir sonraki anda ne yapacağını anlatan matematiksel cümlelerdir. Bir mühendis, yeni bir aracın çarpışma anındaki davranışını daha tek bir vida bile sıkılmadan simüle edebilir. Bir iklim bilimci, atmosferdeki değişimlerin gelecekteki sıcaklıkları nasıl etkileyeceğini bu denklemlerle modeller. Matematikçiler bu denklemleri çözerek, adeta fiziksel gerçekliğin geleceğini okur ve daha iyi bir gelecek tasarlamamız için bize senaryoyu sunarlar.

Sonuç olarak, gelecekte matematikçilere olan ihtiyaç artarak devam edecektir. Çünkü dünya daha karmaşık, daha veri odaklı ve daha fazla optimize edilmiş sistemlere bağımlı hale geldikçe, bu sistemlerin temelindeki mantığı kuracak, yapıları tasarlayacak ve en zorlu problemleri çözecek olanlar, yine o temel dilin ustaları olacaktır. Tercih listenizdeki o “Matematik Bölümü” satırı, sadece akademik bir programdan ibaret değildir. O, bir düşünce biçimine, bir dünya görüşüne ve geleceği şekillendirecek en temel araç setine açılan bir davetiyedir. Evrenin kaynak koduna erişim izni talep etmektir. Dünya, cevapları bilen insanlarla dolu. Ancak ilerlemeyi sağlayanlar, doğru soruları sorabilenlerdir. Matematik, size o soruları sorma cesaretini ve cevapları inşa etme gücünü verecektir.

Görünmeyen Boyutlar: Matematikte Uzay Kavramının Evrimi

Posted on 28 Mart 2025 by esrakorkmaz

Cevapla

Matematiğin temel taşlarından biri, belki de en önemlisi olan “uzay” kavramı, ilk bakışta basit görünse de derin anlamlar taşır. Bu kavram, matematiğin farklı dallarını birbirine bağlayan bir köprü görevi görür ve dünyayı anlama çabamıza rehberlik eder.

Uzay, en genel anlamıyla, nesnelerin ve olayların içinde bulunduğu, konumlarının ve hareketlerinin tanımlanabildiği bir ortamdır. Sadece nesnelerin nerede olduğunu değil, aynı zamanda nesneler arasındaki ilişkileri de tanımlamamızı sağlar. Bir matematikçinin gözüyle ise uzay, üzerinde istediğimiz gibi çalışabileceğimiz, kurallarını bizim belirlediğimiz bir oyun alanıdır.

Uzay kavramının kökenleri, insanlığın çevresini gözlemleme ve deneyimleme çabalarına dayanır. İlk insanlar hayatta kalabilmek için mekânsal ilişkileri anlamak zorundaydılar. “En yakın su kaynağı ne kadar uzakta ve hangi yönde?”, “Bu iki av sahası arasındaki mesafe yürüyerek kaç gün sürer?”, “Balık tutmak için gölün en derin yeri neresi olabilir?” gibi sorular, insanlığın ilk uzamsal problemlerinden bazılarıdır.

Antik Mısır ve Mezopotamya medeniyetleri, uzay kavramını pratik ihtiyaçlar doğrultusunda geliştirmişlerdir. Özellikle Mısır’da, Nil Nehri’nin yıllık taşkınları arazi sınırlarını belirsizleştirdiğinden, bu sınırların güvenilir bir şekilde yeniden çizilmesi zorunluluğu doğmuştur. İşte bu pratik zorunluluk, Yunanca geo (yer) ve metria (ölçüm) kelimelerinden türeyen ve tam olarak “yer ölçümü” anlamına gelen geometrinin gelişmesinde kilit bir rol oynamıştır.

Uzay kavramının ilk soyut ve sistematik ifadesi, M.Ö. 300 civarında İskenderiyeli Öklid tarafından “Elementler” adlı ölümsüz eserinde sunulmuştur. Öklid, geometriyi aksiyomatik bir sistem üzerine inşa ederek, uzayın temel özelliklerini tanımlamıştır ve o zamana kadar kimsenin tam olarak başaramadığını yaparak, dağınık ve sezgisel geometrik bilgileri sağlam bir mantıksal çerçeveye oturtmuştur. Şimdi Öklid’in meşhur beş aksiyomunu hatırlayalım:

İki farklı noktadan yalnız bir doğru geçer.
Bir doğru parçası, her iki yönde de sürekli (sonsuza dek) uzatılabilir.
Bir merkez ve bir yarıçap (mesafe) verildiğinde, bir çember çizilebilir.
Bütün dik açılar birbirine eşittir. (90 derece, dünyanın neresine giderseniz gidin 90 derecedir.)
Bir doğru, başka iki doğruyu kestiğinde, aynı tarafta oluşan iç açıların toplamı iki dik açıdan küçükse, bu iki doğru o tarafta uzatılmaya devam edildiğinde mutlaka kesişir. (“Paralel doğrular kesişmez” olarak da bilinen o meşhur beşinci aksiyom. Tarih boyunca matematikçileri en çok uğraştıran, “Acaba bu gerçekten bir postulat mı, yoksa diğerlerinden çıkarılabilir mi?” diye düşündüren madde.)

Beşinci aksiyom, diğerlerinden daha karmaşık olması ve doğrudan sezgisel olmaması nedeniyle yüzyıllar boyunca tartışılmıştır. Onu ilk dört aksiyomdan mantıksal olarak türetme yönündeki sayısız girişim sonuçsuz kalınca, 19. yüzyılın başlarında radikal bir fikir ortaya çıkmıştır: Ya bu aksiyom değiştirilebilir veya yerine başka bir alternatif konulabilirse? İşte bu sorgulama, mantıksal olarak kendi içinde tutarlı, ancak sonuçları Öklid geometrisinden farklı olan yepyeni geometrilerin keşfine yol açmıştır. Gauss, Bolyai ve Lobachevsky, birbirlerinden bağımsız olarak, bugün hiperbolik geometri olarak bilinen yapıyı ortaya koymuşlardır. Riemann ise, genel bir eğrilik kavramı çerçevesinde eliptik geometriyi tanımlamıştır. Öklid dışı geometrilerin keşfiyle, fiziksel uzayın mutlak bir geometrisi olduğu fikri sorgulanır hale gelmiştir. Bunun yerine uzay, belirli aksiyomlar tarafından tanımlanan matematiksel bir yapı olarak görülmeye başlanmıştır.

Rönesans döneminde sanat ve bilim arasındaki güçlü etkileşim, uzay kavramının anlaşılmasında yeni ufuklar açmıştır. Özellikle 15. yüzyılda İtalyan sanatçılar ve mimarlar, başta Filippo Brunelleschi ve Leon Battista Alberti olmak üzere, perspektif kurallarını geliştirip sistematikleştirerek üç boyutlu dünyayı iki boyutlu yüzeylere başarılı bir şekilde aktarmayı başarmışlardır. Perspektif, nesnelerin gözlemcinin konumuna göre nasıl göründüğünü betimleyen ve bu görünümü matematiksel ilkelere dayandıran bir temsil tekniğidir.

17. yüzyılda Desargues ve Pascal gibi matematikçiler, perspektif çiziminin altında yatan geometrik prensipleri ve dönüşümleri inceleyerek projektif geometrinin temellerini atmışlardır. Projektif geometri, Öklid geometrisindeki paralel doğruların sonsuzdaki bir noktada kesiştiği fikrini temel alır. Bu yaklaşım, Öklid düzlemine sonsuzdaki noktaları (ve sonsuzdaki doğruyu) ekleyerek onu genişletir; sonuç olarak projektif düzlemde paralel doğrular kalmaz, her iki doğru mutlaka bir noktada kesişir. Bu yapı, Öklid geometrisinin zarif bir genelleştirmesi olarak görülebilir ve perspektif çizimlerinin altında yatan değişmezliklerin (örneğin, noktaların bir doğru üzerinde kalması gibi) matematiksel analizini mümkün kılar.

Daha sonraki dönemlerde Poncelet ve von Staudt gibi matematikçiler, projektif geometriyi daha da ileri taşımışlardır. Özellikle von Staudt’un katkısı önemlidir; çünkü projektif geometriyi tamamen koordinatlardan ve mesafe (metrik) kavramından bağımsız olarak, yalnızca noktalar, doğrular ve bunların kesişme ilişkileri üzerine kurulu aksiyomatik bir sistem olarak formüle etmiştir. Bu yaklaşım, uzayın temel yapısını, ölçüm kavramlarından arındırarak anlama yönündeki önemli ve erken bir adımı temsil etmektedir.

Uzay kavramının gelişiminde büyük adımlardan bir diğeri de 17. yüzyılda atılmıştır. Descartes, “La Géométrie” adlı eserinde, düzlemdeki noktaları iki sayıdan oluşan sıralı ikililerle (x, y) temsil ederek, geometri ile cebiri birleştirmiştir. Bilim tarihi, o parlak ‘Evreka!’ anlarının dramatize edilmiş hikayelerine bayılır: Newton ve elma, Arşimet ve hamam tası…Rivayete göre, Descartes koordinat sistemini bir sabah yatakta bir sineğin hareketini takip ederken keşfetmiştir. Sineğin konumunu tanımlamak için iki duvara olan mesafesini kullanması gerektiğini fark etmiştir.

Devrim niteliğinde bir yenilik olan koordinat sisteminin kullanımı, geometrik nesneleri cebirsel denklemlerle ifade etmeyi mümkün kılmıştır. Örneğin, düzlemde bir doğru, $ax + by + c = 0$ şeklinde birinci dereceden bir denklemle; bir çember ise $(x - h)^2 + (y - k)^2 = r^2$ şeklinde bir denklemle temsil edilmiştir. Descartes’ın analitik geometrisi, uzay kavramına yeni bir bakış açısı getirmiştir. Artık uzay, sadece şekillerin ve cisimlerin içinde bulunduğu bir ortam değil, aynı zamanda sayılarla temsil edilebilen ve cebirsel işlemlerle manipüle edilebilen bir yapı olarak görülmeye başlanmıştır. Bu yaklaşım, diferansiyel ve integral hesabın gelişimini de kolaylaştırmış ve modern matematik için yeni kapılar açmıştır. Descartes’ın koordinat sistemi, n-boyutlu uzayların tanımlanmasına da olanak sağlamıştır. Düzlemdeki (2-boyutlu) ve uzaydaki (3-boyutlu) noktaların koordinatlarla temsil edilmesi fikri, sıralı n-lilerle temsil edilen n-boyutlu uzaylara genelleştirilmiştir. Bu genelleştirme, 19. yüzyılda vektör uzayları ve Riemann geometrisi gibi kavramların gelişimine zemin hazırlamıştır.

19. yüzyılın ortalarına doğru, matematikçilerin uzay kavramına yaklaşımı giderek daha soyut ve genel bir nitelik kazanmıştır. Bu dönemde Grassmann‘ın öncü çalışmaları ve daha sonra Peano‘nun katkılarıyla vektör uzaylarının aksiyomatik tanımı geliştirilmiştir. En temel haliyle bir vektör uzayı, vektör olarak adlandırılan elemanlardan oluşan ve üzerinde iki temel işlem (vektör toplaması ve skalerle çarpma) tanımlanmış bir kümedir. Bu işlemlerin, toplamanın birleşme ve değişme özelliği, skalerle çarpmanın vektör toplamı üzerine dağılma özelliği gibi belirli kuralları sağlaması gerekir.

Günlük hayatta veya temel fizikte vektörleri genellikle yönü ve büyüklüğü olan oklar (örneğin hız, kuvvet, yer değiştirme) olarak görselleştirsek de, matematiksel vektör uzayı kavramı çok daha genel ve soyuttur. Bu güçlü soyutlama sayesinde, polinomlar veya fonksiyonlar gibi ilk bakışta geometrik oklarla ilgisi olmayan nesneler bile belirli koşullar altında vektör olarak ele alınabilir. Örneğin, belirli bir aralıkta tanımlı tüm sürekli fonksiyonların kümesi, fonksiyonların toplanması ve bir sabitle çarpılması işlemleri altında bir vektör uzayı oluşturur. Bu, fonksiyonel analizin temelini oluşturan önemli bir fikirdir.

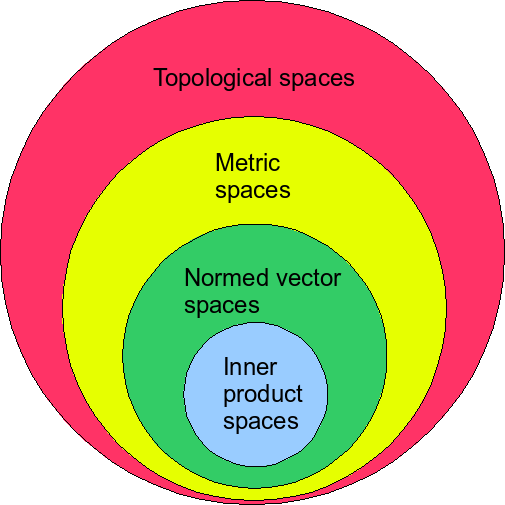
Vektör uzayı, uzayın cebirsel yapısını tanımlar. Ancak, uzayın geometrik özelliklerini (uzunluk, açı, diklik vb.) tanımlamak için, vektör uzayına bir yapı eklemek gerekir: İç çarpım. İç çarpım uzayı, vektör uzayına geometrik bir anlam katar. Örneğin, iki vektörün iç çarpımı sıfır ise bunların birbirine dik olduğunu söyleyebiliriz. Ayrıca, Öklid uzayında kullanılan “Pisagor teoremi” ve “kosinüs teoremi” gibi temel geometrik ilişkiler, iç çarpım uzaylarına genelleştirilebilir.

19. yüzyılın sonu ve 20. yüzyılın başında, matematikçiler uzayları “mesafe” kavramı üzerine inşa etmeyi düşünmüşlerdir. Fréchet, 1906 yılında metrik uzay kavramını tanıtmıştır. Metrik uzay, üzerinde bir mesafe fonksiyonu (metrik) tanımlanmış bir kümedir. Bu fonksiyon, uzayın herhangi iki noktası arasındaki uzaklığı belirler ve belirli aksiyomları sağlar (örneğin, üçgen eşitsizliği). Burada işin güzel tarafı, mesafe kavramının fiziksel uzaklıkla sınırlı olmamasıdır. Örneğin, iki kelimenin birbirine ne kadar benzediğini ölçen “Levenshtein mesafesi” ya da iki DNA dizisinin birbirinden ne kadar farklı olduğunu ölçen “Hamming mesafesi” gibi metrikler de tanımlanmıştır.

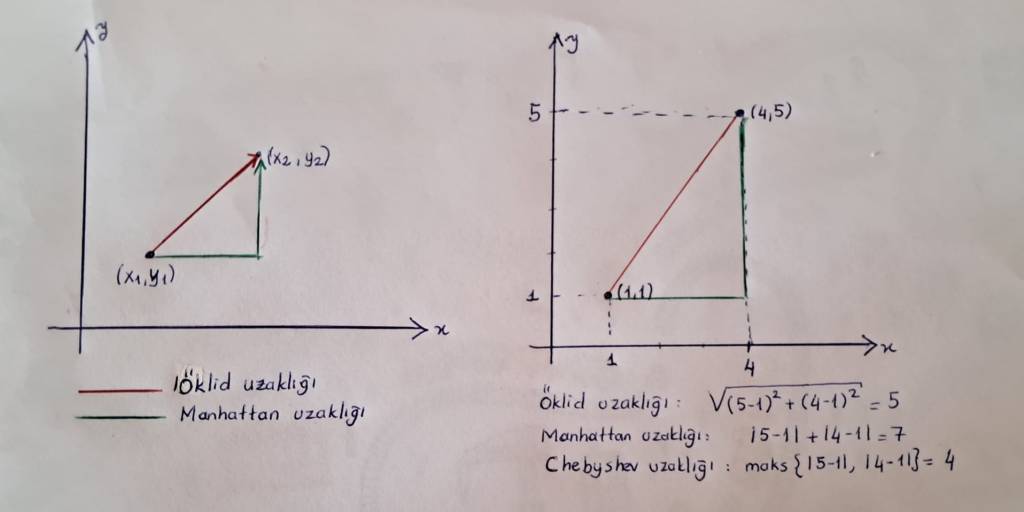
Bu soyut mesafe ölçme yeteneği, veri bilimi ve makine öğrenmesi gibi modern alanlar için de temel bir araç haline gelmiştir. Bu alanlarda amaç genellikle, verilerin temsil edildiği özellik uzaylarındaki (feature spaces) noktalar arasındaki benzerliği veya farklılığı nicel olarak ölçmektir. Sınıflandırma veya kümeleme gibi pek çok algoritmik görev, bu uzaylarda tanımlanan Öklid mesafesi (düz çizgi uzaklığı) veya Manhattan mesafesi (şehir blokları gibi dik açılı hareket) gibi çeşitli metrikleri kullanarak noktaların birbirine ne kadar yakın ya da uzak olduğunu hesaplamaya dayanır. Dolayısıyla metrik uzay yapısı, veriler arasındaki ilişkileri anlamak ve buna dayalı algoritmik kararlar vermek için gereken matematiksel çerçeveyi de sunmaktadır.

Metrik uzaylarda, uzay yapısı mesafe kavramı üzerine kurulmuştur. Ancak matematikçiler, bazı durumlarda bu mesafe odaklı yaklaşımın gereğinden fazla kısıtlayıcı olabileceğini fark etmişlerdir. Süreklilik, bir noktaya istenildiği kadar yakın olabilme veya bir şeklin bağlantılı olup olmaması gibi bazı temel özelliklerin, noktalar arasındaki kesin sayısal uzaklıktan ziyade, daha temel bir komşuluk veya yakınlık ilişkisiyle ilgili olduğu görülmüştür.

Bir haritadaki şehirleri düşündüğümüzde bu fikir netleşebilir: Ankara’nın Eskişehir’e komşu olduğunu bilmek, bu iki şehir arasında kaç kilometre olduğunu bilmekten daha temel bir bağlantı bilgisi sunabilir. Ya da bir bölgenin (örneğin Türkiye ana karasının) bağlantılı olup olmadığını anlamak için, içindeki herhangi iki nokta (şehir) arasında kesintisiz bir yolun var olup olmadığına bakılabilir. Bu yolun ne kadar uzun olduğu (mesafe) değil, böyle bir yolun bulunması önemlidir. İşte bu daha genel yakınlık ve bağlantı yapısını matematiksel olarak tanımlamak için 20. yüzyılın başlarında Topolojik Uzay kavramı geliştirilmiştir.

Topolojik uzay, bir küme ve bu küme üzerinde tanımlanmış, adına açık kümeler denen özel bir alt küme ailesinden oluşur. Bu açık kümeler ailesi, belirli birleşim ve kesişim kurallarını sağlamak zorundadır ve bir noktanın hangi diğer noktalarla komşu veya yakın kabul edileceğini belirleyen temel yapıyı oluşturur. Bu yaklaşımın gücü şuradadır: Artık uzay sürekli bir şekilde eğilip bükülebilir (tıpkı meşhur örnekteki, hamurdan yapılmış bir kahve fincanının bir simide/donuta dönüştürülmesi gibi). Bu tür deformasyonlar sırasında mesafeler, açılar gibi metrik özellikler değişse de, topolojinin ilgilendiği temel yapısal özellikler (örneğin, bir şeklin tek parça kalması veya içindeki delik sayısı) değişmez. Topoloji, işte bu sürekli deformasyonlar altındaki değişmezlerin matematiği olarak görülebilir; şekillerin en esnek ve temel özelliklerini inceler.

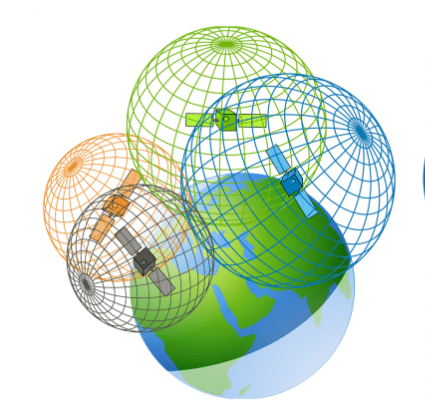
Topolojik uzaylar müthiş bir genellik sunmuştur fakat matematikçiler ve fizikçiler, bu genelliği de kaybetmeden, bildiğimiz Öklid geometrisinin özelliklerini yerel olarak taşıyan daha kullanışlı yapılara ihtiyaç duymuşlardır. İşte bu noktada Manifoldlar sahneye çıkmıştır. Bir manifold, en temel tanımıyla, yerel olarak (yani küçük bir komşulukta) bildiğimiz Öklid uzayına benzeyen bir topolojik uzaydır. Uzayın her noktasına yeterince yakından baktığımızda, gördüğümüz manzara düz bir kağıt parçası gibi olmalıdır. Tıpkı üzerinde yaşadığımız Dünya gibi. Hepimiz biliyoruz ki dünyanın küresel bir yapısı olmasına rağmen, küçük bir alanda bize dümdüz görünür. İşte manifoldlar, bu yakın planda düz, genel planda eğri ikiliğini matematikselleştiren yapılardır. Bu fikir o kadar etkili olmuştur ki, Einstein’ın Genel Görelilik Teorisi, evrenimizin dokusunu, yani uzay-zamanı, kütle ve enerjinin etrafında bükülen dört boyutlu bir manifold olarak tasvir etmiştir.

Manifoldlar evrenin büyük resmini çizerken, 20. yüzyıl başlarında fizikçiler atomun içine daldıklarında karşılaştıkları kuantum gariplikleri için yepyeni bir sahneye ihtiyaç duymuşlardır. Çünkü, parçacıkların aynı anda birden fazla yerde olabilmesi gibi klasik mantığa sığmayan durumları açıklamak için, sonsuz olasılığı barındırabilen sonsuz boyutlu uzaylar gerekmektedir. Bu noktada fizikçilerin imdadına yetişen yapı Hilbert uzayları olmuştur. Bu uzaylar, üzerinde uzunluk/açı ölçmemizi sağlayan bir iç çarpım bulunan, birbirine giderek yaklaşan her vektör dizisinin mutlaka yine uzayın içindeki bir noktaya yakınsadığını garantileyen (yani, tam) ve en önemlisi genellikle sonsuz boyutlu olan vektör uzaylarıdır. Bir kuantum sisteminin tüm olası durumları, bu soyut uzaydaki bir vektörle (dalga fonksiyonu) ifade edilmiştir. Kuantumun o meşhur süperpozisyon, belirsizlik gibi ilkeleri, Hilbert uzayının matematiksel yapısı sayesinde kesin bir zemine oturmuştur.

Hilbert uzayları, iç çarpımın sağladığı zengin geometrik yapıyla öne çıkarken, matematikçiler daha da genel bir soru sormuşlardır: “Ya vektörlerin sadece büyüklüğünü (normunu) biliyor fakat aralarındaki açıyla ilgilenmiyorsak?” İşte bu noktada, Banach uzayları matematik dünyasına girmiştir. Banach uzayları, tam (yani yine limitlere kapalı) ve üzerinde bir uzunluk ölçüsü tanımlanmış, ancak iç çarpım zorunluluğu olmayan vektör uzaylarıdır. Hilbert uzayları, Banach uzaylarının özel bir alt sınıfı olarak görülebilir.

Matematikteki bu soyutlama ve genelleştirme yönelimi, 20. yüzyılın ortalarında Kategori Teorisi ile zirveye ulaşmıştır. Eilenberg ve Mac Lane tarafından geliştirilen bu yaklaşım, matematikçileri tek tek nesnelerin (örneğin farklı türdeki uzayların) iç yapısından ziyade, bu nesneler arasındaki ilişkilere yöneltmiştir. Kategori teorisi, farklı uzay türlerini (topolojik, vektör, Banach, Hilbert…) birer nesne olarak görmüş ve aralarındaki anlamlı eşlemeleri (sürekli fonksiyonlar, lineer dönüşümler vb.) oklar (morfizmler) olarak ele almıştır. Bu kuşbakışı perspektif, matematiğin farklı dallarında tekrar eden temel yapıları ve ilişkilerin kolayca incelenmesini sağlamıştır. Örneğin, uzaydaki iki nesnenin çarpımı, Kümeler kategorisinde bildiğimiz kartezyen çarpım, Vektör Uzayları kategorisinde direkt çarpım, Topolojik Uzaylar kategorisinde ise çarpım topolojisi ile donatılmış X × Y uzayı olarak karşımıza çıkmaktadır.

Kategori teorisi, mevcut matematiksel yapılar arasındaki evrensel ilişkileri aydınlatırken, hemen hemen aynı zamanlarda, uzay kavramının en temel taşı sayılan nokta fikrine meydan okuyan daha da köklü bir sorgulama başlamıştır. Nokta- Bağımsız Topoloji (Point-free Topology) veya daha teknik adıyla Lokal Teori olarak bilinen bu yaklaşım, uzayı, onu oluşturan noktaların bir toplamı olarak görmek yerine, içindeki bölgelerin (açık kümelerin) ve bu bölgelerin birbirleriyle olan ilişkilerinin (kapsama, kesişme, birleşme gibi) oluşturduğu bir yapı olarak tanımlamayı önermiştir. Bu fikrin kökleri, Stone‘un, topolojik uzaylardaki açık kümeler ailesinin cebirsel yapısı ile Boole cebirleri arasında derin bir ilişki olduğunu keşfetmesine dayanır. Daha sonra Isbell, Johnstone gibi matematikçiler bu fikri geliştirerek, noktaların ikincil veya türetilmiş olduğu, asıl temel olanın bölgelerin mantığı (locale) olduğu bir teori inşa etmişlerdir.

Bu fikir ilk başta kulağa çok soyut gelebilir, ama gündelik sezgilerimizle de örtüşen yönleri vardır. Hiç hayatınızda fiziksel olarak boyutsuz bir nokta gördünüz mü? Bir kağıda bıraktığınız en küçük kalem izi bile, mikroskop altında bakıldığında belirli bir alana sahip bir leke olarak görünecektir. Fiziksel dünyamızda temel olanlar aslında noktalar değil, bölgeler, alanlar ve hacimlerdir. Noktasız topoloji, matematikçilerin “Acaba matematiksel evrenimiz de, en temelinde, bu fiziksel sezgiye daha mı yakın?” sorusuna verdikleri bir cevap olarak görülebilir.

Uzay kavramının tarihsel gelişimi, insanlığın dünyayı anlama ve modelleme çabasının bir yansımasıdır. Bu kavram, basit geometrik şekillerden en soyut matematiksel yapılara kadar uzanan bir yolculukta evrilmiştir. Antik çağda tarla ölçümüyle başlayan serüven, bugün kuantum alanlarının ve sonsuz boyutlu uzayların analizine kadar gelmiştir. Burada belki de en heyecan verici olan, bu yolculuğun henüz tamamlanmamış olmasıdır. Her yeni matematiksel keşif, uzayın gizemli doğasına dair yeni sorular doğurmaktadır.

Einstein’a diyor ki: “İki şey sonsuzdur: evren ve insan aptallığı; ama evren konusunda emin değilim.” Fakat bir matematikçinin gözünde “Üç şey sonsuzdur: evren, insan aptallığı ve matematiksel uzayların çeşitliliği; ama sonuncusundan eminiz!

KAYNAKLAR
1) https://en.wikipedia.org/wiki/Projective_geometry
2) https://plato.stanford.edu/entries/descartes-mathematics/
3) P. Johnstone, Elements of the History of Locale Theory. In: Aull, C.E., Lowen, R. (eds) Handbook of the History of General Topology. History of Topology, vol 3. Springer, Dordrecht, 2001.

Gözle Görülür Bir Gerçek, Asırlık Bir Bilmece: Jordan Eğri Teoremi

Posted on 11 Şubat 2025 by esrakorkmaz

Cevapla

Matematikte bazı gerçekler öylesine bariz ve kolay anlaşılır gibi görünür ki, onları sorgulamak aklımızın ucundan bile geçmez. Ancak konu matematiksel ispata geldiğinde, bu apaçık gerçeklerin ardında, uzun süren mücadeleler, zekice kurgulanmış ispatlar ve bazen de çözülemeyen gizemlerin yattığını fark ederiz. Bunun en bilinen örneklerinden biri “Eğer $n>2$ bir tam sayı ise $x^n + y^n = z^n$ denklemi sağlayan pozitif $x, y, z$ üçlüleri bulunamaz” ifadesiyle bilinen Fermat’nın son teoremidir. Fermat’nın 1640 yılında, yanına iliştirdiği “Bunun gerçekten harika bir ispatını buldum, fakat bu sayfanın kenarı onu yazmak için çok dar!” minvalinde bir not ile matematik dünyasına miras bıraktığı bu muamma, matematikçileri 358 yıl boyunca uğraştırmıştır. Teorem popüler kültürde de oldukça ilgi çekmiş, kitaplarda (Fermat’s Enigma, Fermat’s Last Theorem, Papağan Teoremi), dizi ve filmlerde (Oxford Cinayetleri, La habitacion de Fermat, Fermat’s Last Tango, Simpsons) kendisinden söz ettirmiştir. Diğer bir örnek, herhangi bir haritayı, komşu ülkelerin aynı renkte olmaması koşuluyla, en fazla dört renk kullanarak renklendirebileceğimizi ifade eden dört renk teoremidir. 1852 yılında ortaya atılan bu teorem, ancak 1976’da, 1200 saatlik bilgisayar hesabı yardımıyla kanıtlanana dek çözülememiş bir problem olarak kalmıştır.
Bu iki meşhur teorem aslında, matematiğin aşikâr sandığımız gerçekleri bile ne denli derinlemesine inceleyip kanıtlamaya çalıştığını gösterir. Bu yazımızda, bu durumun bir diğer çarpıcı örneği olan Jordan Eğri Teoremi’nden bahsedeceğiz.

Jordan Eğri Teoremi, Fransız matematikçi Camille Jordan tarafından 1887 yılında ortaya atılmıştır. Teorem, sürekli (herhangi bir boşluk ya da delik içermeyen), kendini kesmeyen ve kapalı, (yani kısaca basit kapalı) bir eğrinin düzlemi iç ve dış olarak adlandırılan iki ayrı parçaya böldüğünü söyler. Burada, “basit kapalı eğri” yerine “Jordan eğri” ifadesini de kullanabiliriz. Bir Jordan eğri, topolojik olarak bir çembere denktir, yani çemberle aralarında bir homeomorfizma tanımlanabilir.

https://mathworld.wolfram.com/JordanCurve.html

Kulağa çok açık ve net geliyor değil mi? Sonuçta bir çember çizdiğimizde, çemberin içi ve dışı olmak üzere iki bölge oluşur ve bu bölgeleri tespit etmek gayet kolaydır. Peki ya eğrimiz çember gibi ideal bir eğri değilse? Sonuçta Felix Klein’in de söylediği gibi “Herkes bir eğrinin ne demek olduğunu bilir, ta ki yeterince matematik öğrenip sayısız istisnayı görene kadar.” Klein’i doğrular şekilde, bir Jordan eğrisi çok karmaşık ve hatta hiçbir noktada türevlenemeyen bir eğri dahi olabilir. Örneğin; Şekil 1(a)’daki Knuth-Davis twindragon space-filling fraktal eğrisinin sınırı veya 1(b)’deki $f(z)=z^2-0.742+0.1i$ kompleks kuadratik polinomunun Julia kümesi gibi.

Ya da, içerisini ve dışarısını ayırt etmek oldukça zor olabilir. Örneğin, Fiona Ross’un tek bir çizgiyle oluşturduğu ve bize içeri-dışarı kavramlarını sorgulattığı labirent benzeri çizimlerinde olduğu gibi.

*When we could be diving for pearls*, Fiona Ross, 2011

Hatta her ne kadar günlük hayatta karşılaşmasak da, matematiksel olarak, uzunluğu sonsuz olmasına rağmen pozitif alan kaplayan Jordan eğrileri de tanımlanabilir. Bu eğrilerin en güzel örneği, 1903 yılında William Fogg Osgood tarafından tanımlanan Osgood eğrisidir. Aşağıdaki şekilde bu eğrinin, bir eşkenar üçgenden sonsuz sayıda üçgen dilimi çıkarılarak oluşturulan bir örneğini görebiliriz. (Sonsuz bir eğri olduğundan, çizimin, bu eğrinin kendisi değil, bir yaklaşımı olduğunu unutmayalım!)

Osgood eğrisi, https://en.wikipedia.org/wiki/Osgood_curve

Normalde bir çizgiyi/eğriyi düşündüğümüzde, onun genişliğini ihmal eder ve dolayısıyla alanını sıfır olarak kabul ederiz. Osgood eğrisini ilginç kılan, eğrinin çevrelediği alanın değil, eğrinin kendisinin kapladığı alanın pozitif olmasıdır. Fakat burada her ne kadar ‘alan’ kelimesi kullanılmış olsa da, pozitif alan kaplamak ile kast edilen, eğrinin pozitif bir Lebesque ölçüsüne sahip olmasıdır.

Tam bu noktada, konudan biraz sapmayı göze alıp, bu Lebesque ölçüsü meselesine ufak bir açıklık getirelim. Biliyoruz ki, bir çubuğun uzunluğunu ölçerken başlangıç ve bitiş noktalarını belirleriz ve aradaki mesafeyi hesaplarız. Örneğin, [0,1] aralığının uzunluğu 1 birimdir. Fakat bu yöntem bazı durumlarda işe yaramaz. Örneğin, bir noktanın uzunluğu sıfırdır. Bu durumda sayılabilir ya da sayılamaz sonsuzlukta noktadan oluşan bir küme nasıl ölçülür? İşte burada Lebesgue ölçüsü devreye girer. Lebesgue ölçüsü, büyüklük veya uzunluk kavramını genelleştirerek, klasik ölçünün yeterli olmadığı, karmaşık ve hatta bazen patolojik kümelerin ölçümünü daha tutarlı ve kullanışlı bir şekilde ele almanın bir yolunu sunar. Tabii bu genelleştirme yapılırken, herhangi bir kümenin ölçüsünün negatif olmaması, kümeyi belirli bir miktar kaydırdığımızda ölçüsünün değişmemesi gibi, bir ölçümden beklediğimiz bazı sezgisel özelliklerin korunmasına da dikkat edilmiştir.

Lebesgue ölçüsünü, kümeyi aynı özelliğe sahip noktaların oluşturduğu alt kümelere ayırıp, ardından bu alt kümelerin uzunluklarını (veya genel olarak ölçülerini) toplayan bir sistem olarak düşünebiliriz. Örneğin, [0,1] aralığından başlayarak, her aralığın orta üçte birinin yinelemeli olarak çıkarılmasıyla oluşturulan Cantor kümesini ele alalım.

Kaynak:https://brilliant.org/wiki/cantor-set/

Çıkarılan her bir parçanın uzunluğunu toplayarak oluşturulan sonsuz seriden yararlanarak, Cantor kümesinin Lebesque ölçüsünü bulmak mümkündür.
Ya da, sayılabilir bir küme olan $[0,1]\cap \mathbb{Q}$ kümesinin ölçümünün sıfır olması ve bu nedenle [0,1] aralığındaki irrasyonel sayılar kümesinin ölçümünün 1 olması gibi sonuçlara ulaşmak da mümkündür.

Yeniden Osgood eğrisine dönecek olursak, pozitif alan meselesini, sonsuz uzunlukta bir ipi sürekli zikzaklar çizerek yerleştirdiğimizde, küçük de olsa bir alan yaratmasını sağlayabilecekmişiz gibi hissetmemize benzetebiliriz. Osgood eğrisini elde ederken tekrarlanan üçgen çıkarma işlemi sonsuza kadar sürdüğünden, eğrinin sınırları giderek daha fazla alanı kaplayacak ve aradaki boşluklar azalacakmış gibi düşünebiliriz.

Gördüğümüz gibi Jordan’ın teoreminin kapsamına giren böyle ilginç eğrilerin olması, işleri oldukça karışık bir hale getirebiliyor. Dolayısıyla, teoremin tamamlanmış ispatlarında kullanılan homoloji veya cebirsel topolojik kavramlar bir yana, modern topolojinin bile tam anlamıyla isminin koyulmadığı yıllarda bunlarla uğraşan Jordan’ın işi aslında bir hayli zor görünüyor. Zaten yapmış olduğu ispatın, her ne kadar sezgisel olarak doğru görünse de, modern anlamda tüm olası Jordan eğrilerini kapsayan eksiksiz bir ispat olmadığı düşünülüyor. (İspat hakkındaki iddiaları merak edenler buradan devam edebilirler.) Çünkü Jordan, her noktasında türevlenebilir olan (düzgün/smooth), fraktal benzeri yapılar oluşturmayan sorunsuz eğrilerle çalışmıştır.
İspatında ise iç-dış ayrımı yapmak için şu yöntemi kullanmıştır: Eğrinin üzerinde olmayan bir nokta aldığımızı düşünelim. Noktamızdan sonsuza doğru bir ışın gönderelim. (Tutarsızlığı önlemek için, ışınları çizerken sabit bir yön belirleyip tüm noktalar için o yönü kullanmayı tercih edebiliriz.) Şimdi, bu ışınımızın, eğriyle kaç kez kesiştiğini sayalım. Işının eğriyi tek sayıda kesmesi noktanın içeride, çift sayıda kesmesi dışarıda olduğunu gösterir. (Çember üzerinde yapacağımız basit bir testle bunu kolayca görebiliriz.) Eğer çizgimiz bir tepe noktasına dokunuyorsa, işler biraz karışır. Eğrinin o tepe noktasına giren iki kenarı da ışınımızın aynı tarafında kalıyorsa, bunu bir kesişme olarak saymayız. Kenarlar farklı tarafta kalıyorsa sayabiliriz. Örneğin aşağıdaki şekilde seçilmiş olan $x$ noktasından çizilen ışınlar Jordan eğrisini çift sayıda keser. Altta çizdiğimiz (mor ışın) 7 noktada kesiyor gibi görünse de, kırmızı kesişme noktasında, eğrimizin iki kolu da ışının aynı tarafında (sağında) kaldığı için bunu bir kesişme olarak sayamayız. Dolasıyla $x$ noktası eğrinin dışında bir noktadır.

Jordan’dan yıllar sonra 1905’te Oswald Veblen, Jordan Eğri Teoremi için daha sağlam bir ispat sunmuştur. Jordan’ın ispatındaki boşlukları fark eden Veblen, eğrinin düzlemi iki ayrı bölgeye ayırdığını göstermek için topolojik yöntemler kullanmıştır. Veblen, düzlemi üçgenselleştirme gibi teknikler kullanarak, eğrinin iç ve dış bölgelerini daha detaylı bir şekilde analiz etmiş, bu bölgelerin bağlantılılık özelliklerini açığa çıkarmıştır. Çalışmasında, teoremin ispatını önce poligonlar üzerinde vermiştir. Sonra, genel Jordan eğrilerine poligonlarla istenildiği kadar iyi bir şekilde yaklaşılabileceğini ve süreklilik kavramı yardımıyla, poligonlarla yaklaşılan eğrilerin özelliklerinin, genel Jordan eğrisinin özelliklerine yakınsadığını göstermiştir. Böylece, poligonlar için ispatlanan teoremin, genel duruma genelleştirilebilmesi mümkün olmuştur. Tüm bu yaklaşımlarıyla Veblen, teoremin ilk kesin kanıtını veren kişi olmuştur fakat yine de ispat tüm Jordan eğrilerini kapsamaz.
Görüldüğü gibi teoremi tam olarak kanıtlamak için matematikçiler uzun bir süre ter dökmüştür. Jordan’ın ilk denemesiyle başlayan bu matematiksel macera, de la Vallée Poussin, Schoenflies, Brouwer, Alexander, Kerékjártó ve Denjoy gibi dönemin önde gelen matematikçilerinin kolları sıvayıp, topoloji, kompleks analiz ve geometri gibi farklı alanları harmanlayarak bu sezgisel ama bir o kadar da girift teoremi kanıtlamaları ile devam etmiştir. Ayrıca, Filippov‘dan Tverberg‘e, Narens‘ten Thomassen‘e kadar birçok matematikçi, standart olmayan analizden (nonstandard analysis) Brouwer sabit nokta teoremine, yapısal (constructive) matematikten çizge teorisine kadar farklı yaklaşımlarla yeni ve daha basit kanıtlar üretmeye devam etmişlerdir.

Jordan Eğri Teoremi, topolojinin temel taşlarından biri olmanın çok ötesinde, modern matematik ve mühendisliğin sayısız uygulamasında sessizce işleyen bir prensiptir. Günlük hayatta karşımıza çıkmasa da, teoremin sağladığı iç-dış ayrımı prensibi, bilgisayar grafikleri, robotik, coğrafi bilgi sistemleri gibi çeşitli alanlarda dolaylı olarak kullanılır. Ancak asıl büyüleyici olan, bu teoremin, matematiğin bizi bazen nasıl şaşırtabileceğine dair çarpıcı bir ayna tutmasıdır. Bizleri, sezgilerimizin bizi yanıltabileceği, en basit görünen soruların bile karmaşık cevaplar içerebileceği ve matematiksel ispatın, bizi kesinliğe ve derin anlayışa ulaştıran yegane araç olduğu gerçeğiyle yüzleştirir. Ve son olarak bize şunu hatırlatır: İnsanlığın, “apaçık” olanın ötesindeki sır perdesini aralama tutkusu, hiç kuşkusuz sonsuza dek devam edecektir.

KAYNAKLAR
1) https://www.maths.ed.ac.uk/~v1ranick/jordan/index.htm
2) https://www.maths.ed.ac.uk/~v1ranick/jordan/maehara.pdf
3) https://facultystaff.richmond.edu/~wross/pdf/Jordan.pdf
4) https://www.uni-ulm.de/fileadmin/website_uni_ulm/mawi.inst.020/sauter/files/Sauter-TwistedJordan.2017.usem20.pdf
5) https://brilliant.org/wiki/cantor-set/
6) https://www.math.unm.edu/~crisp/courses/math402/spring16/CantorSet.pdf
7) https://nebusresearch.wordpress.com/2016/07/07/theorem-thursday-the-jordan-curve-theorem/
8) P. Coggins, Active learning for development of a conceptual understanding of the jordan curve theorem for preservice elementary education majors and non-mathematics majors, 12th annual International Conference of Education, Research and Innovation, 2019.
9) O. Veblen, Theory on Plane Curves in Non-Metrical Analysis Situs. Transactions of the American Mathematical Society, 6(1), 83–98, 1905.

Cebimizdeki Matematik: GPS, Doğrusal Cebir ve Kozmik Denklemler

Posted on 12 Kasım 2024 by esrakorkmaz

Cevapla

Telefonunuzu çıkarıp en yakın kahve dükkanını her aradığınızda, farkında olmadan matematiğin en zarif uygulamalarından birine tanık oluyorsunuz. Haritalar uygulamanızı açtığınızda, ekranınızda beliren o mavi nokta aslında bir sihir değil, sadece hareket halindeki matematik. Size nerede durduğunuzu söyleyebilmek için gerçek zamanlı olarak binlerce denklemi çözüyor. Başınızın kilometrelerce üzerinde, hassas mühendislikle üretilmiş uydularda atomik saatler çalışıyor ve her biri atmosfer boyunca sinyaller yayıyor. Akıllı telefonunuz uzaydan gelen bu fısıltıları yakalıyor ve bu bilgiyi, dünya üzerindeki konumunuza dönüştürüyor. Tüm bu kozmik orkestranın şefi ise “Doğrusal Cebir”.

GPS günümüzde elektrik veya su gibi sıradan bir hizmet olarak görülüyor. Ancak bu basit ara yüzün altında, eski çağlardaki denizcileri hayrete düşürecek matematiksel bir harika yatıyor. Onlar usturlab ve yıldızlara güvenirken, biz konumumuzu hassasiyetle belirlemek için doğrusal denklemleri, matris dönüşümlerini ve özdeğerleri (eigenvalues) kullanıyoruz. Bu yazıda, uydular yardımıyla mesafe ölçmek gibi temel bir fikrin, doğrusal cebirle çözülebilecek bir probleme nasıl dönüştüğünü inceleyeceğiz.

Günümüz GPS alıcıları birçok farklı konumlandırma tekniği kullanır. Her tekniğin matematiği biraz farklı olsa da, hepsinin temelinde trilaterasyon yöntemi yatar. Trilaterasyon, koordinatları bilinen noktalardan, uzaklıkları ölçerek konum belirleme yöntemidir. Bunu günlük hayattan bir örnekle açıklayalım:
Bir şehirde kaybolduğumuzu ve üç farklı kişiye, onlardan ne kadar uzakta olduğumuzu sorduğumuzu düşünelim. A, B ve C kişileri bize, onlardan sırasıyla 3, 4 ve 3.5 metre uzakta olduğumuzu söylesinler.

Sadece bu bilgiyle, bir harita üzerinde üç çember çizerek tam olarak nerede olduğumuzu anlayabiliriz. Bunun için, A kişisinin etrafında 3, B kişisinin etrafında 4 ve C kişisinin etrafında 3,5 metre yarıçaplı birer çember çizersek, bu üç çemberin kesiştiği nokta tam olarak bizim konumumuzdur. İşte bu aslında GPS’ in çalışma şeklidir. Tek bir farkla; 3 boyutlu uzayda insanlar yerine uydular kullanılır.

Her bir uydu sürekli olarak iki temel bilgi gönderir: Kendi konumu ve sinyalin gönderilme zamanı. Sizin GPS alıcınız ise bu sinyalleri alır, sinyali ne zaman aldığını not eder ve ne kadar sürede geldiğini hesaplar. Bu noktada basit ama önemli bir formül, yani yol=hız x zaman formülünü kullanarak aradaki mesafeyi bulabilir. Her GPS uydusu uzayda bir kürenin merkezi gibidir. Bu kürenin yarıçapı ise uydunun bizimle arasındaki mesafeye eşittir. Biraz önceki örnekte olduğu gibi, bu kürelerin kesişimi bize uzaydaki konumumuzu verecektir. Bu noktada şu bilgiyi eklemekte fayda var: GPS üzerine yapılan taptaze bir çalışmaya⁽⁵⁾ göre uzaydaki konumumuzu kesin olarak belirleyebilmek için, 5 veya daha fazla uydudan gelen verinin hesaba katılması gerekir.

https://gisgeography.com/trilateration-triangulation-gps/

Şimdi bir örnek yardımıyla, işlerin nasıl yürüdüğünü anlamaya ve 4 uydu kullanarak konumumuzu bulmaya çalışalım. İlk olarak, deniz seviyesindeki her nokta için $x^2 + y^2 +z^2=1$ formülünün geçerli olduğunu, zaman biriminin milisaniye ve ışık hızının yaklaşık olarak 0.047 dünya yarıçapı/milisaniye olduğunu kabul edelim. Uyduların konumları ve sinyallerin ulaşma süresi ise aşağıdaki gibi olsun:

Şimdi uzaydaki konumumuzun $(x,y,z)$ ve sinyalin bize ulaştığı zamanın $t$ olduğunu varsayalım. Her bir uydu için, uydu ile aramızdaki mesafeyi hem “ışık hızı x zaman” hem de iki nokta arasındaki uzaklık formüllerini kullanarak yazıp birbirine eşitleyelim. Uydu 1 ile başlayalım:

$\sqrt{(x-1)^2 + (y-2)^2 + (z-0)^2}=0.047\times (t-19.9)$ . Burada, her iki tarafın karesini alırsak; $(x-1)^2 + (y-2)^2 + (z-0)^2=(0.047)^2 (t-19.9)^2$ elde ederiz. Şimdi, tüm doğrusal ifadeleri bir tarafta, kuadratik ifadeleri ise diğer tarafta toplayalım ve bu denklemi (E1) olarak adlandıralım:

$2x + 4y - 2(0.047)^2 (19.9)t = 1^2+2^2-(0.047)^2 (19.9)^2 +x^2 +y^2 +z^2-(0.047)^2 t^2$

Uydu 2 için elde edilen (E2) denklemi;

$4x + 4z - 2(0.047)^2 (2.4)t = 2^2+2^2-(0.047)^2 (2.4)^2 +x^2 +y^2 +z^2-(0.047)^2 t^2$

biçiminde olacaktır. Aynı işlemi diğer uydular için de yaparsak, yukarıdaki formatta yazılmış (E3) ve (E4) denklemlerini elde ederiz. İşlem sonunda tüm denklemlerin sağında ortak bir terim olduğu göreceğiz: $x^2 +y^2 +z^2-(0.047)^2 t^2$ . Bu terimden kurtulup, 3 adet doğrusal denklem elde etmek için aşağıdaki işlemleri yapalım. Elde ettiğimiz yeni denklemleri ise (L1),(L2) ve (L3) ile gösterelim:

(L1)=(E2)-(E1), (L2)=(E3)-(E2), (L3)=(E4)-(E3).

Örneğin (E1), $2x-4y+4z+2(0.047)^2 (17.5)t = 3.86206225$ doğrusal denklemidir. Şimdi elimizde 4 bilinmeyen ( $x, y, z, t$ ) ve 3 doğrusal denklem (E1, E2, E3) var. Bu durumda $x, y$ ve $z$ bilinmeyenleri, $t$ ‘ye bağlı olarak bulunabilir. Elde edilen $x, y$ ve $z$ değerlerini, örneğin (E1)’de yerine koyarsak, $t$ ‘ye bağlı kuadratik bir denklem elde ederiz. Buradan elde edilecek iki $t$ değerinden hangisini seçmemiz gerektiğini anlamak için, $t$ ‘yi yerine koyarak bulacağımız $(x, y,z)$ üçlülerinden hangisinin, başlangıçta varsaydığımız $x^2 + y^2 +z^2=1$ eşitliğini sağladığını kontrol edebiliriz.

Tabii ki gerçek hayattaki durum, burada verdiğimiz yaklaşımdan daha da karmaşıktır ve birçok hata kaynağı bulunur. Örneğin, sinyaller iyonosfer tabakasından geçerken yavaşlayabilir ve yön değiştirebilir. Hava durumu, nem oranı sinyal kalitesini etkileyebilir. Atomik saatler her ne kadar hassas olsalar da, küçük zaman hataları büyük konum hatalarına yol açabilir. GPS alıcısının kalitesi, elektronik gürültü ve işlem gücü gibi faktörler ölçüm hassasiyetini etkileyebilir. Hatta uyduların yörüngelerinde küçük sapmalar bile olabilir.
Tüm bu faktörler nedeniyle, günlük hayatta kullandığımız GPS cihazları genellikle birkaç metrelik hata payıyla çalışır ve daha hassas konum belirlemesi gereken durumlarda ek düzeltme sistemleri kullanılması gerekebilir. Örneğin, GPS’in konum doğruluğunu değerlendiren hata matrislerinde, özdeğerler (eigenvalues) yardımıyla konumlandırma hataları ve belirsizlikleri en aza indirgenmeye çalışılır.

Tüm zorluklara rağmen, GPS teknolojisi sürekli gelişmeye devam ediyor. Araştırmacılar daha hassas ölçümler için yeni matematiksel modeller geliştirirken, mühendisler daha güçlü sinyal işleme teknikleri üzerinde çalışıyor. Burada belki de en etkileyici olan, gündelik hayatımızda farkında bile olmadan kullandığımız bu sistemin, aslında yüzyıllar boyunca matematikçilerin soyut dünyalarında geliştirdikleri fikirlerin bir ürünü olması. Doğrusal cebir gibi teorik bir matematiğin, milyarlarca insanın hayatını kolaylaştıran somut bir teknolojiye dönüşmesi, bilimin evrensel dilinin gücünü gösteriyor.

KAYNAKLAR
1) https://tomrocksmaths.com/wp-content/uploads/2023/06/sunny-miao_-mathematical-approaches-to-global-positioning-systems.pdf
2) https://www.math.kent.edu/~reichel/courses/intr.num.comp.1/fall13/lecture4/project1.pdf
3) B. Kolman, D. A. Hill, Elementary Linear Algebra with Applications: Pearson New International Edition, 9th edition, 2013.
4) https://www.aeronomie.be/en/encyclopedia/ionosphere-influence-satellite-communication-gps
5) M. Boutin and G. Kemper. Global positioning: The uniqueness question and a new solution method. Advances in Applied Mathematics (2024).
6) https://gisgeography.com/trilateration-triangulation-gps/

Bir Fincan Kahveden Mutlak Gerçeklere : İspat Teknikleri Üzerine

Posted on 11 Eylül 2024 by esrakorkmaz

Cevapla

Matematiği diğer birçok bilimden farklı kılan şey nedir? Bu soruya yanıt vermek için önce, şimdiye kadar yazılmış en başarılı kitaplardan biri olan Öklid’in Elementlerinden ve onu zamandan bağımsız kılan özelliğinden bahsetmemiz gerekir.

Bildiğimiz gibi matematik ilk zamanlarda insanların ihtiyaçları doğrultusunda şekillenmiştir. Arazi ölçümleri, arenaların, su depolarının ve diğer pratik projelerin tasarımı için geometri ve trigonometri sorularının ele alınması gayet doğaldır. Kuşkusuz ki, üçgen, kare, dikdörtgen ve çember gibi kavramlar bu bağlamda doğal bir şekilde ortaya çıkmıştır.

Örneğin kareyi ele alalım: Ensiz ve herhangi bir kıvrılma/pürüz içermeyen 4 çizgiden oluşan bir şekil. Fakat burada, gerçeklikle örtüşmeyen bazı durumlar var. Yaşadığımız gezegenin geometrisi göz önüne alındığında, bu denli kusursuz bir şekli oluşturmak mümkün olabilir mi? Diğer taraftan, kağıt üzerine kalemle bir çizgi çizdiğimizde, genellikle çizginin genişliği olmadığını düşünürüz. Fakat aslında, kalemle yapılan herhangi bir fiziksel işaret, kalem ucunun boyutu veya mürekkebin kalınlığı nedeniyle bir miktar genişliğe sahip olacaktır.

Dolayısıyla, kare, çember, dikdörtgen vs. yalnızca idealize edilmiş birer kavram, yani birer tanımdan ibarettir. Matematik ise, tüm bu tanımlardan ve kabullerden yola çıkarak yeni doğrular elde etme sanatıdır. İşte bu doğrular silsilesinin temelini atan Öklid olmuştur. Bunun için işe nokta, doğru gibi bazı kavramların tanımıyla başlamıştır. “Doğru, ensiz bir uzunluktur” gibi. Sonra, adına postulat (belit) denilen su götürmez gerçeklerle yola devam eden Öklid, ortaya, bunları temel alan bazı iddialar atmıştır. (Bu tarz iddialara önerme de diyebiliriz.) İşte ortaya atılan bu iddiaların günümüzde hala geçerliliğini korumasını ve aslında, matematiğin eşsiz ve zamansız olmasını sağlayan şey ispatlardır.

İspat kavramının tarihi oldukça belirsizdir. Her ne kadar, modern standartlara uygun olmasa da, kayıtlara geçen ilk matematiksel ispat Babillilere aittir. Babilliler (Çinlilerle birlikte) Pisagor teoreminin Pisagor’dan çok daha önce farkına varmışlardı ve teoreminin neden doğru olduğunu gösteren bazı diyagramlara sahiptiler. Yine Öklid öncesi dönemde, Pisagor matematiksel, özellikle de geometrik ifadelerin, kesin ispat yoluyla doğrulanması gerektiğini vurgulamıştır. Tabii ki, kendi ismiyle anılan meşhur teoremi ispat etmiştir. 19. yüzyıldan başlayarak altın çağını yaşayan ispatlama yöntemi, biliyoruz ki halen matematiğin temelidir.

Peki ispat yapabilmek için ne gerekir? İlk olarak, matematiğin de tüm diğer diller gibi bir yapısı ve kuralları unutmamamız ve bu dili en azından bir öykü yazabilecek kadar öğrenmemiz gerekir. Sonrasında ise biraz ilham ve biraz da teknik yardımıyla sonuca ulaşmaya çalışırız. Şimdi, çok da kitabi bir anlatıma girmeden, daha çok örnekler üzerinden birkaç yöntem inceleyelim.

1) İspat yaparken, aslında bir kurgu oluşturduğumuzu ve bu kurgunun bir “giriş”, “gelişme” ve “sonuç” kısmı olması gerektiğini unutmayalım. Şimdi aşağıdaki örnek üzerinde bu kurguyu görmeye çalışalım:
Örnek: $f:A \rightarrow B$ ve $g: B \rightarrow C$ birer fonksiyon olmak üzere, $f$ ve $g$ bire-bir ise $g\circ f: A \rightarrow C$ de bire-birdir.
*Giriş: Bu kısmı, ‘elimizdeki veriler’ kısmı olarak düşünebiliriz. Sahip olduklarımız, bileşke tanımı, bire-birlik koşulu (yani, $h(a)=h(b) \Rightarrow a=b$ ) ve $f$ ile $g$ ‘nin bire-bir olması.
*Gelişme: Bu kısımda amacımıza yoğunlaşalım. Görmek istediğimiz şey, her $x,y \in A$ için $(g\circ f)(x) =(g\circ f)(y)$ ise $x=y$ olduğudur. O halde $(g\circ f)(x) =(g\circ f)(y)$ olduğunu kabul ederek ilk adımı atabiliriz. Amaca ulaşmak için, başlangıçta verilen malzemelere ihtiyaç duyarız. İlk olarak bileşke tanımından, $g(f(x))=g(f(y))$ olacaktır. O halde, $g$ bire-bir olduğundan $f(x)=f(y)$ elde edilir. Madem, $f$ de bire-bir, dolayısıyla buradan $x=y$ sonucuna ulaşılabilir.
*Sonuç: $(g\circ f)(x) =(g\circ f)(y)$ olması $x=y$ sonucunu doğurduğundan, $g\circ f$ bire-birdir.
Buradaki en önemli kısım varış noktasını önceden belirlemektir. Gelişme kısmının başında, neyi görürsek ispatın tamamlanacağını belirtip, sonra yola koyuluyoruz. Hani sonundan başlayan bazı filmler vardır. Sonrasında sizi flashback’lerle yeniden aynı sona götürmeye çalışırlar. Burada yaptığımız şey tam olarak bu aslında.

2) Bir ispatta önemli olan sadece doğru adımlar atmak değil, tüm bu adımları doğru sırayla atmaktır.
Örnek: Reel sayılar için cisim aksiyomlarını ve her $x\in \mathbb{R}$ için $x.0=0$ eşitliğini kullanarak $a(b-c)=ab-ac$ eşitliğinin sağlandığını ispatlayalım.
Elimizdeki bilgiler: Cisim aksiyomları, $x-y=x+(-y)$ ve $x.0=0$ eşitlikleri.
Şimdi aşağıdaki iki farklı ispat girişimini inceleyelim. Her ikisi de hemen hemen benzer adımlara sahip olmasına rağmen, yalnızca İspat1 doğru olandır. Çünkü eşitliğin sol tarafı ile başlar ve bizi elimizdeki malzemeler yardımıyla sonuca götürür. İspat2’de ise, gösterilmek istenen şey, daha ispatlanmadan doğru kabul edilmiştir.

3) Bir iddiayı çürütmek (disprove) için ispata ihtiyaç duyulmaz. Örneğin, “mor fil yoktur” iddiasında bulunan birini yalanlamak için, ona bir adet mor fil göstermemiz yeterli olacaktır. Bu çoğu zaman ispat yapmaktan çok daha zor olabilir. Topolojiden basit bir örnek verelim:
Örnek: “Açık kümelerin keyfi arakesiti açıktır” iddiasını ters bir örnek (counterexample) yardımıyla çürütelim. Bunun için $\mathbb{R}$ ‘yi üzerindeki standart/doğal topolojiyle ele alalım. $\forall n\in \mathbb{N}$ için $(-\frac{1}{n}, \frac{1}{n})\subseteq \mathbb{R}$ açık aralıklarının keyfi/sonsuz arakesiti $\bigcap_{n\in \mathbb{N}} (-\frac{1}{n}, \frac{1}{n})=\{0\}$ olduğundan, keyfi kesişim kümesi kapalı bir kümedir.

4) Şimdi de kimi zaman ispata kimi zaman ise bir ters örneğe ihtiyaç duyulan durumlarla devam edelim. “Show/Prove that….” yani, “…. olduğunu gösteriniz” şeklinde bir soru ile karşılaştığımızda, en azından bir ispat tekniği belirleyip işe koyulabiliyoruz. Ama aşağıdaki örneklerde, aslında ilk olarak cevabın ne olduğunu sezgisel de olsa bulup, ona göre aksiyon almamız gerekiyor.
(a) Her sürekli fonksiyon türevlenebilir midir?
(b) $f: \mathbb{R}\mapsto \mathbb{R}$ sürekli, örten ve $K\subseteq \mathbb{R}$ bağlantılı olsun. Bu durumda $f(K)$ bağlantılı mıdır?
(c) $(0,1)$ aralığı $\mathbb{R}$ ‘ye homeomorfik, yani topolojik olarak eşyapılı mıdır?
(d) $[0,1]$ aralığı $\mathbb{R}$ ‘ye homeomorfik midir?

(a) ile başlayalım. Önce soruya sezgisel bir yaklaşım yapalım ve mesela zikzak şeklinde sürekli bir fonksiyon düşünelim.

Sivri uçlar içeren böyle bir fonksiyonun, her noktada türevlenebilir olmasını bekleyemeyiz. Dolayısıyla bu iddianın doğru olmadığını keşfetmiş oluruz ve artık yapılması gereken şey, bir ters örnek bulmaya çalışmaktır.
(b)‘de iddia edilen gerçeği somut olarak görmek zor olabilir. Özellikle de $\mathbb{R}$ yerine $(X,\tau)$ gibi herhangi bir topolojik uzay üzerinde çalışıyorsak. Konu hakkında önceden bir bilgimiz olmadığında, ufak bir ispat denemesi yapıp, ispatta bir engelle karşılaşıyor muyuz diye bakmayı tercih edebiliriz. İddia yanlışsa, ispatın bir kısmında mutlaka sıkıntı yaşanacak, ek bir varsayıma ihtiyaç duyulacaktır. Bu soruda, verilen iddia doğru olduğu için işler tıkır tıkır ilerler. Fakat, örneğin $f$ ‘nin örten olduğu varsayımı verilmediğinde, ispatta bazı geçişleri yapmak mümkün olmayacaktır.
(c) ve (d) için de, önce tahminler üzerinden bir sonuca varmaya çalışıp sonra ispat/çürütme (prove/disprove) yapmamız gerekir. (İlgilenenler için: Burada $(0,1)$ ve $\mathbb{R}$ ‘nin bağlantılılık, kompaktlık, Hausdorff olma vs. gibi topolojik özelliklerinin farklı olup olmadığını kontrol edebiliriz. (c)’de herhangi bir fark olmaması bizi, bu iki uzay arasında bir homeomorfizma yazmaya itecektir. Fakat (d) ‘de işler pek de yolunda gitmiyor. [0,1]’den bir nokta çıkarmak, her zaman bağlantılılığı bozmazken (örneğin 0’ı ya da 1’i), $\mathbb{R}$ ‘den hangi noktayı çıkarırsak çıkaralım bağlantılılık bozuluyor. Dolayısıyla bu ikisi, topolojik olarak aynı şey değildir.)

5) Şimdi, $p\Rightarrow q$ ifadelerini nasıl ispatlayacağımızı inceleyelim. Bu formda verilen bir teoremi ispatlarken farklı teknikler kullanmak mümkündür. Şimdi aynı örneği 3 farklı ispat tekniği kullanarak kanıtlamaya çalışalım. Örneğe geçmeden önce birkaç bilgi/varsayım ile işe başlayalım.
İlk olarak $\mathbb{R}$ üzerinde limit/yığılma noktası tanımını hatırlayalım:
$A\subseteq \mathbb{R}$ ve $x \in A$ olmak üzere, eğer her $\epsilon>0$ için $B(x,\epsilon)\setminus \{x\} \cap A\neq \emptyset$ oluyorsa, yani $x$ noktasını içeren her açık aralık, $A$ ‘nın, $x$ dışında en az bir elemanını içeriyorsa, $x$ ‘e, $A$ ‘nın bir limit/yığılma noktası denir.
Tüm limit noktalarını içeren bir kümeye, kapalı küme denir.
Örnek: $A,B \subseteq \mathbb{R}$ kümeleri kapalı ise $A\cap B$ kümesi de kapalıdır.
Burada “ $p: A,B \subseteq \mathbb{R}$ kümeleri kapalıdır” ve “ $q: A\cap B$ kapalıdır” önermeleri veriliyor ve bizden $p\Rightarrow q$ ‘nun doğruluğunu göstermemiz isteniyor.

(a) İlk olarak doğrudan ispat yöntemi kullanalım. Bunun için yapmamız gereken, $p$ önermesinin doğru olduğunu kabul edip, $q$ önermesinin doğru olduğunu göstermektir. O halde $A$ ve $B$ ‘nin kapalı olduğunu varsayalım. $A\cap B$ ‘nin kapalı olduğunu göstermek için, bu kümenin keyfi bir $x$ limit noktasını alalım ve kümenin bu limit noktasını içerdiğini, yani $x\in A\cap B$ olduğunu gösterelim.
Öncelikle $x$ , $A\cap B$ ‘nin limit noktası olduğundan, tanım gereği, her $\epsilon>0$ için $B(x,\epsilon)\setminus \{x\} \cap (A\cap B) \neq \emptyset$ dir. Bu eşitsizliği $(B(x,\epsilon)\setminus \{x\} \cap A)) \cap (B(x,\epsilon)\setminus \{x\} \cap B) \neq \emptyset$ biçiminde de yazmak mümkündür. Buradan, $B(x,\epsilon)\setminus \{x\} \cap A \neq \emptyset$ ve $B(x,\epsilon)\setminus \{x\} \cap B \neq \emptyset$ olduğu görülebilir. Demek ki $x$ , hem $A$ hem de $B$ ‘nin limit noktasıdır. $A$ ve $B$ kümeleri kapalı olduğundan, her ikisi de bu limit noktasını içerir, yani $x\in A\cap B$ ‘dir.

(b) Şimdi de, dolaylı kanıt tekniklerinden biri olan kontrapozitif ispat kullanalım. $p\Rightarrow q$ ile $\sim q \Rightarrow \sim p$ (yani, $q^\prime \Rightarrow q^\prime)$ önermelerinin birbirlerine denk olduğunu biliyoruz. Bu nedenle, $p\Rightarrow q$ ‘yu ispatlamak yerine $\sim q \Rightarrow \sim p$ ‘yi ispatlamamız yeterli olacaktır. Bunun için $A\cap B$ ‘nin kapalı olmadığını varsayalım ve $A$ ‘nın ya da $B$ ‘nin kapalı olmadığını gösterelim.
Eğer $A\cap B$ kapalı değilse, $x\notin A\cap B$ olacak şekilde bir $x$ limit noktası vardır. $x\notin A\cap B$ ise $x\notin A$ ya da $x\notin B$ dir. Her iki durumu da inceleyelim: $x\notin A$ ise, $A$ kümesi tüm limit noktalarını içermiyor demektir. (Çünkü $x$ , $A\cap B$ ‘nin, dolayısıyla hem $A$ hem de $B$ ‘nin limit noktasıydı.) Bu nedenle $A$ kümesi kapalı değildir. Benzer şekilde, $x\notin B$ olduğunu varsayarak $B$ kümesinin kapalı olmadığı sonucuna ulaşabiliriz.

(c) Son yöntemimiz, yine dolaylı kanıt tekniklerinden biri olan olmayana ergi/çelişkiye varma (contradiction) yöntemi. Bu yöntemi kullanırken, önce $p$ önermesinin doğru olduğunu varsayıyoruz. Doğru olduğunu göstermek istediğimiz $q$ önermesinin ise yanlış olduğunu varsayıp çelişkiye varmaya çalışıyoruz. Yani aslında, $q$ ‘nun yanlış olduğu varsayımı, başımıza işler açıyor ve olmaması gereken sonuçlar doğuruyor. Bu nedenle biz de $q$ ‘nun doğru olması gerektiği sonucuna ulaşıyoruz.
O halde $A,B \subseteq \mathbb{R}$ ‘nin kapalı olduğunu, fakat tersine $A\cap B$ ‘nin kapalı olmadığını varsayalım. Eğer $A\cap B$ kapalı değilse, en az bir limit noktasını içermediğini, yani $x\notin A\cap B$ olacak şekilde bir $x$ limit noktasının olduğunu söyleyebiliriz. Bu noktadan sonra, (a) ile benzer gelişmeler yaşanacaktır. Yani, $x$ , “ $A\cap B$ ‘nin limit noktası olduğundan her $\epsilon>0$ için $B(x,\epsilon)\setminus \{x\} \cap (A\cap B) \neq \emptyset$ ” ile başlayan çıkarımlar dizinden, “ $x$ , hem $A$ hem de $B$ ‘nin limit noktasıdır” sonucuna ulaşırız. Bu noktada $A,B \subseteq \mathbb{R}$ ‘nin kapalı olduğu varsayımı gereği $x\in A$ ve $x\in B$ elde ederiz. Fakat dikkat edersek $x\notin A\cap B$ olduğunu varsaymıştık. Son elde ettiğimiz durum, bu varsayım ile çelişir. Demek ki, $A\cap B$ ‘nin kapalı olması gerekmektedir ve böylece ispat sonlanır.

6) Son olarak “varlık ispatları” konusuna değinelim. Yani bize, $\exists x P(x)$ formunda bir önerme verildiğinde bunu nasıl ispatlarız? Önce bu önermelere birkaç örnek verelim: “Pozitif tam sayıların küplerinin toplamı olarak, iki farklı şekilde yazılabilen bir pozitif tam sayı vardır“, “ $f, [a, b]\subseteq \mathbb{R}$ aralığı üzerinde sürekli bir fonksiyon olmak üzere, $f(a)< c < f(b)$ ise, $f(x) = c$ olacak şekilde bir $a<x<b$ vardır“.
Bu tarz ifadeleri ispatlamak için, yapısal (constructive) ve yapısal olmayan (non-constructive) olmak üzere iki farklı ispat çeşidi vardır. Yapısal ispatlar, önermeyi sağlayan nesnenin ne olduğununun ya da onun nasıl inşa edileceğinin veya bulunacağının açıkça ortaya koyulduğu bir yöntemdir. Örneğin, yazdığımız ilk örnek için, “1729 sayısı pozitif tam sayıların küplerinin toplamı olarak iki farklı şekilde yazılabilen pozitif bir tam sayıdır ( $1729=1^3+{12}^3=9^3+{10}^3$ )” dediğimizde, aslında yapısal bir ispat ortaya koymuş oluruz.
Bazı durumlarda ise, çözümü açıkça söylemesek bile, burada olduğu gibi nasıl inşa edileceği tarif ederiz. İşte constructive kelimesi de tam olarak buradan gelir.
Yapısal ispatların aksine, yapısal olmayan ispatlar bize çözümün ne olduğu ya da neye benzediği hakkında bir fikir vermez. Yani hiçbir inşa işine girmeden, “evet, bazı teoremler/önermeler gereği böyle bir nesne vardır” der ve ispatı tamamlarız.
Örnek: Her $x$ rasyonel sayısı için, $x\leq n$ olacak şekilde bir $n\in \mathbb{N}$ vardır.
Bunu ispatlamak için, bir $x$ rasyonel sayısı alalım ve tersine, istenilen koşulu sağlayan bir $n\in \mathbb{N}$ olmadığını kabul edelim. Bu durum aslında, bu $x$ sayısının, her $n\in \mathbb{N}$ için $x>n$ özelliğini sağladığı anlamına gelir. O halde, $1\in \mathbb{N}$ olduğundan $x>1$ ‘dir ve böylece $x=a/b$ ( $a,b \in \mathbb{N}, a>b$ ) biçiminde yazılabilir. Ayrıca, $a\in \mathbb{N}$ olduğundan $a> a/b$ dir ve buradan $1> 1/b$ ve böylece $1>b$ elde edilir. Fakat bu durum, $b\in \mathbb{N}$ olması ile çelişir. Bu hallere düşmemizin sebebinin, ispatın başında yaptığımız kabul olduğuna dikkat edelim. Demek ki, istenilen koşulu sağlayan bir $n\in \mathbb{N}$ olmalıdır. Ama nedir, neye benzer bilmiyoruz tabii.
(Bunu yapısal bir ispat kullanarak da göstermek mümkündür. Kabaca, $x=p/q, q\neq 0$ biçiminde yazıp $n=|p|+1$ olarak seçebiliriz.)

Tüm bu teknikleri bilmenin ve uygulamanın yanı sıra, nasıl bir yazım tekniği kullandığımız da oldukça önemlidir. Cümlelere matematiksel sembollerle başlamamak, cümleleri birbirlerine uygun bağlaçlar kullanarak, akıcılığı bozmayacak şekilde bağlamak, kullandığımız her kavramı açıklamak bunlardan sadece bazıları.

İspatlar hakkında söylenecek çok daha fazla şey, incelenmesi gereken çok daha fazla özel durum vardır. Yüzyıllarca ispatlamanın mümkün olmadığı, başına ödüller koyulan çetin cevizler, binlerce sayfalık kanıtlar, ilk olarak meşhur dört renk probleminin ispatlanmasıyla hayatımıza giren bilgisayar-destekli ispatlar…Matematiğin bu zengin ve karmaşık alanında derinliklerine indikçe, ispatların sonuçları doğrulamaktan çok daha fazlasını yaptıklarını fark edebiliriz. İspatlar yalnızca matematiğin değil, düşüncenin en güçlü araçlarından ve doğruya ulaşmanın, şüpheyi bilgeliğe dönüştürmenin en güzel yollarından biridir. Matematikçilerin üzerine düşen ise, Alfréd Rényi’nin de söylediği gibi, bir fincan kahveyi teoremlere, yani şık ispatlarla doğrulanmış mutlak gerçeklere dönüştürmektir.

KAYNAKLAR
1) https://livescience.com/earliest-form-of-pythagorean-triplet
2) https://ananddeopurkar.org/teaching/algebra1/cheng.pdf
3) https://www.math.wustl.edu/~sk/eolss.pdf
4) Richard H. Hammack,. Book of Proof, Open Textbook Library, 2013.
5) https://www.karlin.mff.cuni.cz/~krajicek/nature-scholze.pdf

Yakınsaklık vs Düzgün Yakınsaklık

Posted on 13 Mart 2024 by esrakorkmaz

Cevapla

Fonksiyonlar sadece matematiğin değil, farkında olmasak da günlük hayatımızın en önemli parçalarından biridir. Çünkü, karşılaştığımız sorunları çözmeye yardımcı olan karmaşık sistemler inşa etme özellikleriyle, sayısal dünyamızın temellerini oluştururlar. Soyut kavramları, üzerinde çalışabileceğimiz sayısal verilere dönüştürmemiz için bir yol sağlar, gerçek dünyadaki durumları matematiksel olarak modellememize yardımcı olurlar.

Özellikle matematikle ilgili bir eğitim alıyorsanız, muhtemelen içinde fonksiyonların olmadığı bir tek dersiniz bile olmayacaktır. Sürekli, türevlenebilir, harmonik, analitik, yakınsak, konveks, monoton, simetrik, integrallenebilir ve sınırlı olup olmadıklarını, olurlarsa bize ne gibi kolaylıklar sağlayacaklarını didikler durursunuz. Bu yazıda bahsedeceğim konu, makine öğrenmesinden görüntü işlemeye, kontrol teorisinden sinyal işlemeye kadar geniş bir kullanım alanına sahip olan fonksiyon dizileri ve bu dizilerin noktasal & düzgün yakınsaklıkları. Biliyoruz ki, matematikte bazı kavramlar (süreklilik, yakınsaklık, sınırlılık, integrallenebilirlik vs.) uniform yani düzgün versiyonlara da sahiptir. Sanırım çoğu zaman sıkıntı yaratan şey, bu ikisi arasındaki farkı anlamaktır. Yani bir fonksiyon dizisinin nereye yaklaştığını/yakınsadığını görmekte sıkıntı yaşamasak bile, bu yakınsamanın düzgün olup olmadığını tespit etmekte zorlanabiliriz. Öğrenmeye çalışmaktan bunalmışsanız, pes etmeden, bir deneme de birlikte yapalım.

Matematikte “dizi (sequence)” kavramıyla neyin kastedildiği konusunda aşağı yukarı bir fikir sahibiyseniz, fonksiyon dizilerinin, her bir bileşeni bir fonksiyon olan diziler olduğunu tahmin edebilirsiniz. Yani aslında $(f_n)_{n\in \mathbb{N}}=(f_1, f_2, f_3, \ldots )$ görünümünde bir şey. Şimdi soru şu: Tüm bu fonksiyonları çizebildiğimizi varsaysak, acaba $n\rightarrow \infty$ iken, dizinin spesifik bir $f$ fonksiyonuna yaklaştığını gözlemleyebilir miyiz? Daha matematiksel bir dille ifade etmek gerekirse, bu dizi yakınsak mıdır?

Yukarıdaki şekillerde verilen fonksiyon dizilerinde, $n\rightarrow \infty$ iken, dizinin yaklaştığı bir $f$ fonksiyonu olduğunu görmek mümkündür. Fakat biz burada yine tek bir yakınsama şekliyle yetinmeyecek ve farklı yakınsaklık türleri tanımlayacağız. İşe ilk olarak noktasal yakınsama kavramıyla başlayalım:

Öncelikle, $D\subseteq \mathbb{R}$ olmak üzere, $f_n: D \rightarrow \mathbb{R}$ fonksiyon dizisini ele alalım. Bu dizinin tanım kümesinden bir $a\in D$ noktası seçelim. Dikkat edersek, $({f_1}(a), {f_2}(a), {f_3}(a) \ldots )$ bir reel sayı dizisi olacaktır. Eğer her $x\in D$ için elde ettiğimiz sayı dizisinin yakınsadığı bir $f$ fonksiyonu bulabiliyorsak, yani $\forall x, \lim_{n\to \infty}{f_n}(x)=f(x)$ oluyorsa, ${f_n}$ dizisi $f$ ‘ye noktasal yakınsar (pointwise convergent) denir. Biraz daha teknik bir tanım vermek istersek,
$\forall x\in D, \forall \epsilon >0, \exists N \in \mathbb{N}$ if $n\geq N$ then $|{f_n}(x)-f(x)|<\epsilon$ .
Türkçesi şöyle: Rastgele bir $x$ seçelim. Şimdi bize verilecek her $\epsilon>0$ için, dizinin öyle bir $f_{N}$ terimi vardır ki, işte bu terimden sonra $|{f_n}(x)-f(x)|<\epsilon$ olur, yani ${f_n}(x)$ ile $f(x)$ arasındaki mesafe $\epsilon$ ‘dan küçüktür. Burada her $\epsilon>0$ seçiminin şöyle bir güzel yanı var: $\epsilon$ sayısını ne kadar küçültürsek küçültelim, $({f_n}(x))$ sayı dizisi N. terimden sonra $f(x)$ civarında kümelenmiş oluyor.
Seçilen her $x$ için bir $N \in \mathbb{N}$ bulabiliyoruz, ama bu $N$ sayısı seçilen her $x$ için aynı olmak zorunda değil. Yani örneğin $x=3$ için $({f_1}(3), {f_2}(3), {f_3}(3) \ldots )$ dizisi, 100. terimden sonra $f(3)$ ‘ün çevresinde yığılırken; $x=5$ için, 500. terimden sonra $({f_1}(5), {f_2}(5), {f_3}(5) \ldots )$ dizisi $f(5)$ sayısının etrafında yığılıyor olabilir. Burada aslında, farklı $\bf{x}$ değerleri için elde edilen sayı dizilerinin, limit fonksiyonuna varış hızlarının birbirinden farklı olduğunu söyleyebiliriz.

Bu kadar düzensizlik, efendime söyleyeyim her $\epsilon$ için farklı bir $N$ bulduğumuz yetmezmiş gibi, bir de her $x$ için farklı bir $N$ bulmak size de fazla kaotik gelmedi mi? O zaman şimdi, her bir noktada aynı hızla yakınsamayı garanti edecek yeni bir tanım inşa edelim. Her $\epsilon$ için, öyle bir $N$ sayısı bulalım ki, hangi $x$ noktasını denersek deneyelim, $f_{N}(x)$ sonrasındaki terimler $f(x)$ fonksiyonunun etrafında kümeleniyor olsun. Yani her $\epsilon$ ve her $x$ için iş görecek ortak bir anahtarımız olsun. İşte istenilen bu koşulu sağlayan bir $f(x)$ fonksiyonu varsa, ${f_n}$ dizisi $f$ ‘ye düzgün yakınsar (uniform convergent) denir ve
$\forall \epsilon >0, \exists N \in \mathbb{N}, \forall x\in D$ if $n\geq N$ then $|{f_n}(x)-f(x)|<\epsilon$
biçiminde ifade edilir. Dikkat edersek, düzgün yakınsaklık için öncelikle noktasal da olsa elimizde bir limit fonksiyonu bulmamız, daha sonra bu limit fonksiyonuna yakınsama hızı her noktada aynı mı değil mi diye bir test yapmamız gerekir. Şimdi birkaç örnek üzerinden bu kavramları anlamaya çalışalım ve düzgün yakınsaklığı kontrol edebileceğimiz yöntemleri inceleyelim.

1) $f_n: [0,1] \rightarrow \mathbb{R}, {f_n}(x)=x^n$ fonksiyon dizisini ele alalım. Öncelikle, noktasal bazda düşünüp, dizinin yakınsadığı bir $f$ fonksiyonu var mı, varsa nasıl tanımlı olmalıdır, onu anlamaya çalışalım. $x=0$ için ${f_n}(x)=0$ yani $({f_1}(0), {f_2}(0), {f_3}(0), \ldots)=(0, 0, 0, \ldots)$ ve bu dizinin limiti 0 olduğundan, $f(0)=0$ olmalıdır. $x=1$ için ise, ${f_n}(x)=1^n=1$ yani $({f_1}(1), {f_2}(1), {f_3}(1), \ldots)=(1, 1, 1, \ldots)$ ve bu dizinin limiti 1 olduğundan, $f(1)=1$ olmalıdır. $x\in (0,1)$ için, $\lim_{n \rightarrow \infty} x^n = 0$ olduğuna dikkat edelim. Bu durumda dizimizin
$f(x)= \begin{cases} 0 & x\in (0,1) \\ 1 & x=1 \\ \end{cases}$ fonksiyonuna noktasal yakınsadığını söyleyebiliriz.
Noktasal yakınsaklık cepteyse, şimdi de bu yakınsamanın düzgün olup olmadığını kontrol edebiliriz. Önce sezgisel olarak yorumlamaya çalışalım: Örneğin $x=\frac{1}{2}$ ve $x=1$ noktalarını ele alsak, bu iki nokta için, limit fonksiyonuna ulaşma hızlarının eşit olduğunu söyleyebilir miyiz? Tabii ki hayır, çünkü $x=\frac{1}{2}$ noktasında, dizimizin o noktadaki limite yani $f(x)=0$ ‘a ulaşmak için biraz çaba sarf etmesi gerekirken, $x=1$ noktasında bu çabaya gerek kalmaz. Çünkü zaten bu noktada dizimiz limit fonksiyonuna zaten eşittir. Dolayısıyla, yakınsamanın düzgün olmasını bekleyemeyiz.

Bunu doğrulamak için kullanacağımız yöntemlerden biri şöyle: Eğer her $n\in \mathbb{N}$ için ${f_n}$ sürekli ve yakınsama da düzgün ise, dizinin yakınsadığı $f$ fonksiyonu sürekli olmalıdır. Dolayısıyla eğer dizinin noktasal yakınsadığı $f$ fonksiyonu sürekli değilse, yakınsama da düzgün olmayacaktır. Yukarıdaki örnekte bulduğumuz $f(x)$ fonksiyonu sürekli olmadığından, yakınsama da düzgün değildir.

2) Düzgün yakınsamayı göstermek için kullanılan yöntemlerden bir diğeri de, $\lim_{n\to \infty} \text{sup}_{x\in D} |{f_n}(x)-f(x)|=0$ olduğunu göstermektir. Burada yapılan şey aslında, limit fonksiyonu ile dizideki fonksiyonlar arasındaki maksimum mesafenin sıfıra yaklaşıp yaklaşmadığını kontrol etmektir. Limit sıfır ise, yakınsama düzgündür. Şimdi bu yöntemi aşağıdaki örnekler üzerinde uygulayalım.

a) ${f_n}(x)=\frac{nx}{1+n^2 x^2}$ ( $x\in [0,1]$ ) fonksiyon dizisini ele alalım. İlk işimiz noktasal yakınsaklık araştırması yapmak olacak. Burada $x$ noktasının seçiminden bağımsız olarak, $\lim_{n\to \infty} \frac{nx}{1+n^2 x^2}= \lim_{n\to \infty} \frac{nx}{n(\frac{1}{n}+n x^2)}=\lim_{n\to \infty} \frac{x}{\frac{1}{n}+n x^2}=0$ olur. Demek ki dizimiz $f(x)=0$ fonksiyonuna noktasal yakınsar.
Peki bu yakınsama düzgün müdür? Eğer $f(x)=0$ fonksiyonu sürekli olmasaydı, cevabımız ‘hayır’ olacaktı. Fakat burada süreklilik olduğu için, bu yöntemden bir sonuç almak mümkün değil. O halde yukarıda verilen supremum (sup) yöntemini deneyelim. Bunun için, türev kavramı yardımıyla ${g_n}(x)=|{f_n}(x)-f(x)|=\frac{nx}{1+n^2 x^2}$ fonksiyonunun maksimum değerini bulmaya çalışalım:
${g_n}'(x)=0$ olacak şekilde $x$ değerlerini, yani fonksiyonun kritik noktalarını bulalım: ${g_n}'(x)=\frac{n-n^3x^2}{(1+n^2x^2)^2}=0$ ise $x=\pm \frac{1}{n}$ dir. Fakat üzerinde çalıştığımız aralık $[0,1]$ olduğundan, sadece $x= \frac{1}{n}$ noktasını kullanabiliriz. Şimdi ${g_n}'(x)$ ‘in $[0,\frac{1}{n}]$ aralığında pozitif, $[\frac{1}{n},1]$ aralığında negatif olduğunu gözlemleyelim. Bu durum, ${g_n}(x)$ ‘in $[0,\frac{1}{n}]$ aralığında artan, $[\frac{1}{n},1]$ aralığında ise azalan olduğu anlamına gelir.

Elde ettiğimiz bu tablo bize, $x=\frac{1}{n}$ noktasında bir mutlak maksimum değeri olduğunu, yani $\text{sup}_{x\in [0,1]} |{f_n}(x)-f(x)| = {g_n}(\frac{1}{n})=\frac{1}{2}$ olduğunu söyler. Bu da aslında $\lim_{n\to \infty} \text{sup}_{x\in [0,1]} |{f_n}(x)-f(x)|\neq 0$ olması anlamına gelir. Demek ki buradaki yakınsama, düzgün değildir.

b) ${f_n}(x)=(x-\frac{1}{n})^2$ ( $x\in [-1,1]$ ) fonksiyon dizisini ele alalım. Burada yine, limit alma kuralları yardımıyla, $x$ noktalarının seçiminden bağımsız olarak, $\lim_{n\to \infty}{f_n}(x)=x^2$ olduğunu görebiliriz. Böylece fonksiyon dizimizin $f(x)=x^2$ fonksiyonuna noktasal yakınsadığını söyleyebiliriz. Sırada düzgün yakınsaklığı test etmek var. $|{f_n}(x)-f(x)|=|(x-\frac{1}{n})^2-x^2|=|\frac{1}{n^2}-\frac{2x}{n}| \leq \frac{1}{n^2}+\frac{2}{n}|x|$ ve $|x|\leq 1$ olduğundan $0\leq \text{sup}_{x\in [-1,1]} |{f_n}(x)-f(x)| \leq \frac{1}{n^2}+\frac{2}{n}$ olur. (Bu kısımda, supremum kavramını hatırlamak faydalı olacaktır.) Böylece, $\lim_{n\to \infty} \frac{1}{n^2}+\frac{2}{n}=0$ olduğundan, Sandviç/Sıkıştırma teoreminden, $\lim_{n\to \infty}\text{sup}_{x\in [-1,1]} |{f_n}(x)-f(x)|=0$ elde edilir. O halde, ${f_n}(x)$ dizisi, $f(x)=x^2$ fonksiyonuna düzgün yakınsar.

3) Sıradaki yöntemimiz, aşağıdaki koşulun sağlanıp sağlanmadığını kontrol etmek:

$\exists \epsilon_0 > 0 ; \forall n\in \mathbb{N}, \exists x_n \in D, |{f_n}(x_n)-f(x_n)|\geq \epsilon_0$

Burada amaç, $|{f_n}(x_n)-f(x_n)|\geq \epsilon_0$ olacak şekilde bir $\epsilon_0 > 0$ ve bir $x_n \in D$ dizisi bulmaya çalışmak. Şimdi bir örnekle anlamaya çalışalım.
${f_n}(x)=(\frac{n}{nx+1})$ ( $x\in (0,1)$ ) olsun. İlk aşama her zaman noktasal yakınsaklığın varlığını denetlemek. $\lim_{n\to \infty} \frac{n}{nx+1} = \lim_{n\to \infty} \frac{n}{n(x+\frac{1}{n})}=\lim_{n\to \infty} \frac{1}{x+\frac{1}{n}}=\frac{1}{x}$ . Demek ki fonksiyon dizimiz, $f(x)=\frac{1}{x}$ dizisine noktasal yakınsar.
Düzgün sürekliliği kontrol etmek için, $x_n=\frac{1}{n}$ ve seçersek, $|{f_n}(x_n)-f(x_n)|=|\frac{n}{n.\frac{1}{n}+1}-\frac{1}{\frac{1}{n}}|=|\frac{n}{2}-n|=\frac{n}{2}$ olduğundan $\epsilon_0=\frac{1}{2}$ için yukarıdaki koşulun sağlandığını görebiliriz. ( $n\in \mathbb{N}$ olduğunu kullanarak tabii.) Burada $x_n$ seçiminin nasıl yapıldığı meselesi biraz anlaşılmaz gelebilir. Tek bir atışın istenilen diziye isabet etmesini tabii ki bekleyemeyiz. Bir tam sayı elde etmemizi sağlayacak farklı $x_n$ dizileri deneyip, elde ettiğimiz tam sayıya göre bir $\epsilon_0$ seçimi yapmak, bu kuralı uygulamanın bir yolu olabilir.
Bir alıştırma olarak ${f_n}(x)=\frac{x}{n}$ $(x\in \mathbb{R})$ ve ${f_n}(x)=\frac{n^2 x}{n^4 x^2 +2} (x\in (0,1])$ dizilerinin noktasal yakınsak olduğu $f(x)$ fonksiyonunu bulup, düzgün yakınsak olmadığını da bu yöntemi kullanarak göstermeyi deneyebilirsiniz.

4) Şimdi de şu işin bir adını koyalım 😉 Yani şöyle isimli cisimli bir yöntem, ne bileyim, bir teorem filan kullanacağımız bir yol bulalım. Bunun için, $D$ kompakt bir küme olmak üzere, $f_n: D \rightarrow \mathbb{R}$ fonksiyon dizisi verilsin. Eğer,
(a) Her $n\in \mathbb{N}$ için $f_n$ süreklidir,
(b) $(f_n)$ dizisi $f$ fonksiyonuna noktasal yakınsar,
(c) üstelik bu $f$ fonksiyonu sürekli,
(d) ve hatta $f_n$ dizisi monotondur
koşulları sağlanıyorsa, $f_n$ dizisi $f$ ‘ye düzgün yakınsar der Dini Teoremi. Şimdi bu teoremi ${f_n}(x)=\frac{x}{x^2 +n^2} (x\in [0,1])$ dizisi üzerinde uygulamaya çalışalım. Her bir $f_n$ fonksiyonunun sürekliliği, $\lim_{n\to \infty} \frac{x}{x^2 +n^2}=0$ ve $f(x)=0$ fonksiyonunun sürekli olması ufak bir çabayla görülebilecek gerçekler. ${f_{n+1}}(x)=\frac{x}{x^2 +(n+1)^2} \leq \frac{x}{x^2 +n^2} ={f_n}(x)$ olduğundan monotonlukta da bir sorun yok. O halde, Dini teoreminden, yakınsamanın düzgün olduğu sonucunu çıkarabiliriz.

5) Şimdi biraz daha uçuk yöntemler peşinde koşacağız. Aşağıdaki teoreme bir bakalım:
Eğer $f_n: [a,b] \rightarrow \mathbb{R}$ fonksiyon dizisi (Riemann) integrallenebilir fonksiyonlardan oluşuyor ve $f$ fonksiyonuna düzgün yakıyorsa, $f$ de integrallenebilirdir ve $\lim_{n\to \infty} \int_a^b {f_n}(x) dx = \int_a^b \lim_{n\to \infty} {f_n}(x) dx = \int_a^b f(x) dx$ sağlanır. Yani limit ve integralin sırası değişebilir. Demek ki, integralin ve limitin sırası değişemiyorsa, yani yukarıda yazdığımız eşitlik sağlanmıyorsa, yakınsaklık düzgün olamaz.
O zaman bir örnek: ${f_n}(x)=2(n+1)x(1-x^2)^n (x\in [0,1])$ olsun. ${f_n}(0)={f_n}(1)=0$ dır. $x\in (0,1)$ olduğunda, $n\to \infty$ iken limit almaya çalışırsak, $0. \infty$ belirsizliğiyle karşılaşırız. Bu nedenle de L’ Hospital kuralı yardımıyla limiti 0 olarak buluruz. Demek ki dizimiz $f(x)=0$ fonksiyonuna noktasal yakınsar. Diğer taraftan $\int_0^1 2(n+1)x(1-x^2)^n dx= \left [ -(1-x^2)^{n+1} \right ]_0^1=1$ ve $\int_0^1 f(x) dx=0$ olduğundan, $\lim_{n\to \infty} \int_0^1 {f_n}(x) dx \neq \int_0^1 f(x) dx$ eşitliği sağlanmaz. O halde yakınsama düzgün olamaz.
Kendini denemek isteyenlere, bu yöntemi kullanabilecekleri bir örnek: ${f_n}(x)=\frac{2n^2 x}{(1+n^2x^2)^2}$ ( $x\in [0,1]$ ).

Düzgün sürekliliği göstermek için kullanılabilecek yöntemler bunlardan ibaret değil. Aşağıdaki yöntemler de mümkündür.
6) “her bir $f_n$ sınırlıysa ve $f_n$ dizisi $f$ ‘ye düzgün yakınsıyorsa, $f$ de sınırlıdır” teoremini kullanmak da bir teknik olabilir. Dizideki tüm fonksiyonlar sınırlı iken, noktasal yakınsadıkları $f$ fonksiyonu sınırlı olmuyorsa, yakınsama düzgün olamaz.
7) Düzgün Cauchy kriteri kullanmak ise diğer bir yol olabilir.
8) $f_n: [a,b] \rightarrow \mathbb{R}$ dizisi sürekli ve $f_n$ dizisi $f$ ‘ye düzgün yakınsıyorsa, “ $x_n \rightarrow x \Rightarrow {f_n}(x_n) \rightarrow f(x)$ özelliği sağlanır” teoremini kullanmak da mümkündür. $f_n$ fonksiyonları sürekli ve yani $x_n$ dizisi $x$ ‘e yakınsıyorken, $({f_n}(x_n))$ dizisi $f(x)$ ‘e yakınsamayacak şekilde bir $x_n$ dizisi bulabilirsek, yakınsama düzgün değildir. Örneğin ${f_n}(x)=nx^n(1-x)$ dizisini ele alalım. $x=0,1$ için ${f_n}(x)=0$ olduğundan $f(0)=f(1)=0$ ‘dır. $x\in (0,1)$ için, L’ hospital kuralı yardımıyla $\lim_{n\to \infty} {f_n}(x)= (1-x) \lim_{n\to \infty} \frac{n}{x^{-n}}= (1-x) \lim_{n\to \infty} \frac{1}{-x^{-n}ln(x)}=0$ elde edilir. Yani dizimiz, $f(x)=0$ fonksiyonuna noktasal yakınsar.
Diğer taraftan $x_n=\frac{n}{n+1}$ seçilirse, $(x_n)$ dizisinin 1’e yakınsadığı görülebilir. Fakat, ${f_n}(x_n)= {f_n}(\frac{n}{n+1})=n{(\frac{n}{n+1})}^n(1-\frac{n}{n+1})=\frac{n^{n+1}}{ (n+1)^{n+1}}=\frac{1}{(\frac{n}{n+1})^{n+1}}=\frac{1}{(\frac{n}{n+1})^n}\frac{n}{n+1}$ olduğundan $\lim_{n\to \infty} {f_n}(x_n)=\frac{1}{e}$ ‘dir yani, $({f_n}(x_n))$ dizisi $f(1)=0$ ‘a yakınsamaz. O halde, yakınsama düzgün değildir.

Burada detaylıca bahsettiğimiz yöntemlerden, özellikle ilk ikisi, en sık kullanılanlardır ve $\epsilon-N$ tanımına çok da girmeden işimizi halletmemizi sağlarlar. Son olarak şunu da unutmamak gerekir ki, çoğu konuda olduğu gibi, yakınsaklık konusunda da çözümün anahtarı, birçok örnek üzerinde çalışıp, tecrübe kazanmaktır.

KAYNAKLAR
1) Ludmila Bourchtein, Andrei Bourchtein, Theory of Infinite Sequences and Series, Birkhäuser, 2021.
2) https://people.math.wisc.edu/~angenent/521.2017s/UniformConvergence.html

“Zihinsel İşkence”lerden Bilimsel Devrimlere: Karmaşık Sayılar ve Sıralanamaz Doğaları Üzerine

Posted on 31 Ocak 2024 by esrakorkmaz

Cevapla

Günümüzde fizikten mühendisliğe, biyolojiden istatistiğe kadar pek çok alanda kendine yer bulan karmaşık sayıları anlatmak için, oldukça eskiye gitmemiz gerekiyor. Hikayemiz MS 10-70 yılları arasında İskenderiye’de başlıyor. Heron, muhtemelen İskenderiye Kütüphanesi’ni de içeren bir kurum olan Museion’da, hem öğretici hem de araştırmacı olarak bulunan ve matematik, mekanik, fizik, pnömatik gibi birçok alanda çalışmalar yapan bir hezarfen/polimat. Fakat biz burada onun, aeolipile adı verilen ilk buhar türbini, tiyatro sahneleri için tasarladığı özel efektler, otomatik kapılar, otomatlar ve hatta ilkel robotlar gibi birçok icadını bir kenara bırakıp, yalnızca karmaşık sayılarla olan tesadüfi karşılaşmasından bahsedeceğiz.

Yukarıda gördüğünüz cisim bir frustum, yani kesik bir piramit. Heron, Stereometria adlı kitabında, kesik bir koninin yüksekliğinin $h=\sqrt{c^2-\frac{(a-b)^2}{2}}$ formülüyle hesaplanabileceğini göstermiştir. Tabii formülünü bazı özel değerlerler vererek de test etmiştir. Yaptığı denemelerden birinde $a=28, b=4, c=15$ değerlerini seçerek $\sqrt{-63}$ sonucunu bulan Heron, bizlere negatif bir sayının karekökünü içeren bir hesaplamanın ilk örneğini vermiştir. Kendisinin bu geometrik imkansızlık karşısında ne hissettiğini bilmesek de, nasıl bir yol izlediğini biliyoruz. İnsanlığın bu tür matematiksel canavarları düşünmesine daha yüzyıllar varken Heron’un yaptığı, sonucu $\sqrt{63}$ olarak kaydetmek olmuştur. Genellikle sınav kağıtlarında karşılaştığımız gayet klasik bir tepki 🙂 MS 486 yılında, Heron’un izinden giden Hintli matematikçi Bhaskara Acharya ise “Negatif bir sayının karekökü yoktur, çünkü negatif bir sayı, hiçbir sayının karesi değildir.” demiştir.

Şimdi de zamanı biraz ileri sarıp, matematik düellolarının meşhur olduğu 16. yy İtalya’sına doğru uzanalım. Matematik düellosu da nedir diyenlerin, konumuzla da alakalı olan şu yazıya bir göz gezdirmelerini tavsiye ederim. 1510 yılı civarında, Scipione del Ferro $x^3+px=q$ ( $p>0, q>0$ ) biçimindeki kübik denklemler için bir çözüm yolu bulur. Bu noktada, kolaylık için, baş katsayısı 1 olan ve $x^2$ ‘li terim bulundurmayan bu tür denklemlere depressed cubic denildiğini de eklemeden geçmeyelim. Depressed cubic’lerle baş etmeyi öğrenen Del Ferro, bunu asla yayınlamamış, belki de zamanın ruhuna uygun olarak, bir düelloda kullanmak üzere saklamıştır. Del Ferro’nun bu tür denklemleri çözebildiğini biliyoruz, çünkü bu tekniği, hocasının ölümünden sonra depressed cubic’leri çözebilmesiyle övünen öğrencisi Antonio Maria del Fiore’ye öğretmiştir. Bu çözümleri kullanarak ün kazanmak isteyen Fiore, yine bu denklemler üzerinde çalışan Tartaglia’ya, çözmesi için $x^3+3x^2=5$ ve $x^3+6x^2+8x=1000$ denklemlerini göndermiştir. (Gönderilen soruların aslında, “küpü, karesinin 3 katına eklendiğinde 5 olan sayıyı bulunuz” ve “İkincisi birincisinden 2 fazla olan, üçüncü ise ikincisinden 2 fazla olan ve çarpımları 1000 olan üç sayı bulunuz” olduğuna dikkat edelim.)
Fransızlar yaşadığı şehir olan Brescia’yı yağmaladığında, çenesini ve damağını yaran şiddetli bir kılıç yarası aldıktan sonra, konuşması sebebiyle aldığı Tartaglia, yani “kekeme” lakabıyla anılan Niccolò Fontana, kendi kendini yetiştirmiş ve sürekli olarak entelektüel kimliğini kanıtlamaya çalışan bir matematikçidir. Tartaglia, $x^3+px^2=q$ biçimindeki kübik denklemler için bir çözüm yolu bulur ve Fiore’nin meydan okumasına başarıyla karşılık verir. Bu duruma öfkelenen Fiore, Tartaglia’yı 30 soruluk bir düelloya davet eder. Tartaglia Fiore’ye birbirinden farklı problemler gönderirken, sadece hocasının mirası üzerine yükselmeyi amaçlayan Fiore ise, Tartaglia’ya 30 adet depressed cubic gönderir. Tam bir strateji hatası… Bunun üzerine, depressed cubic’ler için bir çözüm yolu bulan Tartaglia, tabii ki bu düellonun kazananı olur. Bu arada Fiore, Tartaglia’nın gönderdiği hiçbir problemi çözemez.

Tartaglia ve Fiore arasındaki matematiksel atışmanın haberi, Milano’daki Gerolamo Cardano’ya ulaşır. Muhtemelen bazılarınıza çok daha tanıdık gelecek olan Cardano, Tartaglia’ya göre daha iyi koşullara doğmuş ve fizik, kimya, astronomi, biyoloji ve matematik gibi birçok alanda çalışmış bir polimat ve bir tıp doktorudur. Otobiyografisinde anlattığı şekliyle “anı yaşayan, açık sözlü, dini küçümseyen, kıskanç, melankolik, bir casus, emanete ihanet eden, bir şeytan, bir tılsım büyücüsü, nefret dolu, iki yüzlü, sahtekar, iftiracı, ve doğası gereği uyumsuz” biri olan Cardano da kübik denklemleri çözmek üzerine girişimlerde bulunur fakat başarısız olur. Bunun üzerine, sırrını öğrenmek umuduyla Tartaglia’yı kendisini ziyaret etmeye davet eder ve
“Kutsal İncil ve bir centilmen olarak inancım üzerine yemin ederim ki, keşiflerinizi bana anlatırsanız asla yayınlamayacağıma ve gerçek bir Hıristiyan olarak, ölümümden sonra kimsenin anlayamayacağı şekilde şifreli olarak yazacağıma söz veriyorum.”
diyerek gizlilik yemini eder. Bunun üzerine Tartaglia, çözümünü bir şiir yoluyla Cardano’ya iletir.

Cardano ayrıca, $x^3+ax^2+bx+c=0$ denkleminde $x=y-\frac{a}{3}$ değişken değiştirmesi yaparak, bu denklemi bir depressed cubic formuna getirmiş ve böylece genel anlamda bir kübik denklemin nasıl çözüleceğini de bulmuştur. Tartaglia’ya verdiği sözü tutmayıp, bu çözümlere Ars Magna (Büyük Sanat) isimli kitabında yer verdiğinde, hem Fiore hem de Tartaglia’yı geride bırakarak, ismini tarihe “kübik denklemleri çözen kişi” olarak yazdırmış olur. Cardano, kitabının 37. bölümünde negatif kökler konusuna yer vererek, bugün karmaşık ya da hayali sayılar olarak adlandırdığımız şeylerin varlığının farkına varan ilk kişi olmuştur. Toplamı 10, çarpımı 40 olan iki sayı ararken, $5+\sqrt{-15}$ ve $5-\sqrt{-15}$ çözümüne ulaşan Cardano’nun, bu sayıların hiçbir yorumu olmadığını, fakat aritmetiğin böyle ilerlediğini not ederek, bu anlamsızlığı görmezden gelmemesi takdir edilesidir. Yine de bu fikri rahatsız edici ya da zihinsel olarak zorlayıcı bulmuş olan Cardano, yapılan işi “zihinsel işkence (mental torture)” olarak nitelendirmiştir.

Tüm bu olanların ardından, 1572 yılında yayınmış olduğu Algebra (Cebir) isimli kitabında Rafael Bombelli, karmaşık sayıları önemsemekle kalmamış, aynı zamanda bu sayılar üzerine aritmetik kurallar da koymuştur. Kendisi bu yüzden karmaşık sayıların mucidi olarak kabul edilir. Bombelli, Cardano’nun formülünü kullanarak $x^3=15x+4$ denklemini çözerken karşılaştığı $+\sqrt{-1}$ sayısını piu di meno, $-\sqrt{-1}$ sayısını ise meno di meno olarak adlandırmış ve bunları kullanarak $(-\sqrt{-1}-1)^3=2-2\sqrt{-1}$ gibi bazı işlemler yapmıştır. Burada, alakasız görünse de, modern cebirsel gösterimin babası François Viète’yi de anmadan geçmeyelim. Çünkü o olmasaydı, belki de matematiği Bombelli gibi yapmaya devam edecektik:

Meraklısı için şu makale Bombelli’nin diline tercüman olabilir.
Son olarak, bugün kullandığımız $i=\sqrt{-1}$ sembolünü ve matematiğin en güzel formülü olarak bilinen $e^{i\pi}+1=0$ eşitliğini literatüre kazandıran Euler’i ve $i=\sqrt{-1}$ sayısını hayali sayı olarak adlandıran Descartes’i anıp, asıl meselemizi tartışmaya başlayalım. Temel problemimiz şu: Acaba karmaşık sayıları da, reel sayıları ya da rasyonel sayıları sıraladığımız gibi sıralayabilir miyiz? Yani iki karmaşık sayı aldığımızda, bunları kıyaslayabilmemize, birinin diğerinden daha küçük/büyük olduğunu söylememize imkan sağlayan bir kural elde edebilir miyiz?

Bunun için önce birkaç deneme yapalım:
1) $a\leq c$ veya $b\leq d$ ise $a+bi\leq c+di$ şeklinde bir sıralama tanımlayalım. Bu durumda $2\leq 8$ olduğundan $2+5i \leq 8-i$ ve $-1\leq 3$ olduğundan $8-i \leq 1+3i$ olduğunu söyleyebiliriz. Sıralamalar hakkında pek de bir şey bilmiyor olsanız bile, $2+5i \leq 8-i \leq 1+3i$ olduğundan $2+5i \leq 1+3i$ eşitsizliğinin sağlanmasını beklersiniz. Fakat ne $2\leq 1$ ne de $5\leq 3$ olduğundan, bu durum doğru değildir.

2) Peki, $a+b\leq c+d$ ise $a+bi\leq c+di$ olarak tanımlasak nasıl olur?🤔 Bu tanımla, hem $2+5i \leq 8-i$ hem de $8-i \leq 2+5i$ oluyor ve bu da pek mantıklı görünmüyor. Çünkü böyle bir durumda $2+5i = 8-i$ olması beklenir.

3) $a\leq c$ ve $b\leq d$ ise $a+bi\leq c+di$ şeklinde bir tanım yapmak daha mantıklı olacak gibi. Çünkü bu şekilde hem sanal hem de reel kısımda işler yolunda gidiyor. Fakat ne yazık ki bu kez, $2+5i$ ve $8-i$ sayılarını karşılaştırmak mümkün olmuyor. Dikkat ederseniz hem $2+5i \leq 8-i$ hem de $8-i \leq 2+5i$ ifadeleri yanlış oluyor.

4) Acaba oldukça geniş bir kullanım alanı olan sözlük sıralaması (lexicographic order) burada da kurtarıcımız olabilir mi? Önce onu bir hatırlayalım: $a<c$ ya da $a=c$ ve $b\leq d$ ise $a+bi\leq c+di$ . Burada $2+5i\leq 8-i$ ve $0\leq 1-2i$ olduğundan, ilk eşitsizliği $1-2i$ ile taraf tarafa çarptığımızda $(2+5i)(1-2i)\leq (8-i)(1-2i)$ , yani $12+i\leq 6-17i$ olmasını bekleriz, fakat maalesef tanımımıza göre bu doğru olmaz.

Denemelerimiz başarısız olduğuna göre, artık kötü düşünmenin zamanı gelmiş demektir. Acaba böyle bir sıralama tanımlamak için boşa kürek çekiyor olabilir miyiz? Bu meseleye geleceğiz, fakat öncesinde bir sıralamadan neler beklediğimizi bir kesinleştirelim. Bunun için keyfi bir X kümesi üzerinde tanımlanan bir sıralamanın
(1) Her $a\in X$ için $a\leq a$ ,
(2) $a\leq b$ ve $b\leq c$ ise $a\leq c$ ,
(3) $a\leq b$ ve $b\leq a$ ise $a=b$ ,
(4) Her $a,b\in X$ için $a\leq b$ ya da $b\leq a$ ,
(5) $a\leq b$ ise $a+c\leq b+c$ ,
(6) $a\leq b$ ve $0\leq c$ ise $ac\leq bc$
koşullarını sağlaması gerektiğini ifade edelim. İspat için çelişkiye varma yöntemi kullanalım. Yani tersine, karmaşık sayılar üzerinde (1)-(6) özelliklerine sahip bir $\leq$ sıralamasının tanımlanabileceğini varsayalım ve bakalım, bu varsayım başımıza ne gibi sorunlar açacak. İspata başlamadan önce, iki küçük Lemma’ya yani yardımcı teoreme ihtiyacımız olacak.
Lemma (a) Her $z$ karmaşık sayısı için $0\leq z \Leftrightarrow -z\leq 0$ gerektirmesi sağlanır.
Kanıt: Öncelikle bunu zaten biliyoruz diye düşünmeyelim. Çünkü elimizdeki $\leq$ sıralaması, reel sayılar üzerindeki klasik büyük/küçük sıralaması değil, karmaşık sayılar üzerinde kurulmuş bambaşka bir sıralama. Bildiğimiz tek şey, bu sıralamanın (1)-(6) özelliklerini sağladığı. Burada, $\leq$ yerine $\prec, \ll, \sqsubset$ gibi bambaşka semboller de kullanabilirdik ama daha standart bir görünüm için klasik bir sembol tercih ettik.
Şimdi ilk olarak, $0\leq z$ olsun. Bu durumda, eşitsizliğin her iki tarafına $-z$ eklersek, (5) numaralı özellikten $-z\leq 0$ elde ederiz. İspatın diğer yönü de benzer şekilde yapılabilir.
Lemma (b) Her $z$ karmaşık sayısı için $0\leq z^2$ dir.
Kanıt: Burada (4) ve (6) numaralı özellikler kullanılarak ispatı tamamlamak mümkündür.

Şimdi asıl ispatı yapmaya hazırız. Öncelikle Lemma (b)’de $z=1$ alırsak, $0\leq 1$ elde ederiz. (Burada, elimizdeki $\leq$ sıralamasının reel sayılar üzerindeki klasik sıralama olmadığını ve bu nedenle $0\leq 1$ eşitsizliğinin zaten sağlandığını düşünmenin yanlış olduğunu bir kez daha vurgulamak isterim.) Bu durumda Lemma (a)’yı uygulayarak $-1\leq 0$ olduğunu da söyleyebiliriz. Bunu bir kenara yazalım. Şimdi Lemma (b)’de $z=i$ alırsak, $0\leq i^2$ yani $0\leq -1$ elde ederiz.
Geldiğimiz noktada elimizde $-1\leq 0$ ve $0\leq -1$ var. Bu nedenle sıralamamızın sağlaması gereken (3) numaralı özellikten $-1=0$ çelişkisini elde ederiz. Demek ki yola çıkış noktamız doğru değil ve bu nedenle karmaşık sayılar üzerinde klasik anlamda bir sıralama tanımlamak mümkün olamaz.

Yapay zekanın gözünden, paralel bir evrende Cardano & Tartaglia 🙂

KAYNAKLAR
1) D. Angell, Ordering Complex Numbers . . . Not, Parabola, Volume 43 (2), 2007.
2) https://www.moment-expo.com/tr/dergiler/88/makine-tarihi/geleneksel-bilimin-oncusu-iskenderiyeli-heron
3) https://www.paradise.caltech.edu/ist4/lectures/Cardano-Tartaglia_Dispute.pdf
4) https://www.quantamagazine.org/the-scandalous-history-of-the-cubic-formula-20220630/
5) https://mathshistory.st-andrews.ac.uk/Biographies/Bombelli/
6)https://www.math.uri.edu/~merino/spring06/mth562/ShortHistoryComplexNumbers2006.pdf
7)https://en.wikipedia.org/wiki/Fran%C3%A7ois_Vi%C3%A8te#Vi%C3%A8te’s_symbolic_algebra
8) J. Stedall, From Cardano’s Great Art to Lagrange’s Reflections: Filling a Gap in the History of Algebra, European Mathematical Society, 2011.
9) D. Burton, The History of Mathematics: An Introduction, 6th edition, McGraw-Hill Science, 2005.
10) https://medium.com/@shashankydv00/complex-numbers-f89003295923
11) D. J. Winter, Review of A History of Algebra., by B. L. van der Waerden, The American Mathematical Monthly, 95(8), 781–785, 1988.

Feynman’ın Perspektifinden Matematik: Uzaylar ve Genelleştirmeler

Posted on 31 Ağustos 2023 by esrakorkmaz

Cevapla

“The same equations have the same solutions” yani “Aynı denklemler aynı çözümlere sahiptir” demiş 20. yüzyılın tartışmasız en parlak beyinlerinden olan Feynman. Kendisinin Nobel ödüllü bir fizikçi oluşunu, ileri görüşlülüğünü, eşsiz mizahını, “Great Explainer” olarak bilinmesini sağlayan, en karmaşık fikirleri bile oldukça sade anlatabilme yeteneğini de göz önünde bulundurursak, yaptığı çıkarıma vereceğimiz tepki sanırım şöyle olur:

En karmaşık kavramları bile büyük bir sadelikle açıklayabilen Feynman’ın bu ilkesi, aldatıcı bir şekilde basit görünebilir. Fakat aslında bilimin ve evrenin birçok sırrını çözmenin anahtarıdır. İki fiziksel sistem aynı temel denklemler kümesiyle tanımlanabiliyorsa, aynı çözümleri veya sonuçları verecektir. Başka bir deyişle, farklı fiziksel olayların davranışları ve sonuçları, ortak bir matematiksel çerçeve kullanılarak anlaşılabilir ve tahmin edilebilir. Örneğin, Newton’un hareket yasaları, gezegenlerin güneş etrafındaki hareketlerini ve Dünya’daki nesnelerin davranışlarını tanımlamak için kullanılabilir.

Feynman’ın ifadesinin fiziğin ötesinde de sonuçları vardır. Örneğin matematikte soyutlama ve genellemenin gücünü ortaya koyar. Yani aslında, içinde yaşadığımız uzay ve bu uzayın belli kuralları varken, matematikçilerin neden metrik uzaylar, vektör uzayları, topolojik uzaylar gibi elle tutulmayan şeylerle uğraştıkları ve genelleme yaptıkları konusuna bir dayanak oluşturur. Tüm bunları anlamak için, matematikte uzay nedir, nasıl tanımlanır ve ne işe yarar sorularına yanıtlar bulmaya çalışalım.

Matematikte uzay tanımı galaksileri, yıldızları ya da kozmik fenomenleri içermez. Matematik dünyasında “uzay”, bir dizi eleman ve bu elemanlar arasındaki ilişkileri, davranışları tanımlayan bazı ek özellikler içeren matematiksel bir yapıdır. Bu yönüyle “küme” kavramından farklıdır. Çünkü uzayların bir iç yapılanması, yani elemanlar arasındaki ilişkilerin nasıl olacağının, yeni öğelerinin nasıl oluşturulacağının yazıldığı bir anayasası vardır. Örneğin;

Vektör uzayları, “vektör” adı verilen elemanları ve belli kurallara uyması gereken, toplama ve skaler çarpma işlemlerini içeren bir yapıdır.

Metrik uzaylar, belli elemanlar ve bu elemanlar arasındaki mesafe kavramını tanımlayan metrik adında bir fonksiyon içeren bir yapıdır. Metrik dediğimiz, öyle “fonksiyonlar içinde bir fonksiyon” değildir. Negatif olmama, simetri özelliği ve üçgen eşitsizliği gibi bazı beklentilerimizi karşılaması gerekir. İşin ilginç yanı, bu uzaylarda mesafeyi ölçme meselesinin her zaman bir cetvel yardımıyla çözülememesidir.

Örneğin yalnızca dik hareketleri dikkate alan taksi metriğine göre $(x_1, y_1)$ ve $(x_2, y_2)$ gibi iki nokta arasındaki mesafe $|x_2-x_1|+ |y_2-y_1|$ formülüyle hesaplanır. Bu metrik Manhattan metriği olarak da adlandırılır, çünkü taksilerin sadece dik çizgiler boyunca seyahat edebildikleri ve kavşaklarda dik açılı dönüşler yapmak zorunda oldukları Manhattan sokaklarında hareket etme şeklini yansıtır.

Mesafeyi koordinatlar arasındaki maksimum fark olarak ölçen Chebyshev metriğine (maksimum metriği ya da $L_\infty$ metriği olarak da bilinir) göre ise $(x_1, y_1)$ ve $(x_2, y_2)$ noktaları arasındaki mesafe $\text{maks}\{ |x_2-x_1|, |y_2-y_1| \}$ olarak tanımlanır. Kurallara uyulduğu sürece, birçok farklı küme üzerinde birçok farklı metrik tanımlamak mümkündür.

Farklı metrik uzaylarda, bildiğimiz tüm kavramların yepyeni bir anlam kazanacağına dikkat edelim. Örneğin, düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların kümesine çember denildiğini biliyoruz. “Uzaklık” tanımı değiştiğinde, çember dediğimiz şey de aynı formda kalmaya devam etmeyecektir. Bu nedenle $\mathbb{R}^2$ kümesi üzerinde taksi metriğine ve Chebyshev metriğine göre “çember” dediğimiz şey, sırasıyla, bir baklava dilimi ve bir kare görünümünde olacaktır.

Topolojik uzaylar, bir küme ve topoloji adı verilen bir ek yapıdan oluşur. Uzay tanımında bahsettiğimiz kurallar ise “topoloji” tanımında devreye girer. Topoloji, kümemizin alt kümelerinden oluşan ve bazı özel aksiyomları sağlayan bir küme ailesidir. Topolojik uzaylar, herhangi bir mesafeden bahsetmeyip, onun yerine “komşuluk” kavramını koyarak yakınlık kavramını incelemek için oldukça elverişli bir ortam sunar.

Bu listeyi oldukça genişletebilir (iç çarpım uzayları, normlu vektör uzayları, Banach uzayları, Hilbert uzayları vb.) ve hatta aralarındaki hiyerarşiyi farklı şekillerde resmedebiliriz.

Peki tüm bu genellemeleri nasıl yapıyoruz? Bunun için Feynman’ın, fizik yasalarını keşfetmek konusunu açıklarken başvurduğu satranç analojisine bir bakalım:

“Diyelim ki bir satranç oyunu. Oyunun kurallarını bilmiyorsunuz, ancak bazen en azından küçük bir köşeden tahtaya bakmanıza izin veriliyor. Bu gözlemlerden oyunun kurallarının ne olduğunu, taşların hareket kurallarının ne olduğunu anlamaya çalışıyorsunuz. Bir süre sonra, örneğin, tahtada sadece bir fil olduğunda, filin her zaman aynı renk üzerinde ilerlediğini keşfedebilirsiniz. Daha sonra filin bir diyagonal üzerinde hareket etmesine ilişkin yasayı keşfedebilirsiniz ve bu daha önce anladığınız yasayı, yani filin hareket ettiği karelerin renginin koruduğunu açıklar. Bu da bir yasayı keşfedip daha sonra onu daha derin bir şekilde anlamamıza benzer.“

İşte matematiksel genelleştirmeler yapmak ve yeni soyut uzaylar tanımlamak da bir anlamda buna benzer. Fizik kanunlarını keşfetmenin, basit gözlemlerden derin teorilere doğru ilerlemeyi gerektirmesi gibi, matematik de giderek soyutlaşan kavramları keşfetmeye ve bu kavramların uyumlu bir şekilde iç içe geçtiği alanları tanımlamaya çalışır. Örneğin 3-boyutlu uzayda, mesafe dediğimiz şeyin pozitif olduğu, noktalar arası uzaklığın simetrik olduğu (yani, $x$ ile $y$ ‘nin birbirine olan uzaklığı ile $y$ ile $x$ ‘in uzaklığının aynı şey olduğu) gibi gözlemler yaparsınız. Daha sonra bunu, bir genelleme yaparken, yani metrik uzayların yasalarını tanımlarken kullanırsınız. Tıpkı gözlemcinin, fillerin beklenen davranışlarına dayalı bir zihinsel modele sahip olması gibi, matematikçiler de genellikle gözlemlenen örüntülere veya özelliklere dayanarak genelleştirilmiş uzayların zihinsel modellerini geliştirirler.

“Sonra bir şeyler olabilir -her şey yolunda gidiyor, tüm yasalara sahipsiniz, çok iyi görünüyor- ve sonra aniden bir köşede garip bir fenomen ortaya çıkar. Bu yüzden bunu araştırmaya, aramaya başlarsınız. (…) Uymayan şey, en ilginç olan şeydir, beklediğiniz gibi gitmeyen kısımdır. Ayrıca, fizikte devrimler de olabilir. Fillerin renklerini koruduğunu ve köşegenler boyunca ilerlediğini fark ettikten ve herkes bunun doğru olduğunu bildikten sonra, bir gün aniden bir satranç oyununda filin rengini korumadığını, değiştirdiğini keşfedersiniz.“

Şimdi, yerleşik düzene uygun sayısız oyundan sonra, bir filin ilerlediği karenin renginin değiştiği bir satranç oyunuyla karşılaştığınızı hayal edin. Bu beklenmedik olay, fil hareketlerinin genelleştirilmiş uzayına ilişkin anlayışınıza meydan okur. Matematiksel açıdan bu benzetme, genelleştirilmiş bir uzayda istisnalar veya varyasyonlarla karşılaşmak gibidir. Bunun üzerine, bu istisnai durumu da içeren yeni bir uzay tanımlarsınız.

Son olarak matematikte genelleştirmeler yapmanın avantajlarından bahsedelim.

“Birçok farklı fiziksel durum için denklemler tamamen aynı görünüme sahiptir. Elbette semboller farklı olabilir – bir harf diğerinin yerine kullanılır – ancak denklemlerin matematiksel biçimi aynıdır. Bu, bir konu üzerinde çalıştıktan sonra, başka bir konunun denklemlerinin çözümleri hakkında doğrudan ve kesin bilgiye sahip olduğumuz anlamına gelir.” diyor Feynman.
Demek ki yeni uzaylar tanımlama yoluyla genelleştirmeler yapmak, bir alandaki kanıtların diğer birçok alana uygulanabilir olmasını sağlar. Feynman’ın da bahsettiği gibi, semboller, isimler tamamen farklı olsa da, problemimiz aslında var olan bir teorinin bir parçası olabilir. Örneğin kalıcı homoloji (persistent homology) sayesinde, cebirsel topolojide bulunan teoremleri ve sonuçları, yüksek boyutlu verileri analiz etmek ve yorumlamak için kullanabiliriz.
Şehirlerin düğüm (node), yolların da kenar (edge) olduğu karmaşık bir ulaşım ağı düşünün. Bu problemi, düğümlerin konumları, kenarların ise bağlantıları temsil ettiği bir çizge (graph) olarak ele alıp, çizge teorisinde bulunan araçlar yardımıyla rotaları optimize edebilir, en kısa yolları bulabiliriz. Bunun dışında, sosyal ağlar, makine öğrenmesi, kriptografi gibi birçok alanda ortaya çıkan problemleri de çözebiliriz.
Lineer cebirde, vektör uzaylarından gelen kavramları ve tekil değer ayrışımı (SVD) gibi teknikleri, görüntü sıkıştırma teknolojisinde kullanabiliriz. Bu soyutlama sayesinde, görsel bir sorunu matematiksel bir soruna dönüştürerek verimli sıkıştırma yöntemleri elde etmiş oluruz.

Soyut uzaylar bazı temel özellikleri koruyarak çok sayıda sorunu çözmemizi sağlar. Akışkanlar dinamiğiyle uğraşan bir mühendis, yüksek boyutlu verilerdeki örüntüleri inceleyen bir veri bilimciyle aynı ilkeleri kullanabilir. Matematikte uzayların ve genelleştirmelerin güzel olmaları, yalnızca matematiksel zarafetlerinden değil, aynı zamanda disiplinler arasında bir köprü olma potansiyellerindendir.

KAYNAKLAR

Sıralamalar, Yakınsamalar ve Ötesi: Limit Superior ve Limit Inferior

Posted on 9 Temmuz 2023 by esrakorkmaz

Yeni bir kavramla karşılaştığımda, yapmadan duramadığım bir şey var. Onu ilk kim ortaya atmış, atmasaymış biz bugün nelerden mahrum kalırmışız öğrenmeden edemiyorum. Bir mesai harcayacaksak, kendisini tanımam, kimin nesiymiş bilmem gerekiyor sonuçta. Bu çoğu zaman şu sebepten de olabiliyor. Öğrenim hayatım boyunca, “bunu asla öğrenmeyeceğim, sınavda da çıksa umrumda değil” diye inatlaştığım bazı konular vardı. Geri dönüp baktığımda, böyle olumsuz hislerle dolu olduğum konularda, “bu işin sorumlusu kim” dürtüsüyle daha da merakla doluyorum. İşte “Limit Inferior (lim inf)” ve “Limit Superior (lim sup)” da amigdalama adeta bir sakız gibi yapışmış korkuların başında geliyor.

Uzun zaman sonra yine aklıma düşen bu konuda, dostum ChatGPT’nin de ağzını arıyorum: “Sence Lim inf ve Lim sup karışık konular mı?”, “Olmasalardı ne olurdu”, “1. ya da 2. sınıf bir matematik öğrencisi için biraz ağır konular mı?” minvalinde sorularla manipüle etmeye çalışıyorum onu. Tabii asla geri adım atmıyor ve yine kaçak oynuyor. Kendisi bir dil modeliymiş de, kişisel düşünceleri yokmuş da… Fakat bu konuya kendimizi daha çok maruz bırakırsak, karmaşıklığı ortadan kalkarmış. O halde şimdi birlikte, sıralamaların (order) dünyasından dizilere, ve oradan da Lim inf/Lim sup konularına uzanan bir yolculuğa çıkalım.

İlk olarak oldukça kafa karıştırıcı olan “maksimal, minimal, maksimum, minimum, supremum ve infimum kavramlarını anlamaya çalışalım. Bunun için önce kısmı sıralı (partially ordered) bir $(P, \leq)$ kümesi alalım. Kısmi sıralı kümelerde (poset), tam sıralı kümelerden (toset) farklı olarak, kümedeki her iki elemanın birbiriyle kıyaslanmak zorunda olmadığını biliyoruz. Örneğin $P$ , dünyadaki tüm insanların kümesi olsun. $P$ üzerinde “ $x\leq y \Leftrightarrow x=y$ ya da $x, y$ ‘nin atasıdır.” bağıntısını tanımlayalım. Bu bir kısmi sıralama bağıntısıdır. Fakat seçtiğimiz 2 kişiden birinin diğerinin atası olması gerekmediği için, bir tam sıralama bağıntısı değildir.

Maksimal vs maksimum eleman: Eğer $m\leq x$ özelliğini sağlayan her $x\in P$ için $x=m$ oluyorsa, $m$ ‘ ye maksimal eleman denir. Eğer bir maksimal elemansanız, sizden büyük kimsenin olmadığına eminsiniz. Ama kısmi sıralamanın doğası gereği, kıyaslanamadığınız bazı elemanlar olabilir. Yani herkesten büyük olduğunuzu iddia edemezsiniz. İşte bu noktada maksimum eleman devreye girer. Eğer her $x\in P$ için $x\leq m$ oluyorsa, $m\in P$ ‘ye maksimum eleman denir. Maksimum elemansanız, sizden büyük kimsenin olmamasının yanı sıra, küme içindeki her elemandan büyüksünüzdür. Maksimal olmak, bir binanın en üst katında oturmaksa, maksimum olmak, şehirde sizden daha yukarıda yaşayan kimsenin olmamasıdır.

Minimal vs minimum eleman: Yukarıdakine benzer bir ilişki burada da var. Eğer $x\leq m$ özelliğini sağlayan her $x\in P$ için $x=m$ oluyorsa, $m$ ‘ ye minimal eleman denir. Yani, diyelim ki, $m$ bir minimal eleman ve siz $x\leq m$ olacak şekilde bir $x$ elemanı bulduğunuzu iddia ediyorsunuz. $x\leq m$ ifadesinin içinde iki ihtimal olduğunu biliyoruz: $x=m$ veya $x<m$ . İşte tanım gereği, ikinci ihtimal asla geçerli olamaz ve böylece $x=m$ olur. Diğer taraftan, minimum eleman, küme içerisindeki her elemanla boy ölçüşme şansı elde etmiş ve bunun sonunda kümedeki her elamandan küçük olarak bulunmuştur. Yani eğer her $x\in P$ için $m\leq x$ oluyorsa, $m\in P$ ‘ye minimum eleman denir.

Şimdi bir örnek yapalım: $A=\{2, 3, 5, 6, 30, 60, 90\}$ kümesi üzerinde “ $x\leq y \Leftrightarrow x|y$ ” kısmi sıralama bağıntısını tanımlayalım. Bu bağıntıya göre 60 ve 90 birer maksimal elemandır. Çünkü eğer $60\leq x$ ise, yani 60, $x$ sayısını bölüyorsa, $x=60$ olmaktan başka şansı yoktur. Benzer bir akıl yürütmeyi 90 için de yapmak mümkündür. Dikkat edersek, bu kümenin, bu bağıntıya göre bir maksimum elemanı yoktur. Eğer 90’dan şüpheleniyorsanız yanılıyorsunuz, çünkü 60, 90’ı bölmediği için $60\leq 90$ diyemeyiz. Yani 90, bu bağıntıya göre, küme içesindeki her elemandan büyük değildir. Benzer şekilde, minimal elamanların 2, 3 ve 5 olduğunu, fakat kümenin bir minimum elemanı olmadığını söyleyebiliriz.

Bu örnekten ve tanımlardan yola çıkarak aşağıdaki gözlemleri yapmak mümkündür:

(1) Kısmi sıralı bir kümede birden çok maksimal eleman olabilir. Ama maksimum eleman varsa, tektir. Kümenin mutlaka bir maksimum/maksimal elemanı olacak diye bir zorunluluk da yoktur.

(2) Her maksimum eleman aynı zamanda bir maksimal elemandır. Fakat, örnekte de görüldüğü gibi tersi doğru değildir.

(3) Eğer $P$ kümesi tam sıralı bir küme ise, yani her iki eleman birbiri ile kıyaslanabiliyorsa, her maksimal eleman bir maksimum elemandır. Maksimal elemanı, maksimum olmaktan alıkoyan tek bir engel vardı, o da tüm elemanlara karşı büyüklüğünü ispatlayamama durumuydu. Fakat tam sıralı bir kümede hem her elemanla kıyaslandı, hem de tanımı gereği kendisinden daha büyük bir eleman bulunamadı.

(4) Maksimal/maksimum ya da minimal/minimum eleman olma seçimlerine adaylığımızı koyabilmemiz için, küme içinde ikamet ediyor olma koşulumuz vardır. Yani küme içinde olmayan bir eleman, koşulu sağlasa bile maksimal/maksimum ya da minimal/minimum olarak seçilemez. Bu sorunu biraz sonra, supremum ve infimum tanımı ile çözeceğiz, merak etmeyin 🙂

Üst sınır/ Supremum: Yine bir kısmi sıralı $P$ kümemiz ve onun bir $S\subseteq P$ alt kümesi olsun. Eğer, her $s\in S$ için $s\leq x$ olacak bir $x\in P$ varsa, $x$ ‘e, $S$ ‘nin bir üst sınırı denir. Dikkat edin, $S$ ‘nin üst sınırı kümenin içinde olmak zorunda değil. Bu eleman ya da elemanlar, kümeyi kapsayan, yani bağıntının kaynağı olan kümede de olabilir. Örneğin $P=\mathbb{R}$ , $S=(0,1)$ alalım. (Burada reel sayıları, bilinen $\leq$ sıralaması ile düşünüyoruz). 1, 2, $\sqrt{2}$ , $\Pi$ sayılarının her biri, $S$ kümesi için bir üst sınırdır. Fakat bu kadar çok eleman bulmak oldukça kafa karıştırıcı bir durum. Onun yerine bunların en küçüğüne, yani en küçük üst sınıra, özel bir anlam biçelim ve onu supremum olarak adlandıralım. Bu örnekte $x=1$ , $S$ ‘nin supremumu olacaktır. $S=(0,1)$ kümesinin bir maksimum elemanı yoktu. Çünkü $x=1$ elamanı kümede yaşamadığı için aday bile olamaz. Fakat, dikkat edersek, supremum olma koşulları arasında küme vatandaşı olma şartı yoktur. Bu durumun bize, integral, serinin yakınsaklık yarıçapı, kümeler arası uzaklık ve Legendre dönüşümü gibi bazı özel tanımlamalara olanak sağlama gibi faydaları olacaktır.

Alt sınır/İnfimum: Şimdi de, “elimdeki küme sınırlı gibi görünüyor, fakat sınırı kümenin içinde değil” problemine yapıcı çözümler sunan infimum tanımına bakalım. İşin mantığı aynı. Öncelikle, her $s\in S$ için $x\leq s$ olacak bir $x\in P$ varsa, $x$ ‘e, $S$ ‘nin bir alt sınırı denir. Eğer $P=\mathbb{R}$ ve $S=(0,1)$ alırsak, $P$ içerisinde, $x\leq 0$ koşulunu sağlayan her $x$ sayısının, $S$ ‘nin bir alt sınırı olduğunu söyleyebiliriz. Bu kez, teklik takıntımıza derman olacak elaman olarak, bunların en küçüğünü seçmenin anlamsız olduğunu fark ediyorsunuzdur sanırım. O halde, $S$ ‘nin her $x$ alt sınırı için $x\leq b$ özelliğini sağlayan $b$ alt sınırına, $S$ ‘nin infimumu diyelim.

Tanımlardan yola çıkarak, aşağıdaki gözlemleri yapmak mümkündür:

1) Supremum/infimum varsa tektir, fakat mutlaka olacak diye bir şart yoktur. Buradan $\mathbb{R}^2$ üzerinde tanımlanmış güzel bir örneğe ulaşabilirsiniz.

2) Bir $A\subseteq \mathbb{R}$ kümesi alttan sınırlı değilse, $\text{inf} A=-\infty$ , üstten sınırlı değilse $\text{sup} A=+\infty$ diyebiliriz. Ayrıca, bu yazımızdakine benzer bir mantıkla, $\text{inf} \hspace{0.1cm} \emptyset = +\infty$ ve $\text{sup} \hspace{0.1cm} \emptyset =- \infty$ olduğunu görebiliriz. Çünkü tanım gereği “ $s\in \emptyset \Rightarrow x\leq s$ ” önermesini doğru kılan her $x\in \mathbb{R}$ elemanının, $\emptyset$ için bir alt sınır olması gerekir.

Diğer taraftan, önermenin ilk kısmı olan “ $s\in \emptyset$ ” ifadesi yanlış (Y) olduğundan, yukarıdaki tablo gereğince, elimizdeki önerme her $x\in \mathbb{R}$ için doğru (D) olacaktır. Yani alt sınırlar kümesi dediğimiz şey aslında tüm $\mathbb{R}$ ‘dir. İnfimum, bu kümenin en büyük elemanı olduğundan, $+\infty$ ‘a eşittir diyebiliriz.
Benzer şekilde, $\mathbb{R}$ ‘nin tüm elemanları $\emptyset$ için bir üst sınır, bunların en küçüğü olarak kabul edilen $-\infty$ ise kümenin supremumudur.

Esas konumuza gelmeden, bir reel sayı dizisinin limit tanımını da hatırlatmakta fayda var. $\{a_n\} \subseteq \mathbb{R}$ bir dizi olmak üzere, $\lim a_n=L$ olması için gerek ve yeter koşul, her $\epsilon > 0$ için, $n\geq N$ olduğunda $|a_n-L|<\epsilon$ olacak şekilde bir $N$ doğal sayısı bulabilmektir. Yani? Bunu bir oyun gibi düşünebilirsiniz. Karşınızdaki kişi size (tercihen oldukça küçük) bir $\epsilon > 0$ sayısı veriyor. Sizden istediği ise, bir $N$ doğal sayısı. Fakat bu, sıradan bir doğal sayı değil. Öyle bir $N$ ki, dizinin bu $N.$ teriminden sonraki tüm terimleri $L$ ‘nin çekim alanından kurtulamamalı, yani, $(a_n-\epsilon, a_n+\epsilon)$ aralığında ikamet etmeli. İşte size verilen her $\epsilon > 0$ sayısına verilebilecek bir yanıtınız varsa, dizinin limitinin $L$ olduğu sonucuna ulaşabilirsiniz. Diğer bir deyişle, sonlu sayıda terimi göz ardı ederek, dizinin sonsuz sayıda teriminin belli bir amaca ulaşmak üzere olduğunu görüyorsak, varış noktamız dizinin limitidir.

Her dizinin bir limiti olmak zorunda değildir. Örneğin $\{(-1)^n\}=(-1, 1, -1, 1, \ldots)$ dizisini ele alalım. Dizimiz -1 ve 1 değerleri arasında ileri geri salınım yapıyor ve belli bir $L$ sayısının çevresinde öbeklenmiyor. Tanımdan yola çıkarak, olası iki adayın, yani -1 ve 1’in, neden dizinin limiti olamayacağını şöyle görebiliriz. Karşı taraf $\epsilon =1$ seçtiğinde, $a_{N}$ sonrasındaki tüm terimler için $|(-1)^n-(-1)|<1$ olacak şekilde bir $N$ bulamayız. ( $(-1)^n=1$ olduğunda işler bozuluyor.) Bu nedenle limit -1 olamaz. Benzer şekilde, $a_{N}$ sonrasındaki tüm terimler için $|(-1)^n-1|<1$ olacak şekilde bir $N$ de bulamayız. (Bu kez $(-1)^n=-1$ olması işi bozuyor.) Demek ki, limit 1 de olamaz.

Görüldüğü gibi, bir limite sahip olmak, bir dizi için öyle kolay iş değil. Yukarıdaki örnekte görüldüğü gibi, sınırlı olmak (yani, her $n\in \mathbb{N}$ için $|a_n|\leq M$ olacak şekilde bir $M$ sayısının olması) bile yeterli olmuyor. Fakat bu noktada, önce Bernard Bolzano, yaklaşık bir 50 yıl sonrasında ise Karl Weierstrass tarafından ispatlanan şu önemli teorem devreye giriyor. $\mathbb{R}^n$ ‘de her sınırlı dizinin, yakınsak bir alt dizisi vardır. Eğer bu yakınsak alt dizilerin sayısı oldukça fazlaysa, elimizde ne işe yarayacağını bilmediğimiz bir sürü limitle baş başa kalıyoruz. İşte tam o an, dağlara taşlara, kurtlara kuşlara isim vermeye aşırı takıntılı bir tür olarak, “bunların en küçüğüne ve en büyüğüne bir isim versek dünya nasıl da güzelleşir” diye düşünmekten kendimizi alamıyoruz. İşte limit superior dediğimiz şey bu alt dizilerin limitlerinin en büyüğü iken, limit inferior en küçüğüdür.

Buradan yola çıkarak, $a_n=(-1)^n$ dizisi için $\lim \text{sup} a_n=1$ ve $\lim \text{inf} a_n=-1$ olduğu sonucuna ulaşabiliriz. Çünkü bu dizi, içerisinde $(a_{n_k})=(1,1,1,\ldots)$ ve $(a_{n_k})=(-1,-1,-1,\ldots)$ yakınsak alt dizilerini barındırır. Bu dizilerin limitleri ise, sırasıyla, 1 ve -1’dir. Diğer bir örnek olarak $a_n=\big (1+(-1)^n+ \frac{1}{2^n} \big)^\frac{1}{n}$ dizisini ele alalım. Bu dizi içerisinde 2 yakınsak alt dizi barındırır: $a_{n_k}=\frac{1}{2}$ ( $n$ tek ise) ve $a_{n_k}=(2+\frac{1}{2^n})^\frac{1}{n}$ ( $n$ çift ise). Bu dizilerin limitleri ise, sırasıyla, $\frac{1}{2}$ ve 1’dir. O halde $\lim \text{sup} a_n=1$ ve $\lim \text{inf} a_n=-1$ olarak bulunur.

Şimdi gelelim işin teknik kısmına. $\{a_n\}$ sınırlı bir dizi olmak üzere,

olduğunu biliyoruz diyelim. İyi güzel de bundan ne anlıyoruz? Bunun için problemi biraz daha somut hale getirelim ve $(a_n)=(2-\frac{1}{2}, 4+\frac{1}{3}, 2-\frac{1}{4}, 4+\frac{1}{5}, 2-\frac{1}{6}, 4+\frac{1}{7}, 2-\frac{1}{8}, 4+\frac{1}{9}, \ldots)$ dizisini ele alalım. Öncelikle $\lim \text{inf} a_n$ ‘i bulmaya çalışalım.

$k=1$ için $\text{inf} \{a_n : n\geq 1\}=\text{inf} \{2-\frac{1}{2}, 4+\frac{1}{3}, 2-\frac{1}{4}, 4+\frac{1}{5}, 2-\frac{1}{6}, \ldots \}= 2-\frac{1}{2}$ ‘dir.

$k=2$ için, $\text{inf} \{a_n : n\geq 2\}=\text{inf} \{4+\frac{1}{3}, 2-\frac{1}{4}, 4+\frac{1}{5}, 2-\frac{1}{6}, 4+\frac{1}{7}, \ldots \}= 2-\frac{1}{4}$ ‘dir.

$k=3$ için, $\text{inf} \{a_n : n\geq 3\}=\text{inf} \{2-\frac{1}{4}, 4+\frac{1}{5}, 2-\frac{1}{6}, 4+\frac{1}{7}, 2-\frac{1}{8}, \ldots \}= 2-\frac{1}{6}$ ‘dir.

$\vdots$

Burada infimumların gittikçe büyüdüğüne, 2’ye oldukça yaklaştığına, fakat asla kavuşamadığına dikkat edelim. Buradan yola çıkarak $\lim \text{inf} a_n=2$ olduğu sonucuna varabiliriz. Benzer bir akıl yürütme ile $\lim \text{sup} a_n=4$ olduğunu görmek de mümkündür.

Lim inf ve lim sup, yakınsak diziler için çok da ilgi çekici bir kavram değildir. Çünkü, dizi nereye yakınsıyorsa, tüm alt dizileri de o noktaya yakınsar. Dolayısıyla lim inf, lim sup ve limit değerlerinin tümü eşit olur.

Lim sup’un en bilinen kullanım alanı, serilerin yakınsaklıklarını kontrol etmek için kullandığımız kök (root) testidir. Kalkülüs derslerinde limit kullanarak verilmiş olsa da, limitin varlığı her zaman garanti olmadığından, lim sup hesabı çok daha kullanışlı olacaktır. Diğer taraftan algoritmaların zaman karmaşıklığını ölçmeye yarayan big-O gösteriminde de lim sup kavramına ihtiyacımız vardır. İlgilenenler buradan devam edebilirler.

Sıralı kümeler ve bu kümeler üzerinde oldukça karıştırılan bazı kavramlardan başlayıp yakınsaklıklara, oradan da limit inferior/superior konularına uzanan bu yazının sonunda, en azından kendi açımdan şu yorumu yapabiliyorum: Zor konu yoktur, fazla ön yargı vardır.

KAYNAKLAR
1) https://web.iitd.ac.in/~sreenadh/MTL100/Lecture6.pdf
2) https://math.stackexchange.com/questions/493526/can-someone-clearly-explain-about-the-lim-sup-and-lim-inf
3) https://www.cantorsparadise.com/why-we-use-the-infimum-and-supremum-in-mathematics-32a90ba13c6c
4) https://cs.pwr.edu.pl/cichon/Math/BigO.pdf

Matematikçinin Uzlaşma Rehberi

Posted on 20 Aralık 2022 by esrakorkmaz

Cevapla

“Çalışmalarıma yeniden başlayacak olsaydım, Platon’un tavsiyesine uyar ve matematikle başlardım.” demiş Galileo Galilei. Her türlü zorluğuna rağmen matematik, bir kere dilinden anlamaya başladığınızda sizlere sonsuz bir öğrenme deneyimi sunuyor. Hem hayatın (uygulamalı matematik) hem de hayalin (pür matematik) bu kadar içinde olması, onu bir türlü anlamadığını ve hatta sevmediğini düşünenleri bile ağına düşürebiliyor.

İşte bir topoloji bloğu oluşturma fikriyle yola çıkıp, çoğu zaman oldukça farklı şeylerden bahsediyor olmam bile, pür matematik çalışan biri olarak, “gündelik hayat matematiğinin” cazibesine kapılıyor olmamdan ileri geliyor. Bu konuda aynı hisleri paylaştığım ve çalışmalarına halen Wellesley College, matematik bölümünde devam etmekte olan Oscar E. Fernandez, gündelik hayatımızın içine sinmiş olan matematiği anlattığı iki mükemmel kitap yazmış: “Everyday Calculus (Gündelik Kalkülüs)” ve “The Calculus of Happiness: How a Mathematical Approach to Life Adds Up to Health, Wealth, and Love? (Mutluluğun Hesabı: Hayata Matematiksel Bir Yaklaşım Nasıl Sağlık, Zenginlik ve Aşk Getirir?)

Bizler de şimdi bir süreliğine “Dünyaya matematik merceğinden bakıyorum ve hemen her şeyin ardındaki gizli matematiği fark etmekten kendimi alamıyorum” diyen Fernandez’in gözünden bakacağız dünyaya. Herhangi bir kişiyle, bir konuda ortak bir karar almaya çalıştığınızı düşünün. Diyelim ki aile bütçenize 500 lira kadar, beklenmedik bir para girişi oluyor. (Miktarın paylaşmaya bile değmeyeceği gerçeğini bir kenara bırakalım lütfen.) Siz tutumlu/eli sıkı biri olarak bunu birikiminize katmak istiyorken, eşiniz bir kerede yiyip bitirmeyi tercih ediyor. En güzeli parayı paylaşıp gönlünüzce kullanmak, peki ama nasıl? İlk akla gelen yarıya bölmek olur, ki bu durumun iki tarafı da memnun edeceğinin bir garantisi yok. Peki ikinizin de maksimum faydası ve memnuniyeti ile sonuçlanacak bir yöntem bulmak mümkün müdür?

Ortada böyle bir problem olur da, matematikçiler buna duyarsız kalabilir mi? Goethe, “Dünya hassas kalpler için cehennemdir” derken, benzer bir durumun hassas zihinler için de geçerli olduğunu nasıl göz ardı edebilmiş acaba? İşte bu probleme oldukça adil bir çözüm getiren “hassas zihin”, 1950 yılında, daha 22 yaşında yayınladığı “The Bargaining Problem (Pazarlık Problemi)” isimli makalesiyle “Beautiful Mind” John Nash olmuştur.

Nash, makalesinde “iki bireyin birden fazla şekilde karşılıklı fayda için işbirliği yapma fırsatına sahip olduğu” durumları incelemekte ve “iki bireyin son derece rasyonel olduğunu, her birinin çeşitli şeylere yönelik isteklerini doğru bir şekilde karşılaştırabildiklerini, eşit derecede pazarlık becerisine sahip olduklarını ve her birinin diğerinin zevkleri ve tercihleri hakkında tam bilgiye sahip olduğunu” varsaymaktadır. Şimdi, Nash’in yaklaşımı kullanılarak, herhangi bir konuda ortak karara nasıl varılabileceğini gösteren bir denklemin nasıl elde edilebileceğini adım adım gösterelim.

1) Bilmemiz gereken ilk şey fayda fonksiyonları (utility functions) olacak. Fayda fonksiyonu, karşımıza çıkabilecek tüm durumlardan gerçel sayılara bir eşleme olarak düşünülebilir ve bir oyuncunun, bir dizi mevcut alternatif arasındaki tercih derecesini ölçer. Örneğin ekonomide, ortada farklı senaryoların olduğu ya da bazı olayların gerçekleşme olasılığının olduğu durumlarda insan davranışını açıklamak için fayda fonksiyonları kullanılır. Diyelim ki biraz hava almak için dışarı çıkmak istiyorsunuz. Bundan elde edeceğiniz fayda, havanın durumuna bağlıdır. Yağmur altında mı yürüyeceksiniz, yoksa kavurucu sıcakta mı? Ama aynı zamanda, elde edilecek fayda, bu durumların gerçekleşme olasılığına da bağlı olabilir. Yani, yağmurun yağacak ya da yağmayacak olmasına bakılmaksızın, yağacağını düşünmeniz bile işleri değiştirir. Bu fonksiyonun çıktısı, söz konusu durumlardaki mutluluk seviyenizin ölçüsü olarak yorumlanabilir.
Elimizdeki mevcut senaryoda, 500 liranın $x$ lirasını almanız durumundaki fayda fonksiyonunu $Y(x)$ fonksiyonu ile gösterelim. Diğer taraftan, eşinizin fayda fonksiyonu, (yani paranın $z$ lirasını alması durumunda sağlayacağı faydayı gösteren fonksiyon) $P(z)$ olsun. Şimdi de aşağıdaki varsayımları yapalım:

(i) Mutluluğu 0 ile 10 arasında ölçeklendirelim. Tahmin edeceğiniz gibi, 0 en mutsuz, 10 ise en mutlu olma durumunu göstersin.
(ii) Paranın size düşen payı arttıkça, eşinizden daha fazla mutlu oluyorsunuz.
(iii) Hiç para almayanın mutluluk seviyesi 0 oluyor.
(iv) Paranın tamamını siz alırsanız mutluluk seviyeniz 10 olurken; paranın hepsini aldığında eşinizin mutluluk seviyesi maksimum 8 oluyor.
Bu koşulları sağlayan birçok fonksiyon bulunabilir. Fakat biz kolaylık açısından aşağıdaki doğrusal fonksiyonlarla çalışalım:
$Y(x)= \frac{10x}{500}$ ve $P(z)= \frac{8z}{500}$
(Bu fonksiyonları doğru orantı yoluyla elde ediyoruz. Örneğin $Y(x)$ fonksiyonunu bulurken, “500 lira aldığınızda mutluluk seviyeniz 10 ise, $x$ lira aldığınızda kaç olur” sorusunu cevaplıyoruz aslında.)

2) Bu aşamada x ve z üzerindeki doğal kısıtlamaları yazalım:
(i) $x+z=500$ , (ii) $x\geq 0$ , (iii) $z\geq 0$
(Yani, aldığınız payların toplamı 500 lira olacak ve her biriniz minimum 0 lira alacaksınız.)

3) Şimdi de, herhangi bir anlaşmaya varılamaması durumunda nasıl hissedeceğinizi ölçeklendirelim. Böyle olumsuz bir senaryoda, sizin mutluluk seviyenizin 3, eşinizin mutluluk seviyesinin ise 4 olduğunu varsayalım.

4) Bu aşamada Nash çarpımı (Nash product) tanımına ihtiyacımız olacak. $u(x)$ ve $v(y),$ sırasıyla, 1. ve 2. oyuncunun fayda fonksiyonlarını; $u(d)$ ve $v(d)$ ise, sırasıyla, 1. ve 2. oyuncunun diğer oyuncuyla pazarlık yapmamaya karar vermesi durumunda elde ettiği faydayı göstermek üzere, $(u(x)-u(d)) (v(y)-v(d))$ çarpımına Nash çarpımı denir. İşte ideal paylaşım nasıl olmalıdır sorusunun cevabı, bu çarpımı maksimum yapan $(x,y)$ noktasıdır.
Bizim problemimizde Nash çarpımı $N=(Y(x)-3) (P(z)-4)$ olacaktır. Kalkülüs derslerinden, bir fonksiyonun mutlak maksimum bulma problemini hatırlayalım. Bunun için önce, elimizdeki kısıtlamalardan yararlanarak, fonksiyonumuzun tek değişkenli bir fonksiyon olarak yazalım. $z=500-x$ olduğundan, $N(x)=(\frac{10x}{500}-3)(\frac{8(500-x)}{500}-4)=\frac{(x-150)(500-2x)}{6250}$ olur. Şimdi de $N(x)$ fonksiyonunun türevini alıp, kritik noktalarını (varsa) bulalım. $N^\prime(x)=\frac{800-4x}{6250}=0$ ise $x=200$ olacaktır.
Demek ki, $(x,z)=(200,300)$ noktası, $N$ fonksiyonunu maksimum değerine ulaştırır, ve bu nedenle işi tatlıya bağlayan paylaşım, siz 200 lira alırken, eşinizin 300 lira almasıdır. Bu çözümün size getireceği fayda $Y(x)=4$ , eşinize getireceği fayda ise $P(z)=4.8$ ‘dir. Kulağa güzel gelmiyor belki ama Nash’in çözümü adildir ve herhangi bir kişinin faydasını maksimize etmeye çalışmaz.

Şimdi yukarıdaki tüm varsayımların ötesinde, genel bir formül elde etmeye çalışalım. Karşınızdaki kişiyle, miktarı $T$ olan bir şeyi nasıl bölüşeceğinize karar vermeniz gerektiğini varsayalım. Bu “şey” illaki para vs. olmak zorunda değil. “Hafta sonunu evde mi geçirsek yoksa dışarıda mı” gibi bir ikilemi bile, $T$ ‘yi toplam zaman alarak çözebilirsiniz. Şimdi $M$ sizin, $N$ ise karşınızdakinin mutluluk düzeyini göstersin, ve bunların yukarıdaki gibi, 0 ile 10 arasında ölçeklendirilmiş olduğunu düşünelim. Son olarak, $Y_d$ ve $P_d$ , sırasıyla, sizin ve karşınızdaki kişinin, anlaşmaya varılamaması durumundaki mutluluk seviyeleriniz olsun. Bu durumda en ideal anlaşma; sizin payınızın

$\frac{T}{2} (1+\frac{Y_d}{M}-\frac{P_d}{N})$ ,

karşınızdaki kişinin payının ise;

$\frac{T}{2} (1+\frac{P_d}{N}-\frac{Y_d}{M})$ ,

olmasıdır. Bu fonksiyonlar elde edilirken, yukarıdaki örnekteki yolları izlemek yeterlidir. Tabii ki 500 yerine $T$ , 3 yerine $Y_d$ , 4 yerine ise $P_d$ yazarak. (Merak edenler, 1 numaralı kaynağın Appendix 6 kısmından yararlanabilirler.)
Son olarak bu denklemlerin bazı özel durumlarını inceleyerek, nasıl sonuçlar ürettiğini birlikte görelim.

(i) Eğer her iki kişi de anlaşmazlık durumundan hiç memnun değilse, yani $Y_d=P_d=0$ oluyorsa, ideal çözüm, yarı yarıya paylaşmak olacaktır. Mantıklı değil mi? İkiniz de tartışmadan kaçan, uzlaşmacı kişilerseniz $T$ ‘yi eşit paylaşmak oldukça iyi bir seçenek olacaktır.

(ii) Şimdi de $Y_d=P_d$ ve sıfırdan farklı oldukları durumu ele alalım. Bu durumda, $N>M$ , yani karşınızdakinin maksimum mutluluğu sizinkinden daha büyükse, onun payı sizinkinden daha küçük olacaktır. Demek ki Nash’in çözümü durumu bir şekilde dengeye ulaştırmaya çalışıyor.

(iii) Son olarak, $M = N$ durumunu inceleyelim. Eğer $Y_d > P_d$ ise, yani anlaşmazlık durumu karşınızdakini daha çok mutsuz ediyorsa, sizin payınız daha büyük olacaktır. Bu durumda sistem sizi bir nevi ödüllendiriyor gibi düşünebilirsiniz.

İnsan ilişkilerini bir dinamik sistem olarak ele alıp, sistemi daha mutlu bir dengeye ulaştırmak için matematiği kullanmak, bizleri daha mutlu ilişkilere götüren bir yol olabilir mi? Ne olursa olsun, denemeye değer.

KAYNAKLAR
1) O. Fernandez, The Calculus of Happiness: How a Mathematical Approach to Life Adds Up to Health, Wealth, and Love, Princeton University Press, 2017.
2) A. Muthoo, Bargaining theory with applications, Cambridge University Press, 1999.

Topolojik bir oluşum!

Author Archives: esrakorkmaz

Neden Matematikçi Olunur? Evrenin Kaynak Koduna Yolculuk

Görünmeyen Boyutlar: Matematikte Uzay Kavramının Evrimi

Gözle Görülür Bir Gerçek, Asırlık Bir Bilmece: Jordan Eğri Teoremi

Cebimizdeki Matematik: GPS, Doğrusal Cebir ve Kozmik Denklemler

Bir Fincan Kahveden Mutlak Gerçeklere : İspat Teknikleri Üzerine

Yakınsaklık vs Düzgün Yakınsaklık

“Zihinsel İşkence”lerden Bilimsel Devrimlere: Karmaşık Sayılar ve Sıralanamaz Doğaları Üzerine

Feynman’ın Perspektifinden Matematik: Uzaylar ve Genelleştirmeler

Sıralamalar, Yakınsamalar ve Ötesi: Limit Superior ve Limit Inferior

Matematikçinin Uzlaşma Rehberi