“Zihinsel İşkence”lerden Bilimsel Devrimlere: Karmaşık Sayılar ve Sıralanamaz Doğaları Üzerine

Günümüzde fizikten mühendisliğe, biyolojiden istatistiğe kadar pek çok alanda kendine yer bulan karmaşık sayıları anlatmak için, oldukça eskiye gitmemiz gerekiyor. Hikayemiz MS 10-70 yılları arasında İskenderiye’de başlıyor. Heron, muhtemelen İskenderiye Kütüphanesi’ni de içeren bir kurum olan Museion’da, hem öğretici hem de araştırmacı olarak bulunan ve matematik, mekanik, fizik, pnömatik gibi birçok alanda çalışmalar yapan bir hezarfen/polimat. Fakat biz burada onun, aeolipile adı verilen ilk buhar türbini, tiyatro sahneleri için tasarladığı özel efektler, otomatik kapılar, otomatlar ve hatta ilkel robotlar gibi birçok icadını bir kenara bırakıp, yalnızca karmaşık sayılarla olan tesadüfi karşılaşmasından bahsedeceğiz.

Yukarıda gördüğünüz cisim bir frustum, yani kesik bir piramit. Heron, Stereometria adlı kitabında, kesik bir koninin yüksekliğinin $h=\sqrt{c^2-\frac{(a-b)^2}{2}}$ formülüyle hesaplanabileceğini göstermiştir. Tabii formülünü bazı özel değerlerler vererek de test etmiştir. Yaptığı denemelerden birinde $a=28, b=4, c=15$ değerlerini seçerek $\sqrt{-63}$ sonucunu bulan Heron, bizlere negatif bir sayının karekökünü içeren bir hesaplamanın ilk örneğini vermiştir. Kendisinin bu geometrik imkansızlık karşısında ne hissettiğini bilmesek de, nasıl bir yol izlediğini biliyoruz. İnsanlığın bu tür matematiksel canavarları düşünmesine daha yüzyıllar varken Heron’un yaptığı, sonucu $\sqrt{63}$ olarak kaydetmek olmuştur. Genellikle sınav kağıtlarında karşılaştığımız gayet klasik bir tepki 🙂 MS 486 yılında, Heron’un izinden giden Hintli matematikçi Bhaskara Acharya ise “Negatif bir sayının karekökü yoktur, çünkü negatif bir sayı, hiçbir sayının karesi değildir.” demiştir.

Şimdi de zamanı biraz ileri sarıp, matematik düellolarının meşhur olduğu 16. yy İtalya’sına doğru uzanalım. Matematik düellosu da nedir diyenlerin, konumuzla da alakalı olan şu yazıya bir göz gezdirmelerini tavsiye ederim. 1510 yılı civarında, Scipione del Ferro $x^3+px=q$ ( $p>0, q>0$ ) biçimindeki kübik denklemler için bir çözüm yolu bulur. Bu noktada, kolaylık için, baş katsayısı 1 olan ve $x^2$ ‘li terim bulundurmayan bu tür denklemlere depressed cubic denildiğini de eklemeden geçmeyelim. Depressed cubic’lerle baş etmeyi öğrenen Del Ferro, bunu asla yayınlamamış, belki de zamanın ruhuna uygun olarak, bir düelloda kullanmak üzere saklamıştır. Del Ferro’nun bu tür denklemleri çözebildiğini biliyoruz, çünkü bu tekniği, hocasının ölümünden sonra depressed cubic’leri çözebilmesiyle övünen öğrencisi Antonio Maria del Fiore’ye öğretmiştir. Bu çözümleri kullanarak ün kazanmak isteyen Fiore, yine bu denklemler üzerinde çalışan Tartaglia’ya, çözmesi için $x^3+3x^2=5$ ve $x^3+6x^2+8x=1000$ denklemlerini göndermiştir. (Gönderilen soruların aslında, “küpü, karesinin 3 katına eklendiğinde 5 olan sayıyı bulunuz” ve “İkincisi birincisinden 2 fazla olan, üçüncü ise ikincisinden 2 fazla olan ve çarpımları 1000 olan üç sayı bulunuz” olduğuna dikkat edelim.)
Fransızlar yaşadığı şehir olan Brescia’yı yağmaladığında, çenesini ve damağını yaran şiddetli bir kılıç yarası aldıktan sonra, konuşması sebebiyle aldığı Tartaglia, yani “kekeme” lakabıyla anılan Niccolò Fontana, kendi kendini yetiştirmiş ve sürekli olarak entelektüel kimliğini kanıtlamaya çalışan bir matematikçidir. Tartaglia, $x^3+px^2=q$ biçimindeki kübik denklemler için bir çözüm yolu bulur ve Fiore’nin meydan okumasına başarıyla karşılık verir. Bu duruma öfkelenen Fiore, Tartaglia’yı 30 soruluk bir düelloya davet eder. Tartaglia Fiore’ye birbirinden farklı problemler gönderirken, sadece hocasının mirası üzerine yükselmeyi amaçlayan Fiore ise, Tartaglia’ya 30 adet depressed cubic gönderir. Tam bir strateji hatası… Bunun üzerine, depressed cubic’ler için bir çözüm yolu bulan Tartaglia, tabii ki bu düellonun kazananı olur. Bu arada Fiore, Tartaglia’nın gönderdiği hiçbir problemi çözemez.

Tartaglia ve Fiore arasındaki matematiksel atışmanın haberi, Milano’daki Gerolamo Cardano’ya ulaşır. Muhtemelen bazılarınıza çok daha tanıdık gelecek olan Cardano, Tartaglia’ya göre daha iyi koşullara doğmuş ve fizik, kimya, astronomi, biyoloji ve matematik gibi birçok alanda çalışmış bir polimat ve bir tıp doktorudur. Otobiyografisinde anlattığı şekliyle “anı yaşayan, açık sözlü, dini küçümseyen, kıskanç, melankolik, bir casus, emanete ihanet eden, bir şeytan, bir tılsım büyücüsü, nefret dolu, iki yüzlü, sahtekar, iftiracı, ve doğası gereği uyumsuz” biri olan Cardano da kübik denklemleri çözmek üzerine girişimlerde bulunur fakat başarısız olur. Bunun üzerine, sırrını öğrenmek umuduyla Tartaglia’yı kendisini ziyaret etmeye davet eder ve
“Kutsal İncil ve bir centilmen olarak inancım üzerine yemin ederim ki, keşiflerinizi bana anlatırsanız asla yayınlamayacağıma ve gerçek bir Hıristiyan olarak, ölümümden sonra kimsenin anlayamayacağı şekilde şifreli olarak yazacağıma söz veriyorum.”
diyerek gizlilik yemini eder. Bunun üzerine Tartaglia, çözümünü bir şiir yoluyla Cardano’ya iletir.

Cardano ayrıca, $x^3+ax^2+bx+c=0$ denkleminde $x=y-\frac{a}{3}$ değişken değiştirmesi yaparak, bu denklemi bir depressed cubic formuna getirmiş ve böylece genel anlamda bir kübik denklemin nasıl çözüleceğini de bulmuştur. Tartaglia’ya verdiği sözü tutmayıp, bu çözümlere Ars Magna (Büyük Sanat) isimli kitabında yer verdiğinde, hem Fiore hem de Tartaglia’yı geride bırakarak, ismini tarihe “kübik denklemleri çözen kişi” olarak yazdırmış olur. Cardano, kitabının 37. bölümünde negatif kökler konusuna yer vererek, bugün karmaşık ya da hayali sayılar olarak adlandırdığımız şeylerin varlığının farkına varan ilk kişi olmuştur. Toplamı 10, çarpımı 40 olan iki sayı ararken, $5+\sqrt{-15}$ ve $5-\sqrt{-15}$ çözümüne ulaşan Cardano’nun, bu sayıların hiçbir yorumu olmadığını, fakat aritmetiğin böyle ilerlediğini not ederek, bu anlamsızlığı görmezden gelmemesi takdir edilesidir. Yine de bu fikri rahatsız edici ya da zihinsel olarak zorlayıcı bulmuş olan Cardano, yapılan işi “zihinsel işkence (mental torture)” olarak nitelendirmiştir.

Tüm bu olanların ardından, 1572 yılında yayınmış olduğu Algebra (Cebir) isimli kitabında Rafael Bombelli, karmaşık sayıları önemsemekle kalmamış, aynı zamanda bu sayılar üzerine aritmetik kurallar da koymuştur. Kendisi bu yüzden karmaşık sayıların mucidi olarak kabul edilir. Bombelli, Cardano’nun formülünü kullanarak $x^3=15x+4$ denklemini çözerken karşılaştığı $+\sqrt{-1}$ sayısını piu di meno, $-\sqrt{-1}$ sayısını ise meno di meno olarak adlandırmış ve bunları kullanarak $(-\sqrt{-1}-1)^3=2-2\sqrt{-1}$ gibi bazı işlemler yapmıştır. Burada, alakasız görünse de, modern cebirsel gösterimin babası François Viète’yi de anmadan geçmeyelim. Çünkü o olmasaydı, belki de matematiği Bombelli gibi yapmaya devam edecektik:

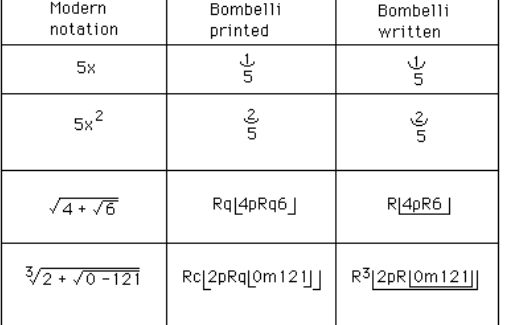
Meraklısı için şu makale Bombelli’nin diline tercüman olabilir.
Son olarak, bugün kullandığımız $i=\sqrt{-1}$ sembolünü ve matematiğin en güzel formülü olarak bilinen $e^{i\pi}+1=0$ eşitliğini literatüre kazandıran Euler’i ve $i=\sqrt{-1}$ sayısını hayali sayı olarak adlandıran Descartes’i anıp, asıl meselemizi tartışmaya başlayalım. Temel problemimiz şu: Acaba karmaşık sayıları da, reel sayıları ya da rasyonel sayıları sıraladığımız gibi sıralayabilir miyiz? Yani iki karmaşık sayı aldığımızda, bunları kıyaslayabilmemize, birinin diğerinden daha küçük/büyük olduğunu söylememize imkan sağlayan bir kural elde edebilir miyiz?

Bunun için önce birkaç deneme yapalım:
1) $a\leq c$ veya $b\leq d$ ise $a+bi\leq c+di$ şeklinde bir sıralama tanımlayalım. Bu durumda $2\leq 8$ olduğundan $2+5i \leq 8-i$ ve $-1\leq 3$ olduğundan $8-i \leq 1+3i$ olduğunu söyleyebiliriz. Sıralamalar hakkında pek de bir şey bilmiyor olsanız bile, $2+5i \leq 8-i \leq 1+3i$ olduğundan $2+5i \leq 1+3i$ eşitsizliğinin sağlanmasını beklersiniz. Fakat ne $2\leq 1$ ne de $5\leq 3$ olduğundan, bu durum doğru değildir.

2) Peki, $a+b\leq c+d$ ise $a+bi\leq c+di$ olarak tanımlasak nasıl olur?🤔 Bu tanımla, hem $2+5i \leq 8-i$ hem de $8-i \leq 2+5i$ oluyor ve bu da pek mantıklı görünmüyor. Çünkü böyle bir durumda $2+5i = 8-i$ olması beklenir.

3) $a\leq c$ ve $b\leq d$ ise $a+bi\leq c+di$ şeklinde bir tanım yapmak daha mantıklı olacak gibi. Çünkü bu şekilde hem sanal hem de reel kısımda işler yolunda gidiyor. Fakat ne yazık ki bu kez, $2+5i$ ve $8-i$ sayılarını karşılaştırmak mümkün olmuyor. Dikkat ederseniz hem $2+5i \leq 8-i$ hem de $8-i \leq 2+5i$ ifadeleri yanlış oluyor.

4) Acaba oldukça geniş bir kullanım alanı olan sözlük sıralaması (lexicographic order) burada da kurtarıcımız olabilir mi? Önce onu bir hatırlayalım: $a<c$ ya da $a=c$ ve $b\leq d$ ise $a+bi\leq c+di$ . Burada $2+5i\leq 8-i$ ve $0\leq 1-2i$ olduğundan, ilk eşitsizliği $1-2i$ ile taraf tarafa çarptığımızda $(2+5i)(1-2i)\leq (8-i)(1-2i)$ , yani $12+i\leq 6-17i$ olmasını bekleriz, fakat maalesef tanımımıza göre bu doğru olmaz.

Denemelerimiz başarısız olduğuna göre, artık kötü düşünmenin zamanı gelmiş demektir. Acaba böyle bir sıralama tanımlamak için boşa kürek çekiyor olabilir miyiz? Bu meseleye geleceğiz, fakat öncesinde bir sıralamadan neler beklediğimizi bir kesinleştirelim. Bunun için keyfi bir X kümesi üzerinde tanımlanan bir sıralamanın
(1) Her $a\in X$ için $a\leq a$ ,
(2) $a\leq b$ ve $b\leq c$ ise $a\leq c$ ,
(3) $a\leq b$ ve $b\leq a$ ise $a=b$ ,
(4) Her $a,b\in X$ için $a\leq b$ ya da $b\leq a$ ,
(5) $a\leq b$ ise $a+c\leq b+c$ ,
(6) $a\leq b$ ve $0\leq c$ ise $ac\leq bc$
koşullarını sağlaması gerektiğini ifade edelim. İspat için çelişkiye varma yöntemi kullanalım. Yani tersine, karmaşık sayılar üzerinde (1)-(6) özelliklerine sahip bir $\leq$ sıralamasının tanımlanabileceğini varsayalım ve bakalım, bu varsayım başımıza ne gibi sorunlar açacak. İspata başlamadan önce, iki küçük Lemma’ya yani yardımcı teoreme ihtiyacımız olacak.
Lemma (a) Her $z$ karmaşık sayısı için $0\leq z \Leftrightarrow -z\leq 0$ gerektirmesi sağlanır.
Kanıt: Öncelikle bunu zaten biliyoruz diye düşünmeyelim. Çünkü elimizdeki $\leq$ sıralaması, reel sayılar üzerindeki klasik büyük/küçük sıralaması değil, karmaşık sayılar üzerinde kurulmuş bambaşka bir sıralama. Bildiğimiz tek şey, bu sıralamanın (1)-(6) özelliklerini sağladığı. Burada, $\leq$ yerine $\prec, \ll, \sqsubset$ gibi bambaşka semboller de kullanabilirdik ama daha standart bir görünüm için klasik bir sembol tercih ettik.
Şimdi ilk olarak, $0\leq z$ olsun. Bu durumda, eşitsizliğin her iki tarafına $-z$ eklersek, (5) numaralı özellikten $-z\leq 0$ elde ederiz. İspatın diğer yönü de benzer şekilde yapılabilir.
Lemma (b) Her $z$ karmaşık sayısı için $0\leq z^2$ dir.
Kanıt: Burada (4) ve (6) numaralı özellikler kullanılarak ispatı tamamlamak mümkündür.

Şimdi asıl ispatı yapmaya hazırız. Öncelikle Lemma (b)’de $z=1$ alırsak, $0\leq 1$ elde ederiz. (Burada, elimizdeki $\leq$ sıralamasının reel sayılar üzerindeki klasik sıralama olmadığını ve bu nedenle $0\leq 1$ eşitsizliğinin zaten sağlandığını düşünmenin yanlış olduğunu bir kez daha vurgulamak isterim.) Bu durumda Lemma (a)’yı uygulayarak $-1\leq 0$ olduğunu da söyleyebiliriz. Bunu bir kenara yazalım. Şimdi Lemma (b)’de $z=i$ alırsak, $0\leq i^2$ yani $0\leq -1$ elde ederiz.
Geldiğimiz noktada elimizde $-1\leq 0$ ve $0\leq -1$ var. Bu nedenle sıralamamızın sağlaması gereken (3) numaralı özellikten $-1=0$ çelişkisini elde ederiz. Demek ki yola çıkış noktamız doğru değil ve bu nedenle karmaşık sayılar üzerinde klasik anlamda bir sıralama tanımlamak mümkün olamaz.