Yeni bir kavramla karşılaştığımda, yapmadan duramadığım bir şey var. Onu ilk kim ortaya atmış, atmasaymış biz bugün nelerden mahrum kalırmışız öğrenmeden edemiyorum. Bir mesai harcayacaksak, kendisini tanımam, kimin nesiymiş bilmem gerekiyor sonuçta. Bu çoğu zaman şu sebepten de olabiliyor. Öğrenim hayatım boyunca, “bunu asla öğrenmeyeceğim, sınavda da çıksa umrumda değil” diye inatlaştığım bazı konular vardı. Geri dönüp baktığımda, böyle olumsuz hislerle dolu olduğum konularda, “bu işin sorumlusu kim” dürtüsüyle daha da merakla doluyorum. İşte “Limit Inferior (lim inf)” ve “Limit Superior (lim sup)” da amigdalama adeta bir sakız gibi yapışmış korkuların başında geliyor.
Uzun zaman sonra yine aklıma düşen bu konuda, dostum ChatGPT’nin de ağzını arıyorum: “Sence Lim inf ve Lim sup karışık konular mı?”, “Olmasalardı ne olurdu”, “1. ya da 2. sınıf bir matematik öğrencisi için biraz ağır konular mı?” minvalinde sorularla manipüle etmeye çalışıyorum onu. Tabii asla geri adım atmıyor ve yine kaçak oynuyor. Kendisi bir dil modeliymiş de, kişisel düşünceleri yokmuş da… Fakat bu konuya kendimizi daha çok maruz bırakırsak, karmaşıklığı ortadan kalkarmış. O halde şimdi birlikte, sıralamaların (order) dünyasından dizilere, ve oradan da Lim inf/Lim sup konularına uzanan bir yolculuğa çıkalım.
İlk olarak oldukça kafa karıştırıcı olan “maksimal, minimal, maksimum, minimum, supremum ve infimum kavramlarını anlamaya çalışalım. Bunun için önce kısmı sıralı (partially ordered) bir kümesi alalım. Kısmi sıralı kümelerde (poset), tam sıralı kümelerden (toset) farklı olarak, kümedeki her iki elemanın birbiriyle kıyaslanmak zorunda olmadığını biliyoruz. Örneğin , dünyadaki tüm insanların kümesi olsun. üzerinde “ ya da ‘nin atasıdır.” bağıntısını tanımlayalım. Bu bir kısmi sıralama bağıntısıdır. Fakat seçtiğimiz 2 kişiden birinin diğerinin atası olması gerekmediği için, bir tam sıralama bağıntısı değildir.
Maksimal vs maksimum eleman: Eğer özelliğini sağlayan her için oluyorsa, ‘ ye maksimal eleman denir. Eğer bir maksimal elemansanız, sizden büyük kimsenin olmadığına eminsiniz. Ama kısmi sıralamanın doğası gereği, kıyaslanamadığınız bazı elemanlar olabilir. Yani herkesten büyük olduğunuzu iddia edemezsiniz. İşte bu noktada maksimum eleman devreye girer. Eğer her için oluyorsa, ‘ye maksimum eleman denir. Maksimum elemansanız, sizden büyük kimsenin olmamasının yanı sıra, küme içindeki her elemandan büyüksünüzdür. Maksimal olmak, bir binanın en üst katında oturmaksa, maksimum olmak, şehirde sizden daha yukarıda yaşayan kimsenin olmamasıdır.
Minimal vs minimum eleman: Yukarıdakine benzer bir ilişki burada da var. Eğer özelliğini sağlayan her için oluyorsa, ‘ ye minimal eleman denir. Yani, diyelim ki, bir minimal eleman ve siz olacak şekilde bir elemanı bulduğunuzu iddia ediyorsunuz. ifadesinin içinde iki ihtimal olduğunu biliyoruz: veya . İşte tanım gereği, ikinci ihtimal asla geçerli olamaz ve böylece olur. Diğer taraftan, minimum eleman, küme içerisindeki her elemanla boy ölçüşme şansı elde etmiş ve bunun sonunda kümedeki her elamandan küçük olarak bulunmuştur. Yani eğer her için oluyorsa, ‘ye minimum eleman denir.
Şimdi bir örnek yapalım: kümesi üzerinde “” kısmi sıralama bağıntısını tanımlayalım. Bu bağıntıya göre 60 ve 90 birer maksimal elemandır. Çünkü eğer ise, yani 60, sayısını bölüyorsa, olmaktan başka şansı yoktur. Benzer bir akıl yürütmeyi 90 için de yapmak mümkündür. Dikkat edersek, bu kümenin, bu bağıntıya göre bir maksimum elemanı yoktur. Eğer 90’dan şüpheleniyorsanız yanılıyorsunuz, çünkü 60, 90’ı bölmediği için diyemeyiz. Yani 90, bu bağıntıya göre, küme içesindeki her elemandan büyük değildir. Benzer şekilde, minimal elamanların 2, 3 ve 5 olduğunu, fakat kümenin bir minimum elemanı olmadığını söyleyebiliriz.
Bu örnekten ve tanımlardan yola çıkarak aşağıdaki gözlemleri yapmak mümkündür:
(1) Kısmi sıralı bir kümede birden çok maksimal eleman olabilir. Ama maksimum eleman varsa, tektir. Kümenin mutlaka bir maksimum/maksimal elemanı olacak diye bir zorunluluk da yoktur.
(2) Her maksimum eleman aynı zamanda bir maksimal elemandır. Fakat, örnekte de görüldüğü gibi tersi doğru değildir.
(3) Eğer kümesi tam sıralı bir küme ise, yani her iki eleman birbiri ile kıyaslanabiliyorsa, her maksimal eleman bir maksimum elemandır. Maksimal elemanı, maksimum olmaktan alıkoyan tek bir engel vardı, o da tüm elemanlara karşı büyüklüğünü ispatlayamama durumuydu. Fakat tam sıralı bir kümede hem her elemanla kıyaslandı, hem de tanımı gereği kendisinden daha büyük bir eleman bulunamadı.
(4) Maksimal/maksimum ya da minimal/minimum eleman olma seçimlerine adaylığımızı koyabilmemiz için, küme içinde ikamet ediyor olma koşulumuz vardır. Yani küme içinde olmayan bir eleman, koşulu sağlasa bile maksimal/maksimum ya da minimal/minimum olarak seçilemez. Bu sorunu biraz sonra, supremum ve infimum tanımı ile çözeceğiz, merak etmeyin 🙂
Üst sınır/ Supremum: Yine bir kısmi sıralı kümemiz ve onun bir alt kümesi olsun. Eğer, her için olacak bir varsa, ‘e, ‘nin bir üst sınırı denir. Dikkat edin, ‘nin üst sınırı kümenin içinde olmak zorunda değil. Bu eleman ya da elemanlar, kümeyi kapsayan, yani bağıntının kaynağı olan kümede de olabilir. Örneğin , alalım. (Burada reel sayıları, bilinen sıralaması ile düşünüyoruz). 1, 2, , sayılarının her biri, kümesi için bir üst sınırdır. Fakat bu kadar çok eleman bulmak oldukça kafa karıştırıcı bir durum. Onun yerine bunların en küçüğüne, yani en küçük üst sınıra, özel bir anlam biçelim ve onu supremum olarak adlandıralım. Bu örnekte , ‘nin supremumu olacaktır. kümesinin bir maksimum elemanı yoktu. Çünkü elamanı kümede yaşamadığı için aday bile olamaz. Fakat, dikkat edersek, supremum olma koşulları arasında küme vatandaşı olma şartı yoktur. Bu durumun bize, integral, serinin yakınsaklık yarıçapı, kümeler arası uzaklık ve Legendre dönüşümü gibi bazı özel tanımlamalara olanak sağlama gibi faydaları olacaktır.
Alt sınır/İnfimum: Şimdi de, “elimdeki küme sınırlı gibi görünüyor, fakat sınırı kümenin içinde değil” problemine yapıcı çözümler sunan infimum tanımına bakalım. İşin mantığı aynı. Öncelikle, her için olacak bir varsa, ‘e, ‘nin bir alt sınırı denir. Eğer ve alırsak, içerisinde, koşulunu sağlayan her sayısının, ‘nin bir alt sınırı olduğunu söyleyebiliriz. Bu kez, teklik takıntımıza derman olacak elaman olarak, bunların en küçüğünü seçmenin anlamsız olduğunu fark ediyorsunuzdur sanırım. O halde, ‘nin her alt sınırı için özelliğini sağlayan alt sınırına, ‘nin infimumu diyelim.
Tanımlardan yola çıkarak, aşağıdaki gözlemleri yapmak mümkündür:
1) Supremum/infimum varsa tektir, fakat mutlaka olacak diye bir şart yoktur. Buradan üzerinde tanımlanmış güzel bir örneğe ulaşabilirsiniz.
2) Bir kümesi alttan sınırlı değilse, , üstten sınırlı değilse diyebiliriz. Ayrıca, bu yazımızdakine benzer bir mantıkla, ve olduğunu görebiliriz. Çünkü tanım gereği “” önermesini doğru kılan her elemanının, için bir alt sınır olması gerekir.
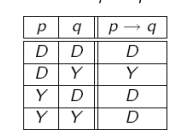
Diğer taraftan, önermenin ilk kısmı olan “” ifadesi yanlış (Y) olduğundan, yukarıdaki tablo gereğince, elimizdeki önerme her için doğru (D) olacaktır. Yani alt sınırlar kümesi dediğimiz şey aslında tüm ‘dir. İnfimum, bu kümenin en büyük elemanı olduğundan, ‘a eşittir diyebiliriz. Benzer şekilde, ‘nin tüm elemanları için bir üst sınır, bunların en küçüğü olarak kabul edilen ise kümenin supremumudur.
Esas konumuza gelmeden, bir reel sayı dizisinin limit tanımını da hatırlatmakta fayda var. bir dizi olmak üzere, olması için gerek ve yeter koşul, her için, olduğunda olacak şekilde bir doğal sayısı bulabilmektir. Yani? Bunu bir oyun gibi düşünebilirsiniz. Karşınızdaki kişi size (tercihen oldukça küçük) bir sayısı veriyor. Sizden istediği ise, bir doğal sayısı. Fakat bu, sıradan bir doğal sayı değil. Öyle bir ki, dizinin bu teriminden sonraki tüm terimleri ‘nin çekim alanından kurtulamamalı, yani, aralığında ikamet etmeli. İşte size verilen her sayısına verilebilecek bir yanıtınız varsa, dizinin limitinin olduğu sonucuna ulaşabilirsiniz. Diğer bir deyişle, sonlu sayıda terimi göz ardı ederek, dizinin sonsuz sayıda teriminin belli bir amaca ulaşmak üzere olduğunu görüyorsak, varış noktamız dizinin limitidir.
Her dizinin bir limiti olmak zorunda değildir. Örneğin dizisini ele alalım. Dizimiz -1 ve 1 değerleri arasında ileri geri salınım yapıyor ve belli bir sayısının çevresinde öbeklenmiyor. Tanımdan yola çıkarak, olası iki adayın, yani -1 ve 1’in, neden dizinin limiti olamayacağını şöyle görebiliriz. Karşı taraf seçtiğinde, sonrasındaki tüm terimler için olacak şekilde bir bulamayız. ( olduğunda işler bozuluyor.) Bu nedenle limit -1 olamaz. Benzer şekilde, sonrasındaki tüm terimler için olacak şekilde bir de bulamayız. (Bu kez olması işi bozuyor.) Demek ki, limit 1 de olamaz.
Görüldüğü gibi, bir limite sahip olmak, bir dizi için öyle kolay iş değil. Yukarıdaki örnekte görüldüğü gibi, sınırlı olmak (yani, her için olacak şekilde bir sayısının olması) bile yeterli olmuyor. Fakat bu noktada, önce Bernard Bolzano, yaklaşık bir 50 yıl sonrasında ise Karl Weierstrass tarafından ispatlanan şu önemli teorem devreye giriyor. ‘de her sınırlı dizinin, yakınsak bir alt dizisi vardır. Eğer bu yakınsak alt dizilerin sayısı oldukça fazlaysa, elimizde ne işe yarayacağını bilmediğimiz bir sürü limitle baş başa kalıyoruz. İşte tam o an, dağlara taşlara, kurtlara kuşlara isim vermeye aşırı takıntılı bir tür olarak, “bunların en küçüğüne ve en büyüğüne bir isim versek dünya nasıl da güzelleşir” diye düşünmekten kendimizi alamıyoruz. İşte limit superior dediğimiz şey bu alt dizilerin limitlerinin en büyüğü iken, limit inferior en küçüğüdür.
Buradan yola çıkarak, dizisi için ve olduğu sonucuna ulaşabiliriz. Çünkü bu dizi, içerisinde ve yakınsak alt dizilerini barındırır. Bu dizilerin limitleri ise, sırasıyla, 1 ve -1’dir. Diğer bir örnek olarak dizisini ele alalım. Bu dizi içerisinde 2 yakınsak alt dizi barındırır: ( tek ise) ve ( çift ise). Bu dizilerin limitleri ise, sırasıyla, ve 1’dir. O halde ve olarak bulunur.
Şimdi gelelim işin teknik kısmına. sınırlı bir dizi olmak üzere,
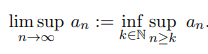
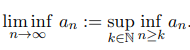
olduğunu biliyoruz diyelim. İyi güzel de bundan ne anlıyoruz? Bunun için problemi biraz daha somut hale getirelim ve dizisini ele alalım. Öncelikle ‘i bulmaya çalışalım.
için ‘dir.
için, ‘dir.
için, ‘dir.
Burada infimumların gittikçe büyüdüğüne, 2’ye oldukça yaklaştığına, fakat asla kavuşamadığına dikkat edelim. Buradan yola çıkarak olduğu sonucuna varabiliriz. Benzer bir akıl yürütme ile olduğunu görmek de mümkündür.
Lim inf ve lim sup, yakınsak diziler için çok da ilgi çekici bir kavram değildir. Çünkü, dizi nereye yakınsıyorsa, tüm alt dizileri de o noktaya yakınsar. Dolayısıyla lim inf, lim sup ve limit değerlerinin tümü eşit olur.
Lim sup’un en bilinen kullanım alanı, serilerin yakınsaklıklarını kontrol etmek için kullandığımız kök (root) testidir. Kalkülüs derslerinde limit kullanarak verilmiş olsa da, limitin varlığı her zaman garanti olmadığından, lim sup hesabı çok daha kullanışlı olacaktır. Diğer taraftan algoritmaların zaman karmaşıklığını ölçmeye yarayan big-O gösteriminde de lim sup kavramına ihtiyacımız vardır. İlgilenenler buradan devam edebilirler.
Sıralı kümeler ve bu kümeler üzerinde oldukça karıştırılan bazı kavramlardan başlayıp yakınsaklıklara, oradan da limit inferior/superior konularına uzanan bu yazının sonunda, en azından kendi açımdan şu yorumu yapabiliyorum: Zor konu yoktur, fazla ön yargı vardır.
Topolojik bir oluşum! 
Geri bildirim: Yakınsaklık vs Düzgün Yakınsaklık | Topolojik bir oluşum!