Sene 1911. Trablusgarp savaşı başlar ve dünya tarihindeki ilk hava saldırısı gerçekleşir. Başına geleceklerden habersiz Titanic, ilk kez denize indirilir. Ulusal anlamda ilk emekçi kadınlar günü düzenlenir. İnsanoğlu Güney Kutbu’na ilk kez başarıyla ulaşır. Tüm bu önemli gelişmeler meydana gelirken, Otto Toeplitz isimli bir Alman matematikçi, yaptığı bir konuşmada, “On some problems in topology (Topolojide bazı problemler)” başlığı altında şu soruyu ortaya atar:
Elimizde iki boyutlu uzayda verilmiş basit kapalı bir eğri (ne menem bir şey olduğundan burada bahsetmiştik) olduğu varsayalım. Acaba bu eğri üzerinde, birleştirildiğinde bir kare oluşturacak şekilde 4 nokta bulmak mümkün müdür?
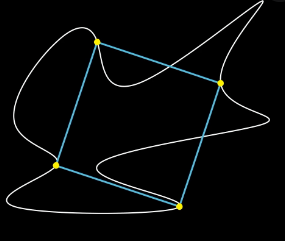
Görünen o ki, Toeplitz bu problemin kanıtı ile ilgili bir makale yayınlamamıştır. Günümüzde bile tam anlamıyla çözülmemiş olan bu meşhur problem, Toeplitz Sanısı (diğer isimleriyle, Inscribed Square Problem ya da Square Peg Problem) olarak bilinmektedir. Yukarıdaki şekilde de görüldüğü üzere, çizilecek karenin tamamıyle eğrinin içinde kalması gerekmiyor.
Eğer elimizdeki eğri bir çember ya da elips ise, böyle bir çemberin mevcut olduğunu görmek gayet kolaydır. Dahası, eğrimiz bir kedi, tavşan ya da filse de işler gayet yolunda gidiyor 🙂
Toeplitz Sanısı parçalı düzgün (piecewise smooth), parçalı analitik veya orijine göre simetrik eğriler gibi bazı özel ve iyi huylu denilebilecek eğriler için ispatlanmıştır. Sanıyı yerel monoton eğriler için ispatlayan Stromquist, mutlak çözüme en çok yaklaşan kişi olmuştur. Stromquist’e göre, eğer bir basit kapalı eğri “yeterince iyi” ise, istenilen karenin çizilmesi mümkün olacaktır. Peki burada eğrinin “yeterince iyi” olması ne demektir? Bunu anlamak için eğri üzerinde keyfi bir P noktası seçelim. Eğer eğrinin, P noktasını içeren bir parçası, bir 
Toeplitz Sanısı hala tam bir ispat bekliyor. 2017 senesinde, yaşayan en büyük matematikçi olarak değerlendirilen Terence Tao, bu asırlık probleme bir el atmıştır. Diğer taraftan, Covid-19 zamanında yaşadığımız karantina dönemini bir fırsata çeviren Joshua Greene and Andrew Lobb, sanının dikdörtgenler üzerine olan bir uyarlamasını ispatlamışlardır.
Dikdörtgenler için olan versiyonu daha iyi anlamak isteyenler, konu hakkında oldukça açıklayıcı bir anlatıma buradan ulaşabilirler.
İfade edildiğinde gayet kolay olduğu düşünülen bazı gerçekleri matematiksel olarak kanıtlayabilmek bazen çok zor ve hatta imkansız olabiliyor. İspat bekleyen tüm bu sanılar, bilim söz konusu olduğunda belki de sadece bir arpa boyu yol gittiğimizi fark etmemizi sağlıyor.
KAYNAKLAR
1) http://diposit.ub.edu/dspace/bitstream/2445/151918/2/151918.pdf
2) https://www.3blue1brown.com/lessons/inscribed-rectangle-problem
3) https://interestingengineering.com/two-mathematicians-crack-age-old-geometry-problem-in-quarantine
4)https://en.wikipedia.org/wiki/Inscribed_square_problem#:~:text=The%20inscribed%20square%20problem%2C%20also,and%20in%20other%20special%20cases.
5) https://www.webpages.uidaho.edu/~markn/squares/
Topolojik bir oluşum! 