Bağlantılılık vs Yol Bağlantılılık: Topolojicinin Sinüs Eğrisi

Kompaktlık ve bağlantılılık topolojininin en önemli iki özelliğidir. Kompaktlık kelimesi, bu özelliğin neye benzediği hakkında pek bilgi vermese de, “bağlantılılık” tam da ismiyle müsemma bir özellik gibi duruyor. Örneğin, bağlantılı bir küme, tek bir parçadan oluşmalı ve içinde alınan her iki noktayı, yine kümenin içinde kalacak bir çizgi ile birleştirmek mümkün olmalıymış gibi geliyor. Çoğu küme için bu durum geçerli olabilir, fakat bazı patolojik kümeler için bu sezgisel yaklaşım pek de çalışmıyor. Örneğin aşağıdaki şekilde gösterilen sonsuz süpürge uzayını (infinite broom) ele alalım. Bu uzay, $(0,0)$ noktasından $(1,\frac{1}{n})$ noktasına giden doğru parçaları ile $(1,0)$ noktasının birleşiminden oluşur. x-ekseni üzerindeki $(0,1)$ aralığı ise kümeye dahil değildir.

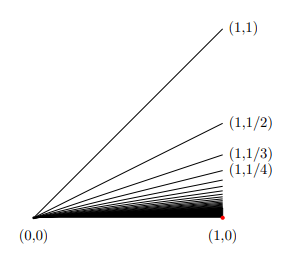
Sonsuz süpürge temel olarak iki parçadan oluşur. Doğru parçaları ve tek başına duran $(1,0)$ noktası. Doğrular üzerinden aldığımız bir noktayı, küme içinde kalmak şartıyla, $(1,0)$ noktasına bağlamak mümkün görünmüyor. Fakat bu uzay topolojik olarak bağlantılı bir uzay. Demek ki, tek parça olma ve her iki noktayı birbirine bağlayabilme, bağlantılı küme tanımı için yeterli değil ve aslında iki farklı bağlantılılık kavramına ihtiyacımız var.

Bunlardan ilki, sezgisel olarak da bulabildiğimiz, “yol bağlantılılık”. Eğer bir $A$ kümesi içerisinde alınan her iki noktayı, yine $A$ ‘nın içinde kalacak bir yol ile birbirine bağlayabiliyorsak, $A$ kümesi yol bağlantılıdır diyeceğiz. Fakat burada yol kavramını matematiksel olarak ifade etmemiz gerekiyor.

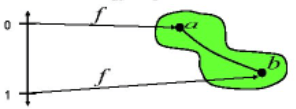
Herhangi iki $a, b\in A$ noktası arasında bir yol ile kastedilen şey, $f:[0,1]\rightarrow A$ , $f(0)=a, f(1)=b$ özelliklerini sağlayan sürekli bir fonksiyondur.

Diğer taraftan bağlantılılık tanımı, alışılagelen tanımlamalardan biraz farklıdır. Çünkü bu kez önce “bağlantısız” olma tanımını yapıp, onun yardımıyla bağlantılılık tanımına gideceğiz.

Eğer uzayımız, boştan farklı, ayrık iki açık kümenin birleşimi olarak yazılabiliyorsa, bu uzay bağlantısızdır diyeceğiz. Bu şekilde bir yazım mümkün değilse de, kümemiz bağlantılı olacak.

Yol bağlantılı her uzay bağlantılıdır. Yani eğer her iki nokta arasında bir bağlantı kurmak mümkünse, kümeyi iki farklı parçaya ayırmak da mümkün olmayacaktır. Fakat tersi her zaman doğru değildir. Örneğin sonsuz süpürgenin yol bağlantılı olmadığı gayet açıktır. Diğer yandan bu küme bağlantılıdır, çünkü $n\rightarrow \infty$ iken, çizilen çubuklar $(1,0)$ noktası etrafında öyle sıklaşır ki, uzayı boştan farklı, ayrık açıkların birleşimi olarak yazmak mümkün olmaz.

Yol bağlantılı olmayıp bağlantılı olan kümelerin en güzel örneği, tanımı ve grafiği aşağıdaki gibi olan, Topolojicinin Sinüs Eğrisidir.

$S=\{(x,y)\in \mathbb{R}^2 : y=\sin(\frac{1}{x}), x\in (0,1]\}\cup (\{0\}\times [-1,1])$

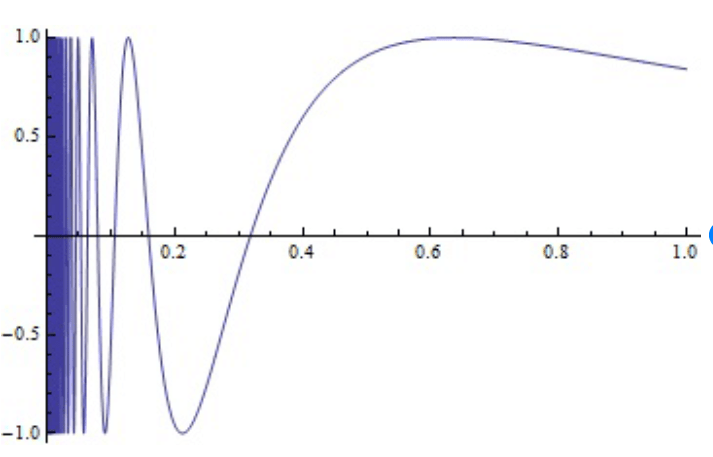
Burada, sezgisel olarak, sonsuz süpürgeye benzer bir durum söz konusu. Yani salınımlar y-ekseni üzerindeki $[-1,1]$ aralığında oldukça sıklaşıyor. İşte bu nedenle kümeyi parçalamak olası görünmüyor. Diğer taraftan, $f(x)=\sin(\frac{1}{x})$ kısmından alınan bir nokta ile $S_0=\{0\}\times [-1,1]$ doğru parçası üzerinde alınan herhangi iki noktayı bağlayan bir yol bulunamıyor.

Şimdi biz, topoloji kitaplarınının vazgeçilmezi olan ve çoğunlukla kanıtsız verilen, “topolojicinin sinüs eğrisi bağlantılıdır fakat yol bağlantılı değildir” ifadesini ispatlamaya çalışalım.

Öncelikle $S$ kümesini $S_0=\{0\}\times [-1,1]$ ve $S_1=\{(x,y)\in \mathbb{R}^2 : y=\sin(\frac{1}{x}), x\in (0,1]\}$ olmak üzere iki parçaya ayıralım. Burada $f(x)=\sin(\frac{1}{x})$ olmak üzere, $S_1=f((0,1])$ olduğu açıktır.

(1) Bağlantılı bir uzayın sürekli bir fonksiyon altındaki görüntüsü de bağlantılıdır.

O halde, $f$ fonksiyonu $(0,1]$ aralığında sürekli ve $(0,1]$ aralığı bağlantılı olduğundan, $S_1$ kümesinin de bağlantılı oluğunu açıktır.

(2) Bağlantılı bir kümenin kapanışı da bağlantılıdır.

Demek ki $S=\overline {S_1}$ olduğunu gösterebilirsek, $S$ ‘nin bağlantılı olduğu sonucuna ulaşabiliriz.

İlk olarak $S\subseteq \overline {S_1}$ kapsaması için bir $p\in S=S_0\cup S_1$ alalım.

(3) $(X,d)$ bir metrik uzay, $x\in X$ ve $A\subseteq X$ olsun. Bu durumda, $x\in \overline{A}$ olması için gerek ve yeter koşul, $x_n \rightarrow x$ olacak şekilde bir $\{x_n\}_{n\in \mathbb{N}}\subseteq A$ dizisi olmasıdır.

O halde, $p\in \overline {S_1}$ olduğunu görmek için, $S_1$ kümesinde, $x_n \rightarrow p$ olacak şekilde bir $\{x_n\}_{n\in \mathbb{N}}$ dizisi elde etmeye çalışalım. Eğer $p\in S_1$ oluyorsa $x_n=(p,p,p,\ldots)$ olarak alabiliriz. Ama eğer $p\in S_0$ oluyorsa, diziyi yazmak öyle kolay olmayacak. Öncelikle $p\in S_0$ ise, $p=(0,y)$ ( $|y|\leq 1$ ) biçimindedir. Ayrıca $y=\sin \theta$ olacak şekilde bir $\theta \in [-\pi,\pi]$ vardır, çünkü $g(x)=\sin x$ , görüntü kümesi $[-1,1]$ olan örten bir fonksiyondur. Diğer taraftan, $g(x)=\sin x$ fonksiyonu $2\pi$ periyotlu olduğundan, her $n \in \mathbb{N}$ için $y=\sin(\theta+2n\pi)$ ‘dir. Şimdi, $x_n=\frac{1}{\theta+2n\pi}$ olarak seçersek, her $n$ için $\sin(\frac{1}{x_n})=y$ olur. Hatta, $n\rightarrow \infty$ iken $x_n \rightarrow 0$ olduğundan $(x_n, \sin(\frac{1}{x_n}))=(x_n,y) \rightarrow (0,y)$ elde edilir. Burada herhangi bir $|y|\leq 1$ için, elde ettiğimiz dizi aslında, x-eksenine paralel olan ve bu $y$ noktasından geçen doğrunun, $y=\sin(\frac{1}{x})$ ‘in grafiğini kestiği noktalardan oluşan dizidir.

Şimdi diğer kapsamayı, yani $\overline {S_1} \subseteq S$ olduğunu görmeye çalışalım. Öncelikle kümelerin tanımından $S_1\subseteq S$ olduğu açıktır. Burada eğer $S$ kümesinin kapalı olduğunu kanıtlayabilirsek, $\overline {S_1} \subseteq \overline {S}=S$ olur ve böylece amacımıza ulaşmış oluruz. Bunun için de, (3)‘ü kapalı bir $A$ kümesine uyarlayarak elde edebileceğimiz,

(4) $A$ kümesinin kapalı olması için gerek ve yeter koşul her $\{x_n\}_{n\in \mathbb{N}}\subseteq A$ , $x_n \rightarrow x$ dizisi için $x\in A$ olması (yani $A$ ‘nın, tüm limit noktalarını içermesidir)

teoremini kullanalım.

Bunun için $S$ kümesinde $(x_n,y_n) \rightarrow (x,y)$ olacak şekilde bir $\{(x_n,y_n)\}_{n\in \mathbb{N}}$ dizisi alalım ve $(x,y)\in S$ olduğunu gösterelim. Öncelikle, $x=\lim x_n$ ve $y=\lim y_n$ olduğundan, $x\geq 0$ ve $|y|=\lim|y_n|\leq 1$ özellikleri sağlanır. Eğer $x=0$ ise, $(x,y)=(0,y)$ ve $|y|\leq 1$ olduğundan, $(x,y)\in S$ elde etmiş oluruz. Şimdi ikinci olasılığı yani $x>0$ olma durumunu inceleyelim. Bunun için önce $x$ ‘in yalnızca pozitif sayılardan oluşan bir $\epsilon$ -komşuluğunu alalım. (Burada $\epsilon<|x|$ seçmemiz yeterli olacaktır.) $x_n \rightarrow x$ olduğundan, her $n>N$ için $x_n\in B(x,\epsilon)=(x-\epsilon, x+\epsilon)$ olacak şekilde bir $N$ doğal sayısının varlığından söz etmek mümkündür. Yani demek ki, $x_n$ dizisinin sonlu sayıdaki bazı elemanları hariç olmak üzere, $x_n>0$ varsayımını yapabiliriz. İşte bu sonsuz çoklukta eleman için $(x_n, y_n)\in S_1$ ve böylece $y_n= \sin(\frac{1}{x_n})$ ‘dir. Ayrıca, $f(x)=\sin(\frac{1}{x})$ fonksiyonu $(0,\infty)$ aralığında sürekli olduğundan,

$y=\lim y_n=\lim \sin(\frac{1}{x_n})=\sin(\frac{1}{x})$

sağlanır ve böylece $(x,y)\in S_1\subseteq S$ ‘dir.

Şimdi de, sinüs eğrisinin yol bağlantılı olmadığını gösterelim. Grafikten de anlaşılacağı gibi esas problem, $S_0$ ‘dan alınan bir nokta (örneğin (0,1) noktası) ile $S_1$ ‘den alınan bir nokta arasında bir yol bulunamamasıdır. Tabii bunu usulünce yapmak için, bu şekilde alınan iki noktayı birleştiren bir yol olduğunu kabul edip, bunun bir çelişkiye yol açacağını görmeye çalışalım. O halde, tersine, $h(0)\in S_1$ ve $h(1)=(0,1)\in S_0$ olacak şekilde sürekli bir $h:[0,1]\rightarrow S$ fonksiyonunun olduğunu varsayalım. $h$ sürekli olduğundan, özel olarak $\epsilon=\frac{1}{2}$ için, $1-\delta< t<1$ iken $||h(t)-(0,1)||< \frac{1}{2}$ olacak şekilde bir $\delta>0$ vardır. Burada $[1-\delta,1]$ aralığı bağlantılı olduğundan, (1)‘den $h([1-\delta,1])$ de bağlantılıdır.

$h(1-\delta)=(x_0,y_0)$ olsun. $p_1:\mathbb{R}^2 \rightarrow \mathbb{R}$ , $p_1(x,y)=x$ birinci izdüşüm fonksiyonu olmak üzere, $p_1$ ile $h:[0,1]\rightarrow \mathbb{R}^2$ ‘nin bileşkesini, yani $p_1\circ h$ fonksiyonunu ele alalım. Öncelikle, izdüşüm fonksiyonları sürekli olduğundan, bu bileşke fonksiyonu da süreklidir. Bu nedenle $(p_1\circ h)([1-\delta,1])$ kümesi, $\mathbb{R}$ ‘nin bağlantılı bir alt kümesidir. Ayrıca $(p_1\circ h)(1)=0$ ve $(p_1\circ h)(1-\delta)=x_0$ olduğundan, bu küme 0’ı ve $x_0$ ‘ı içerir.

(5) $A\subseteq \mathbb{R}$ bağlantılı bir alt küme ise, $A$ bir aralıktır.

O halde $(p_1\circ h)([1-\delta,1])$ , yani $h([1-\delta,1])$ ‘deki noktaların x-koordinatlarının kümesi, tüm $[0,x_0]$ aralığını içerir. Böylece $x_1\in (0,x_0]$ için $h(t)=(x_1, \sin(\frac{1}{x_1}))$ olacak şekilde bir $t\in [1-\delta,1]$ vardır.

Şimdi, yeterince büyük bir $n\in \mathbb{N}$ için, özel olarak, $x_1=\dfrac{1}{2n\pi-\frac{\pi}{2}}$ olarak seçelim. Bu durumda $\sin(\frac{1}{x_1})=\sin(-\frac{\pi}{2})=-1$ ve böylece $t\in [1-\delta,1]$ için $h(t)=\big(\dfrac{1}{2n\pi-\frac{\pi}{2}}, -1\big)$ olur. Fakat bu durum, daha önce elde etmiş olduğumuz $||h(t)-(0,1)||< \frac{1}{2}$ koşulu ile çelişir. Çünkü, $||h(t)-(0,1)||=\sqrt{\big(\dfrac{1}{2n\pi-\frac{\pi}{2}}-0 \big)^2+(-1-1)^2}\geq 2$ olmalıdır.