Ütopya Sevenlere: Düzülke

Posted on 24 Şubat 2022 by esrakorkmaz

“Eğer bile bile gücünüz yettiğinden daha azını olmayı planlıyorsanız; sizi uyarırım, hayatınızın geri kalan kısmında mutsuz olacaksınız. Kendi yeteneklerinizden ve olanaklarınızdan kaçıyor olacaksınız.” Abraham Maslow

Beynimiz sadece üç boyuta sıkışmış olsa da, algılarımız bize yeni kapılar açıyor ve daha yüksek boyutların varlığından bile bahsedebiliyoruz. Örneğin Süper Sicim Teorisi evrenin 10 boyutlu olduğunu, M-teorisi ise 11 boyutlu olduğunu öne sürerken; Bozonik Sicim Teorisi 26 boyutun var olduğu fikrini ortaya koyuyor. İşte tüm bunlar bize, insanın sınırları aşma potansiyelini ve hevesini gösteriyor.

Yüksek boyutlardan ve onları nasıl algılayabileceğimizden bahsetmeden önce, boyutun ne olduğuna bir bakalım. Bunun için, elimizdeki matematiksel nesneden (doğru, düzlem, küre vs.) bir nokta alalım ve bu noktayı belirlemek için ihtiyacımız olan minimum koordinat sayısını düşünelim. İşte bu sayı bize, o nesnenin kaç boyutlu olduğunu söyleyecektir. Örneğin, bir düzlem üzerinde alınan bir noktayı ifade etmek için iki, bir küre üzerinde alınan bir noktayı ifade etmek için ise 3-koordinata ihtiyaç vardır.

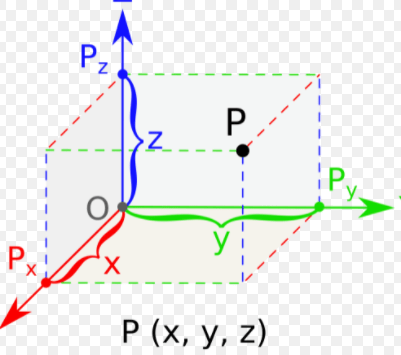
Burada tüm koordinat eksenlerinin birbirine dik olduğuna dikkat edelim. 4-boyutlu bir nesneyi görselleşirmek için 4 adet koordinat eksenine ihtiyaç vardır ve tabii ki bu 4. eksen, diğer üçüne dik olmalıdır. Bunu anlamak pek de mümkün gibi görünmüyor, ama biz en azından, küpün 4-boyutlu bir analoğu olan tesseract‘ın neye benzediğini algılamaya çalışalım.

Tesseract, téssara-aktís yani dört-doğru demektir. Çünkü 3-boyutlu bir nesne olan küpte, her bir köşeden çıkan doğru sayısı üç iken, 4-boyutlu tesseractta bu sayı dörttür. Bir küp nasıl karelerden oluşuyorsa, tesseract da küplerden oluşur ve açıldığında tam olarak şöyle bir şeye benzer:

Tessaract’ın ne kadar popüler olduğunu anlamak için, birçok Marvel filminde yer aldığını ve Yıldızlararası (Interstellar) filmindeki Tesseract sahnesini hatırlamak yeterli olacaktır sanırım.

4. boyuttan bahsetmişken, “zaman” boyutundan bahsetmeden geçmek olmaz. Zaman da bir boyuttur, çünkü bir nesnenin uzaydaki yerini kesin olarak belirleyebilmek için zaman parametresine de ihtiyaç vardır. Bunu anlamak için, bir A noktasından B noktasına hareket ettiğimizi düşünelim. Aynı anda hem A hem de B noktasında olmamız mümkün değildir, yani konumumuz değişirken aslında zaman koordinatında da bir değişiklik yapmış oluruz. Tabii bu boyutta hareket, asla geriye doğru değil, sadece ileriye doğru olacaktır. Burada ilginç olan, uzayda ne kadar hızlı hareket edersek, zamanda o kadar yavaş hareket ettiğimiz, yani az yol katettiğimizdir. Demek ki ışık hızına ulaşabilmiş olsaydık, zaman boyutunda hiç hareket etmemiş olurduk. Uzmanı olmadığım bu konuda daha derine girmeyeceğim. Tüm bu anlattıklarım, zaman ve uzayın birbirinden ayrılamaz olduğunu ve zamanın da bir boyut olarak düşünülmesi gerektiğini görmek içindi.

Dördüncü boyut fikri aslında çok da yeni değildir. Örneğin Henry More 1659 tarihli Ruhun Ölümsüzlüğü (The Immortality of the Soul) isimli kitabında, ruhun dördüncü boyutta olduğundan bahsetmiştir. D’ Alambert 1754, Lagrange ise 1797 yılında dördüncü boyut kavramından dem vurmuşlardır. Zamanın dördüncü boyut olduğu fikrine ise, bilim kurgunun babası olarak bilinen H.G. Wells’in, 1895 yılında yazdığı Zaman Makinası kitabında yer verilmiştir:

“Zaman Gezgini, “Açıkçası,” diye sözünü sürdürdü, “herhangi bir gerçek cismin dört yönde uzantısı olmalıdır: Uzunluğu, Genişliği, Kalınlığı ve Sürekliliği olmalıdır. Ama insan doğasının birazdan açıklayacağım bir zaafı yüzünden görmezden gelmeye yatkınızdır. Aslında dört boyut vardır, bunların üçüne Uzay’ın üç düzlemi diyoruz, dördüncü boyut ise Zaman’dır. Ama ilk üç boyut ile dördüncü boyut arasında gerçekdışı bir ayrım yapma eğilimindeyizdir, bunun nedeni bilincimizin hayatımızın başından sonuna kadar bu dördüncü boyut boyunca kesik kesik ilerliyor olmasıdır.”

Dördüncü boyutu daha iyi kavramak için, önce iki boyutta yaşayanların dünyasını ziyaret edelim ve onların üçüncü boyutu nasıl algıladıklarına bir bakalım. Bunu yaparken başvuracağımız kaynak Edwin Abbott Abbott‘ın, Türkçe’ye Düzülke ismiyle çevrilmiş ve ilk olarak 1884 tarihinde yayınlanmış olan Flatland: A Romance of Many Dimensions kitabı olacak.

İsminden de anlaşılacağı gibi, Düzülke aslında 2-boyutlu bir dünya. Baş kahramanımız Kare, sakinleri düz çizgiler, üçgenler, kareler, beşgenler, altıgenler ve daha başka şekiller olan bir düzlemde yaşıyor. Şimdi kendimizi onun yerine koyalım. Karşıdan gelen bir Düzülke sakinine, örneğin bir beşgene baktığımızda, onu sadece bir çizgiden ibaret olarak görürüz. Bu nedenle bir şekli diğerinden ayırt edebilmek pek de mümkün değildir.

Fakat Düzülke sakinlerinin bunu anlamak için, sesleri ayırt etme gibi bazı yöntemleri vardır. Bu arada kitap sadece boyut kavramını değil, ülkenin iklimi, evleri ve sakinleri gibi konularda da detaylı bilgiler ve gerçekten güzel bir kurgu içeriyor.

Fazla uzatmayalım, onların takvimiyle 1999 yılının son günü, bizim Kare gaipten bir ses duyar. Daha sonra ise önünde, sürekli olarak büyüklüğü değişen bir şekil belirir.

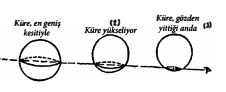
Bazen tek bir nokta, bazense bir çembere benzeyen bu şekil, uzaydan geldiğini söyler ve uzayın aslında 3-boyutlu olduğunu iddia eder. Bir Uzayülke sakini olan bu kürenin olağanüstü güçleri de vardır. Mesela bir Düzülke sakininin kapalı kabul ettiği şeylerin içini görebilir. Kapalı bir kareye yukarıdan bakan biri olarak bunu anlamamız oldukça kolay değil mi? İlk başta Küre’yi bir sahtekar olmakla suçlayan Kare, Uzayülkeyi ziyaret eder ve atası olan Küp de dahil olmak üzere birçok 3-boyutlu cisim ile tanışır:

Ne olduklarını tam olarak algılayamasa da, Uzayülke sakinlerinin varlığına inanan kare, işi biraz daha ileri götürür ve Küre’den, ona dört boyut ülkesinden bahsetmesini ister. Fakat ilginçtir ki, Küre ona, böyle bir şeyi aklın almadığını ve bunun bir saçmalık olduğunu söyler.

Küre’nin saçmalık olarak nitelendirdiği dördüncü boyutu anlamak için, Abbott’un, çağının ötesinde olduğunu düşündüğüm bu kitabını mutlaka okumanızı öneririm. Çünkü Düzülke, üçüncü ve dördüncü boyut arasındaki ilişkinin mükemmel bir analojisidir.

Aslında bizler de, özellikle kalkülüs derslerinde, 3-boyutlu bir nesnenin neye benzediğini anlayabilmek için, o nesneyi, farklı seviyelerde yaşayan Düzülke sakinlerinin gözünden görmeye çalışıyoruz. Bunun için, $z=f(x,y)$ fonksiyonuyla verilen nesnemizi, $z=c$ düzlemleriyle kesiyoruz ve her bir kesişimde elde ettiğimiz şekle, bir seviye eğrisi (level curve) diyoruz. (Tabii nesneyi daha iyi tanımak için, aynı zamanda $x=c$ ve $y=c$ düzlemleri ile kesmeyi de ihmal etmiyoruz.) Sonuç olarak 3-boyutlu cismimiz, tüm bu kesişim eğrilerinin üst üste konmasıyla oluşan bir cisim oluyor.

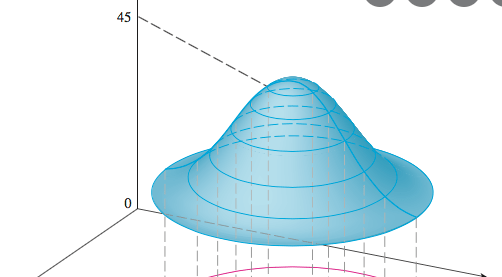
Benzer şekilde, $w=f(x,y,z)$ ile verilen 4-boyutlu bir nesneyi anlamak için, bu cismi $w=c$ ‘lerle keserek, $c=f(x,y,z)$ yüzeylerini elde ediyor ve elde ettiğimiz şekillere birer seviye yüzeyi (level surface) diyoruz.

Boyut konusu, bu kadar az bilgiyle sınırlandırılamayacak kadar geniş ve zihnimizi alt üst edecek kadar karışık. Fakat yine de daha fazla şey görmek/öğrenmek isteyenler için aşağıdaki videolar iyi bir başlangıç olacaktır.
https://www.youtube.com/watch?v=Q_B5GpsbSQw

https://www.youtube.com/watch?v=YMuc3m4wnZE

KAYNAKLAR
1) F. Cajori, Origins of Fourth Dimension Concepts, The American Mathematical Monthly 33(8), 397-406,1926.
2) Edwin Abbott Abbott, Düzülke, Alfa Yayınları, 2015.
3) https://en.wikipedia.org/wiki/Tesseract
4) https://plato.stanford.edu/entries/henry-more/

Explained: Arşimet (Archimedean) Özelliği

Posted on 11 Şubat 2022 by esrakorkmaz

Matematikte, kendisinden uzun uzun bahsedilmeyen, ne işe yaradığı çok da bilinmeyen, fakat aslında kanıksadığımız birçok gerçeğin nedenini anlamamıza yardımcı olan, ve hatta çoğu ispatta alttan alta kullanılan bazı temel özellikler vardır. İşte şimdi, bu özelliklerden biri olan Arşimet (Archimedean) özelliğinden bahsedeceğiz. Küçük bir uyarı: Anlatacağım özelliğin meşhur “Eureka Anı” ile hiçbir ilgisi yok. Avusturyalı matematikçi Otto Stolz’un bu özelliğe “Arşimet özelliği” demesinin sebebi, orijinal halinin, Arşimet’in Küre ve Silindir Üzerine isimli çalışmasında V. aksiyom olarak bulunması.

Aksiyomun orijinal ve günümüzdeki ifadesinden bahsetmeden önce geniş bir terminolojiye ihtiyacımız olacak. O halde işin en temeline inelim ve işe, sıralı cisimlerin tanımı ile başlayalım.

Bir $S$ kümesi üzerinde bir sıralama (order), aşağıdaki özellikleri sağlayan bir $<$ bağıntısıdır:
$\bullet$ Her $x,y\in S$ için $x<y, x=y$ ya da $y<x$ ‘dir.
$\bullet$ Her $x,y,z\in S$ için $x<y$ ve $y<z$ ise $x<z$ ‘dir.

Bir $<$ sıralaması için, $x\leq y$ gösterimi $x<y$ ya da $x=y$ anlamına gelirken; $x>y$ gösterimi, $y<x$ ‘in bir diğer ifade ediliş biçimidir.

Şimdi $(F,+, .)$ bir cisim ve <, $F$ üzerinde bir sıralama olsun. Eğer bu sıralama, her $x,y,z\in F$ için
1) $x<y$ ise $x+z<y+z$ ,
2) $0<x$ ve $0<y$ ise $0<x.y$
özelliklerini sağlanıyorsa $F$ ‘ye bir sıralı cisim denir. Örneğin reel sayılar, üzerindeki bilinen sıralama ile bir sıralı cisimdir. Fakat kompleks sayılar üzerinde bu özelliklere sahip bir sıralama tanımlanamaz. Peki neden? Eğer böyle bir sıralama olsaydı, $i\neq 0$ olduğundan, sıralamanın özelliğinden dolayı, elimizde iki durum olurdu:
(i) i>0: Öncelikle 2’den $i.i=i^2=-1>0$ olur. Burada yine aynı özellik kullanılırsa, 1=(-1).(-1)>0 elde edilir ve bu iki durum birbiriyle çelişir.
(ii) i<0: Bu durumda 1’den $0=i+(-i)<0+(-i)=-i$ ve böylece 2’den $0<(-i).(-i)=(-1).i.(-1).i=1.i^2=-1$ olur. Burada yine 1’i kullanırsak, $1=0+1<(-1)+1=0$ elde ederiz. Diğer taraftan (i)’de gösterildiği gibi $1>0$ olacaktır, ki bu iki durum birbiriyle çelişir.

Şimdi özel bir sıralı cisim olan ve sıralı olmasının yanı sıra tamlık (completeness) gibi bir özelliği sağlayan reel sayılarla devam edelim. Bunun için önce üstten sınırlılık ve supremum kavramlarının neyi ifade ettiğinden bahsetmek gerekir. İsminden de anlaşılacağı gibi, bir $S\subseteq F$ altkümesi verildiğinde, her $x\in S$ için $x\leq b$ olacak şekilde bir $b\in F$ bulunabiliyorsa, $S$ kümesi üstten sınırlıdır denir. Tabii bu durumda $b\in F$ , $S$ kümesi için bir üst sınır olarak adlandırılır. Örneğin $S=(0,1)\subseteq \mathbb{R}$ kümesi için $b=1, b=2.5, b=125$ gibi elemanların her biri birer üst sınırdır. İşte biz bu üst sınırların en küçüğüne S kümesinin supremumu (ya da kısaca $sup S$ ) diyeceğiz. $S=(0,1)$ kümesi için $sup S=1$ olduğuna dikkat edelim. Bu örnek sayesinde bir kümenin supremumunun kümenin içinde olması gerekmediğini de görebiliriz.

İşte tamlık aksiyomu (ya da diğer ismiyle, en küçük üst sınır özelliği) diyor ki “Üstten sınırlı her kümenin bir supremumu vardır”

Tamlıkla ilgisi olmasa da, hazır yeri gelmişken supremum ve maksimum arasındaki farktan da bahsetmek gerekir. Maksimum, kümeye ait olan en büyük elemandır ve küme üstten sınırlı bile olsa, her zaman var olması gerekmez. Yine $(0,1)$ kümesini ele alırsak, bu kümenin bir maksimum elemanının olmadığını söyleyebiliriz. Çünkü hem bu kümede ikamet edip, hem de kümedeki her elemandan daha büyük olan bir eleman bulunamaz. Fakat eğer elimizde $S=(0,1]$ kümesi olsaydı, burada $sup S=maks S=1$ olduğunu söyleyebilirdik. Genel olarak bir $S$ kümesinin maksimumu varsa, $maks S=sup S$ olacağına dikkat edelim.

Reel sayılar tamlık özelliğini sağlar ve hatta tamlık aksiyomunu sağlayan her sıralı cisim birbirine izomorf olduğundan, reel sayıların, bu özelliğe sahip tek sıralı cisim olduğu söylenilebilir. Ama örneğin rasyonel sayılar tamlık aksiyomunu sağlamaz. Bunu görmek için $S=\{r\in \mathbb{Q} : r^2<2\}\subseteq \mathbb{Q}$ alt kümesini ele alalım. Öncelikle $1\in S$ olduğundan üzerinde çalışacağımız bu küme boştan farklıdır, yani ispat yaparken boşa kürek çekmiş olmayız. Ayrıca $r\in S$ için $r^2<2<16$ olduğundan $r<4$ olur. Yani kümenin bir üst sınırı vardır. Şimdi tersine, $sup S=b$ var olduğunu kabul edelim. Rasyonel sayılar sıralı bir cisim olduğundan $b^2=2$ , $b^2<2$ ya da $b^2>2$ olmalıdır. Fakat;

$\bullet$ $q^2=2$ özelliğine sahip bir $q\in \mathbb{Q}$ olmadığından $b^2=2$ olamaz.

$\bullet$ $b^2<2$ ise, rasyonel sayılar reel sayılarda yoğun olduğundan $b<q<\sqrt{2}$ olacak şekilde bir $q\in \mathbb{Q}$ vardır. Ayrıca, $q^2<2$ olduğundan $q\in S$ olması gerekir. Fakat bu durumda, kümenin bir üst sınırı olan $b$ ‘den daha büyük bir eleman bulunmuş olur ve bu durum bir çelişkiye yol açar.

$\bullet$ $b^2>2$ ise, $b>q>\sqrt{2}$ olacak şekilde bir $q\in \mathbb{Q}$ vardır. Burada $q^2>2$ olduğundan, $S$ kümesinin tanımı gereği, her $r\in S$ için $r<q$ ‘dir. Bu da aslında $q$ ‘nun $S$ için bir üst sınır olması anlamına gelir. Fakat bu durum yine bir çelişkiye yol açar, çünkü $b>q$ olduğundan, en küçük üst sınır olan $b$ ‘den daha küçük bir üst sınır bulunmuş olur.

Sonuç olarak üstten sınırlı $S$ kümesinin bir supremumu yoktur ve bu nedenle $\mathbb{Q}$ tamlık özelliğini sağlamaz.

Şu an Arşimet özelliğinden bahsetmek için gereken tüm bilgilere sahibiz:

$F$ bir sıralı cisim ve $x,y\in F$ , $x>0$ olmak üzere, $nx>y$ olacak şekilde bir $n\in \mathbb{N}$ varsa, $F$ cismi Arşimedyandır ya da Arşimet özelliğini sağlar denir.

The Archimedean Property - Infinity is Really Big

Arşimet’in orijinal metninde bu özellik $x,y$ sayılarıyla değil de, doğal olarak, büyüklüğü birbirine eşit olmayan iki doğru, yüzey ya da katılar yardımıyla ifade edilmiştir. İzini sürebildiğimiz ilk hali ise, bir önceki yazıda bahsettiğimiz Eudoxus’a aittir.

Arşimet özelliğini sağlamayan bir sıralı bir cisimde, her $\mathbb{N}$ için $n\epsilon<y$ olacak şekilde $\epsilon>0$ sayıları vardır. Dikkat edersek bu sayılar, ne kadar büyük doğal sayılarla çarpılırlarsa çarpılsın, sistemdeki hiçbir sayıyı aşamayacak kadar küçüktür. Yani aslında bu sayılar sonsuz küçük sayılardır. Dolayısıyla, Arşimet özelliğini sağlayan sıralı cisimlerde sonsuz küçük sayılara yer yoktur diyebiliriz.

Şimdi reel sayıların Arşimet özelliğini sağladığını görelim: Bunun için tersine, reel sayıların bu özelliğe sahip olmadığını, yani her $n\in \mathbb{N}$ için $nx< y$ olacak şekilde $x,y\in\mathbb{R}$ , $x>0$ sayılarının olduğunu kabul edelim. Bu durumda $A=\{nx : n\in \mathbb{N}\}$ kümesi $y$ ile üstten sınırlıdır. Bu nedenle, $\mathbb{R}$ ‘nin tamlık özelliğinden $b=sup(A)$ vardır. Burada $b-x<b$ olduğundan $b-x$ bu küme için bir üst sınır olamaz. Çünkü en küçük üst sınır $b$ ‘dir ve bundan daha küçük olan bir sayının üst sınır olması beklenemez. Şimdi aklımızda bir sayı doğrusu çizelim ve $A$ kümesini burada bir aralık gibi düşünelim. $b-x$ , $A$ kümesini üstten sınırlamıyorsa bu şu anlama gelir: $A$ ‘nın, $b-x$ ‘den büyük olan en az bir elemanı olmalıdır. Yani, $b-x<mx$ olacak şekilde bir $m\in \mathbb{N}$ vardır. Bu son eşitsizlikle biraz oynarsak, $b<mx+x=(m+1)x$ elde ederiz. Burada, $A$ kümesinin tanımı gereği $(m+1)x\in A$ olması gerekir. Fakat $A$ ‘nın bir elemanı nasıl olur da $b=sup A$ sayısından daha büyük olabilir? Demek ki bu durum bize bir çelişki verir ve bizi bu çelişkiye ulaştıran kabulün yanlış olduğunu söyleyebiliriz. Yani, reel sayılar Arşimedyandır.

Son olarak, bu özelliğe sahip olmayan sıralı cisimlerin var olduğuna dair bir örnekle konuyu kapatalım. $\mathbb{R}[x]$ , katsayıları reel sayılar olan tüm polinomların kümesini göstersin. Öncelikle, $\mathbb{R}$ bir cisim olduğundan, $\mathbb{R}[x]$ bir halkadır. Şimdi bu halkayı kullanarak, rasyonel polinomlar cismini inşa etmeye çalışalım. Bunun için, $\mathbb{R}(x)=\{\frac{p(x)}{q(x)} : p(x),q(x)\in \mathbb{R}[x], q(x)\neq 0\}$ kümesini tanımlayalım. Burada, rasyonel polinomların en sade hallerinde olduklarını ve $q(x)$ ‘in baş katsayısının 1 olduğunu kabul edelim (değilse bile, bu forma getirmek mümkündür.) İşte bu yolla edilen $\mathbb{R}(x)$ bir cisimdir. Bu cisimde bir $\frac{p(x)}{q(x)}$ elemanının pozitif olması için gerek ve yeter koşul, $p(x)$ ‘in baş katsayısının (yani en yüksek dereceli teriminin katsayısının) pozitif olması olsun. Pozitif elemanlar yardımıyla, $\mathbb{R}(x)$ üzerinde, “ $P, Q\in \mathbb{R}(x)$ için $P<Q \Leftrightarrow Q-P>0$ ” biçiminde bir sıralama tanımlayabiliriz.

Şimdi $h(x)=\frac{x}{1}\in \mathbb{R}(x)$ olsun ve Arşimet özelliğinin sağlanmadığını görmek için $h(x),1\in \mathbb{R}(x)$ ikisini ele alalım. Her $n\in \mathbb{N}$ için $h-n1=\frac{x-n}{1}$ pozitif, yani $h-n1=\frac{x-n}{1}>0$ olduğundan $n1<h$ olacaktır. İşte bu nedenle $\mathbb{R}(x)$ Arşimedyan değildir.

Farkında olmasak da Arşimet özelliğini birçok ispatta kullanıyoruz. Ama genelde yukarıdaki ifadeyi değil de, ona denk olan “Her $\epsilon>0$ için $\frac{1}{n}<\epsilon$ olacak şekilde bir $n\in \mathbb{N}$ vardır” ifadesini. En basitinden $\frac{1}{n}$ dizisinin limitinin 0 olduğunu ya da doğal sayıların üstten sınırlı olmadığı gösterirken bile bu özelliği kullanmamız gerekiyor. Oldukça uzun bir yazı olduğu için ispata girmeyelim ama sebebini merak edenler için buraya bırakalım. Son olarak teoremin tüm diğer sonuçlarını görmek isteyenler ise buraya bir göz atabilirler.

Kaynaklar
1) https://en.wikipedia.org/wiki/Ordered_field
2) https://infinityisreallybig.com/2021/01/19/definitions-of-ordered-set-and-ordered-field/
3) https://infinityisreallybig.com/2021/06/07/the-archimedean-property/
4) https://www.stumblingrobot.com/2015/07/02/prove-that-the-rationals-satisfy-the-archimedean-property-but-not-the-least-upper-bound-axiom/
5) https://www.mathcounterexamples.net/a-non-archimedean-ordered-field/
6) https://www.uobabylon.edu.iq/eprints/paper_12_27257_140.pdf
7) https://www.impan.pl/~pmh/teach/algebra/additional/nonarchimedian.pdf
8) http://users.uoa.gr/~apgiannop/Sources/Hjelmslev-1950-Centaurus.pdf

Sonsuz Küçükler: “Epiyce yaklaşmışım, duyuyorum, anlatamıyorum”

Posted on 3 Şubat 2022 by esrakorkmaz

Cevapla

$\Delta x=x-x_0$ , $x$ -koordinatındaki, $\Delta y=y-y_0$ ise $y$ -koordinatındaki değişimi göstermek üzere, bir doğrunun eğiminin $\frac{\Delta y}{\Delta x}= \frac{y-y_0}{x-x_0}$ olduğunu biliyoruz. Peki bir eğrinin eğimi ile neyi kastediyoruz? Yani örneğin $y=x^2$ parabolünün belli bir noktada eğimini bulmak ne anlama gelir? İşte bunu anlamak için önce sonsuz küçüklerin dünyasına bir giriş yapmamız gerekir.

$P=(x_0,y_0)$ ve $Q=(x_0+\Delta x, y_0+\Delta y)$ bu eğri üzerinde alınmış iki farklı nokta olmak üzere, eğrinin bu noktalar arasındaki ortalama eğimi (ya da değişimi) $\frac{\Delta y}{\Delta x}$ ‘dir. Yani aslında bu iki noktadan geçen doğrunun eğimine eşittir. Şimdi Pisagor teoreminden bu eğimin neye eşit olduğunu bulalım.

Öncelikle $P$ ve $Q$ noktaları bu eğri üzerinde olduğundan, $y_0={x_0}^2$ ve $y_0+\Delta y=({x_0+\Delta x})^2$ eşitliklerinin sağlandığını söyleyebiliriz. Burada 2.eşitliği 1. ‘den taraf tarafa çıkarırsak,

$y_0+\Delta y-y_0=\Delta y=({x_0+\Delta x})^2-{x_0}^2=2 x_0 \Delta x+(\Delta x)^2$

elde ederiz. Bu durumda ortalama eğim $\frac{\Delta y}{\Delta x}=\frac{2 x_0 \Delta x+(\Delta x)^2}{\Delta x}=2 x_0 + \Delta x$ olur. Burada son eşitliği yazmak, yani $\Delta x$ ‘leri sadeleştirebilmek için, $\Delta x\neq 0$ koşulunun sağlanması gerektiğine dikkat edelim. Çünkü aksi halde $\frac{0}{0}$ belirsizliği ile karşılaşırız.

Peki acaba $P=(x_0, y_0)$ noktasındaki eğimi nasıl bulabiliriz? Tamam, $\Delta x$ yine 0’dan farklı olsun, ama 0’a da çok yakın olsun. Yani o kadar küçük olsun ki, $Q$ noktası $P$ noktasının iyice yakınında bulunsun. İşte bu durumda, 0’a çok yakın olan bu $\Delta x$ sayısını ihmal ederek, $P$ noktasındaki eğimin $2 x_0$ değerine oldukça yakın olacağını söyleyebiliriz. Bu durumda örneğin $(2,4)$ noktasındaki eğim yaklaşık olarak 4’e eşit olacaktır.

Burada asıl sorun bu “ihmal etme” işini neye göre yaptığımız. Yani hangi sayılar ihmal edilecek kadar küçük, hangileri değildir? İşte bir matematikçi olarak bize düşen, her zaman yaptığımız gibi, buna bir standart getirmek ve bir tanım yapmaktır.

Eğer her $a\in \mathbb{R}$ için $-a<\epsilon <a$ oluyorsa, bu $\epsilon$ sayısına sonsuz küçük (infinitely small, infinitesimal) denir.

Burada, sonsuz küçüklerin birer reel sayı değil, her pozitif reel sayıdan daha küçük olan yeni bir sayı türü olduklarına dikkat edelim. Farklı isimlerle de olsa, sonsuz küçük kavramının kullanımı çok eskilere dayanır. Arşimet ve hatta ondan yaklaşık iki asır önce Eudoxus, eğrilerle sınırlı bir bölgenin alanını bulmak için, bu bölgeyi, alanı bilinen küçük ve oldukça fazla bölgeyle doldurma yöntemini kullanmışlardır. Hatta ileri Analiz derslerinden tanıdık gelecek ve bir sonraki yazıda bahsedeceğimiz Arşimet (Archimedean) özelliği de aslında yine sonsuz küçüklerle ilgilidir. Bu özelliği sağlayan (örneğin reel sayılar gibi) bir sistemde sonsuz küçükler yoktur.

17. yüzyılda büyük gökbilimci Johannes Kepler, ikinci düğünü için malzeme satın alırken, tüccarların şarap fıçısının içindeki şarap miktarını belirlemek için kullandıkları yanlış yöntemlerden memnun kalmamıştır. Bunun üzerine, konik kesitlerin bazı eksenler etrafında döndürülmesiyle elde edilen yaklaşık 100 dönel cismin hacmini bulmaya çalışmıştır.

Kepler, hacim hesabı yapmak için sonsuz küçük geometrik nicelikler kullanmıştır. Örneğin, şarap fıçısının her biri silindir olan tabakalardan oluştuğunu düşünmüş ve hacmini hesaplamak için bu tabakaların hacimlerini toplamıştır.

Kepler’in bu buluşu ışığında, İtalyan matematikçi Bonaventura Cavalieri, 1635 yılında alanları ve hacimleri hesaplamak için bölünmezler (indivisibles) yöntemini ortaya koymuştur. Bölünmezler, bulunduğu cismin/şeklin bir boyut düşüğünde yaşarlar. Örneğin, bir kitabın sayfalarını iki boyutlu olarak düşünürsek, bu iki boyutlu bölünmezler yardımıyla üç boyutlu bir kitabın hacmini hesaplayabiliriz. Tıpkı günümüzde integral hesabında yaptığımız gibi.

Sonsuz küçükler, Newton ve Leibniz’in kalkülüsünde de kullanılmışlardır. Örneğin diferansiyel dediğimiz şey aslında bir değişkendeki sonsuz küçük değişimleri temsil eder. Aşağıdaki videoda, limit kullanmadan, sadece sonsuz küçükler yardımıyla $\sin(x)$ fonksiyonunun türevinin $\cos x$ olduğunun gayet güzel bir ispatı mevcut. Newton, Leibniz ve sonrasında gelen birçok kişi, kalkülüse tıpkı bu şekilde, yani sonsuz küçüklerin işin içinde olduğu sezgisel yollarla yaklaşmışlardır.

Sonsuz küçük kavramı öyle sezgiseldir ki, var olduklarını kabul etsek bile tam olarak ne oldukları hakkında bir fikir sahibi olamayız. Yani öyle bir şey ki; “Bir sayı var biliyoruz. Epiyce yaklaşıyoruz, duyuyoruz, anlatamıyoruz.” Şu an bile aklımızı böylesine zorlayan bu kavram, haliyle o zamanlar da birçok itiraza sebep olmuştur. Örneğin George Berkeley, The Analyst isimli kitabında sonsuz küçükleri “ölmüş niceliklerin hayaletleri” olarak tanımlamıştır ve ayrıca

“Ne kadar küçük olursa olsun bir şey ihmal ediliyorsa, hızın kesin bir değere değil ancak yaklaşık bir değere sahip olduğunu söyleyebiliriz. (…) Artışların yok olduğunu varsayıyorsak, artışların var olduğu yönündeki ilk varsayım terk edilmiş demektir, bu durumda o ilk varsayımın sonuçlarından biri sayesinde elde edilmiş bir sonuçla karşılaşırız, ki bu da yanlış bir akıl yürütmedir.”

diyerek tepkisini ortaya koymuştur. Fakat biliyoruz ki, tüm bu itirazlara rağmen, sonsuz küçüklere dayalı integral ve türev hesabı şuan bile geçerliliğini koruyor. Hatta Abraham Robinson sayesinde, bugün sonsuz küçükleri kullanarak da kalkülüs yapılabilineceği biliniyor. Robinson’un ortaya koyduğu ve standart olmayan (non-standart) analiz ismiyle bilinen bu sistem, tüm reel sayıları ve 0 dışındaki tüm sonsuz küçükleri içeren Hiperreel Sayılar üzerine kurulmuştur. Kalkülüsün sonsuz küçükler yardımıyla baştan sona nasıl inşa edildiğini merak edenler, H. Jerome Keisler’ın bu konuda yazılmış oldukça kapsamlı kitabına buradan ulaşabilirler. Modern analize büyük ölçüde yön vermiş olan sonsuz küçükleri anlamak, hem birçok fikrin nasıl doğduğuna şahit olmamızı sağlayacak, hem de aslında neyi ifade etmeye çalıştıklarını anlamamızı kolaylaştıracaktır.

Kaynaklar
1) M.T. Carroll, S.T. Dougherty, D.Perkins, Indivisibles, Infinitesimals and a Tale of Seventeenth-Century Mathematics, Mathematics Magazine, 86, 239–254, 2013.
2) https://people.math.wisc.edu/~keisler/calc.html
3) https://infinityisreallybig.com/2019/11/30/infinitesimal-calculus-and-calculus-rules/
4) http://amsi.org.au/ESA_Senior_Years/SeniorTopic3/3a/3a_4history_3.html
5) https://www.maa.org/press/periodicals/convergence/kepler-the-volume-of-a-wine-barrel-introduction

Topolojik bir oluşum!

Monthly Archives: Şubat 2022

Ütopya Sevenlere: Düzülke

Explained: Arşimet (Archimedean) Özelliği

Sonsuz Küçükler: “Epiyce yaklaşmışım, duyuyorum, anlatamıyorum”