Evliliğin Matematiği

Rönesans’ın en büyük gök bilimcilerinden biri olan Johannes Kepler, eşi Barbara’yı koleradan kaybettikten sonra ikinci bir evlilik yapmaya karar verir. İlk evliliğinde mutluluğu yakalayamadığından olsa gerek, ikincisine bir matematikçi titizliği ile yaklaşmayı düşünür. 11 adayla görüşmeler yapar ve her birinin artı ve eksilerini not ederek bir evlilik stratejisi bulmaya çalışır.

Tüm bunlardan üç asır sonra Arthur Cayley (1821-1895), Kepler’in yapmaya çalıştığı istatistiksel eş seçiminin ardındaki matematiği inceler. Cayley, evlilik sorununun aslında optimal durma (optimal stopping) teorisi olarak adlandırılan bir sorun olduğunu belirtir. Yani aslında işin özü, kaç adayla görüştükten sonra görüşmelere bir son vereceğimizi saptamaktır. İşte matematikçilerin de bu konuda bazı teşebbüsleri olmuştur ve sekreter problemi (secretary problem), telaşlı talip problemi (fussy suitor problem) ya da sultanın çeyizi problemi (sultan’s dowry problem) gibi farklı isimlerle bilinen bir problem ortaya koymuşlardır. Buna göre yapmanız gereken şey, tüm ciddi adayların sayısını 2.71828’ye (yani e sayısına) bölmektir. Daha sonra, o sayıya kadar olan adaylardan daha iyi olduğunu düşündüğünüz ilk adayla hayatınızı birleştirebilirsiniz. Gayet kolay değil mi 🙂 Şu an biliyoruz ki, hayatının iki yılını bu seçime adayan Kepler’in tek yapması gereken, 5. adaydan sonra kararını bir an önce vermekti.

Evlilik söz konusu olduğunda teoremler bununla bitmiyor. Şimdi sırada, kiminle evleneceğimizden ziyade, bir eşlemenin mümkün olup olmadığına karar vermemize yardımcı olacak olan Hall’ın evlilik teoremi var. Bu teorem bize, elimizde belli sayıda kadın ve erkek adayın arasındaki olası eşleşmelerin bir listesi olduğunda, herkesin uygun bir eşleşmeyle evlenebilmesinin mümkün olması için, listenin hangi özellikleri sağlaması gerektiğini söylüyor. Teoremi ifade etmeden önce SDR kavramından bahsedelim.

$\{A_1, A_2, \ldots A_n\}$ , bir $A$ kümesinin alt kümelerinden oluşan bir aile olsun. Bu durumda,
(i) $x_i\in A_i, i=1,2\ldots n$ ,
(ii) $x_i\neq x_j, i\neq j$
koşulunu sağlayan $(x_1, x_2,\ldots x_n)$ elemanlarından oluşan bir sisteme farklı temsilciler sistemi (system of distinct representatives ya da SDR) denir.

Verilen her küme ve onun alt kümelerinden oluşan bir aile için, yukarıdaki gibi bir seçim yapmak her zaman mümkün değildir. Örneğin $A_1=\{x,y\}, A_2=\{x,y\}, A_3=\{x,y\}$ veya $A_1=\{x,y\}, A_2=\{x,y\}, A_3=\{x,y\}, A_4=\{y,z,t,w\}$ ailelerinin her ikisinden de bir SDR seçilemez. Çünkü seçilen ilk 3 elemanın birbirinden farklı olmalarının imkanı yoktur.

Yukarıdaki her iki durumda da bir SDR bulamamızın sebebini şöyle açıklayabiliriz. Bize verilen kümelerden keyfi sayıda seçelim. Örneğin ikinci örnekte $A_1, A_2$ ve $A_3$ kümelerini alalım. Bu kümelerden seçilebilecek olası temsilcilerin sayısını bulalım, yani aslında kümelerin birleşiminde kaç eleman olduğuna bakalım. Örneğimizde seçilebilecek temsilciler x ve y elemanlarıdır. İşte elimizdeki kümelerin sayısı, bu temsilcilerin sayısından çok olduğundan bir SDR elde edemiyoruz. Çünkü burada $\mid A_1\cup A_2 \cup A_3 \mid=2<3$ oluyor.

Peki hangi koşullar altında böyle bir SDR bulmak söz konusudur. Bu sorunun cevabı, iki büyük dünya savaşı görmüş ve grup teori üzerine çalışmalar yapmış İngiliz matematikçi Philip Hall’dan geliyor.

$\{A_1, A_2, \ldots A_n\}$ kümelerinden oluşan bir ailenin bir SDR’ye sahip olması için gerek ve yeter koşul her $\{i_1,i_2,\ldots, i_k\}\subseteq \{1,2,\ldots, n\}$ kümesi için $\mid \bigcup_{j=1}^k A_{i_k}\mid \geq k$ olmasıdır.

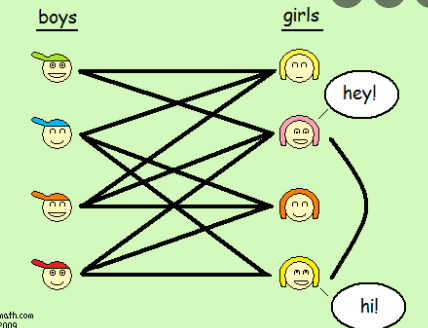
Peki Hall’ın elde etmiş olduğu bu sonucun evlilik teoremi olarak bilinmesinin sebebi nedir? Bunu görmek için erkeklerden oluşan sonlu bir küme alalım. Bunların her birinin tanıyor olduğu kızların kümesinin de sonlu olduğunu varsayalım. Acaba hangi koşul altında her bir erkeğin tanışıyor olduğu kızlardan biriyle evlenmesi mümkündür? Burada erkeklerin sayısı n ise ve j. erkeğin tanışıyor olduğu kızların kümesi $A_j$ ile gösterilirse, soru yukarıdaki teoreme kolayca uyarlanabilir. O halde istenilen koşulun sağlanması için, seçilen her $k<n$ erkek için, erkeklerin tanıyor oldukları kızların toplamının erkeklerin sayısından fazla olması gerekir.

İlgilenenler için, teoremin güzel bir ispatı burada mevcut. Bunun yanı sıra, çizge teorisi veya lineer cebir kullanarak yapılan ispatlar da oldukça popüler. Fakat bence işin en güzel kısmı, çok alakasız görünse bile, teoremin sadece genel topoloji bilgisi kullanılarak bile ispatlanabiliyor olması. Şimdi durumu biraz daha zorlaştıralım ve sonsuz sayıda erkek olduğunu varsayalım. Fakat her bir erkeğin tanıyor olduğu kızların sayısı yine sonlu olsun. $B$ tüm erkeklerin kümesi ve her $b\in B$ için $G(b)$ , $b$ ‘nin tanışık olduğu kızların kümesi olsun. Her bir $G(b)$ kümesini ayrık topoloji ile ele alalım. Bu durumda her $G(b)$ , kompakt Hausdorff bir uzay olacaktır. O halde Tychonoff Teoremi‘nden $G=\Pi_{b\in B} G(b)$ kartezyen çarpımı da kompakt bir kümedir. Şimdi keyfi sonlu $\{b_1, b_2\ldots, b_n\}$ kümesi için

$H=\{g\in G : i\neq j \hspace{0.1cm} (i, j=1,2,\ldots n) \hspace{0.1cm} \textrm{i\c{c}in} \hspace{0.1cm} b_i\neq b_j \}$

kümesini tanımlayalım. Önce H’nin kapalı bir küme olduğunu gösterelim: $G_i \times G_j$ kümesi sonlu ve ayrık bir uzaydır. (Sonsuz sayıda ayrık topolojik uzayın çarpımı ayrık olmasa da, sonlu durumda bu iş mümkün.) Bu nedenle bu uzayın her alt kümesi kapalıdır. (Çünkü ayrık uzayda her alt küme hem açık hem de kapalıdır.) $G_{ij}=\{(x,y) : x\neq y\}\subseteq G_i\times G_j$ ve $p: G\rightarrow G_i\times G_j$ izdüşüm fonksiyonu olmak üzere, $H_{ij}=p^{-1}(G_{ij})\subseteq G$ kümesi $G$ uzayında kapalıdır. Çünkü bu küme, kapalı bir kümenin sürekli bir fonksiyon olan p altındaki ön görüntüsüdür. Ayrıca $H=\bigcap_{i,j} H_{ij}$ olduğundan H da kapalı bir kümedir.

Elimizde her sonlu $\{b_1, b_2\ldots, b_n\}$ için bir H kümesi olur. İşte bu H kümelerinin ailesi sonlu arakesit özelliğini sağlar, yani sonlu sayıda H kümesinin kesişimi yine sonlu olur. Çünkü işin temelindeki $G(b)$ kümeleri zaten sonludur.

Bir uzay kompakt ise, sonlu arakesit özelliğine sahip kapalı kümelerden oluşan her aile için, bu ailenin tüm elemanlarının kesişiminin boştan farklı olduğunu biliyoruz. Bu nedenle tüm H kümelerinin kesişimi boştan farklıdır. O halde kesişimde $b\neq b'$ için $g(b)\neq g(b')$ olacak şekilde bir eleman vardır. İşte bu elemanın varlığı bize tüm erkeklerin farklı biriyle evlenebilmesinin mümkün olduğunu söyler. Yani her $b$ kişisinin evleneceği bir $g(b)$ vardır ve her $b$ ‘ye farklı bir $g(b)$ karşılık getirilebilir.