Sanat sanat için oluyor da neden “matematik matematik için” olmasın? Binlerce yıl boyunca hesap kitap, zaman-takvim, miras dağılımı, inşaat işleri filan derken “işe yarar” şeylerde yeterince kullanılmış (ve hala da kullanılmakta olan) matematiğin biraz da günlük yaşamdan uzaklaşıp sezgilere aykırı işlerle uğraşmaya hakkı yok mu? Isaac Asimov, Matematikçinin Galaksi Rehberi kitabının önsözünde bu tür işleri hayal gücü için yaratıcı bir sığınak olarak nitelendiriyor ve diyor ki:
İşte şimdi bahsedeceğim konu, olağan dışı ve sezgilere aykırı olarak görülen ve ayrıca, evrensel olarak geçerli olduğu düşünülen bazı teoremleri ihlal etmek için özel olarak oluşturulmuş “patolojik nesneler”.
Sürekli bir fonksiyon denildiğinde akla gelen ilk şeyin “grafiğini, kalemimizi kaldırmadan çizebileceğimiz” bir fonksiyon olduğunu biliyoruz. Yani sezgisel olarak, sürekli bir fonksiyon sıçramaları (jumps) olmayan bir fonksiyondur.
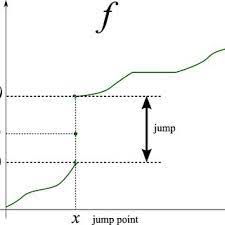
Diğer taraftan, bir fonksiyonun bir noktada türevlenebilir olması, o noktada bir teğet doğrusunun bulunabilmesidir. Bunu ise, kabaca, fonksiyonun o noktada bir köşesinin (corner) veya sivri ucunun (cusp) olmaması olarak yorumlayabiliriz.
19. yüzyılın ortalarına kadar matematikçiler arasındaki genel inanış, sürekli bir fonksiyonun türevlenemediği noktalar olsa da, bunların arasında mutlaka türevlenebilirliğin sağlandığı parçaların var olduğu yönündeydi. (Örneğin testere dişlerinin oluşturduğu fonksiyonu düşünelim.)
Hatta bu iddia Fransız matematikçi Andre Marie Ampere tarafından da ispatlanmıştır. Fakat Ampere, türevlenebilirliğin sağlandığı bölümler sonsuz küçüklükte olursa neler olacağını düşünmemiş ve hatta buna gerek olmadığını iddia etmiştir. 1860’larda ortalıkta gezinen söylentiler Ampere’nin yaptıklarına olan güveni sarsmaya başlamıştır. Konuşulanlara göre, Riemann öğrencilerine hiçbir noktada türevlenemeyen sürekli bir fonksiyon bildiğini söylemiş fakat bu konuda bir ispat yayınlamamıştır. Yalnızca Ampere’nin değil birçok çağdaşının sahip olduğu popüler inanışı sona erdiren şey ise Weierstrass’ın 1872 yılında yarattığı her yerde sürekli fakat hiç bir yerde türevlenebilir olmayan “canavar” olmuştur. Şimdi bu fonksiyona bir bakalım:
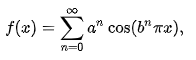
fonksiyonun sürekliliği Weierstrass M-testinden gelir. 
Weierstrass’ın canavarı olarak da bilinen bu sevimli(!) yaratığın ismini ne kadar hak ettiği gayet ortada sanırım:
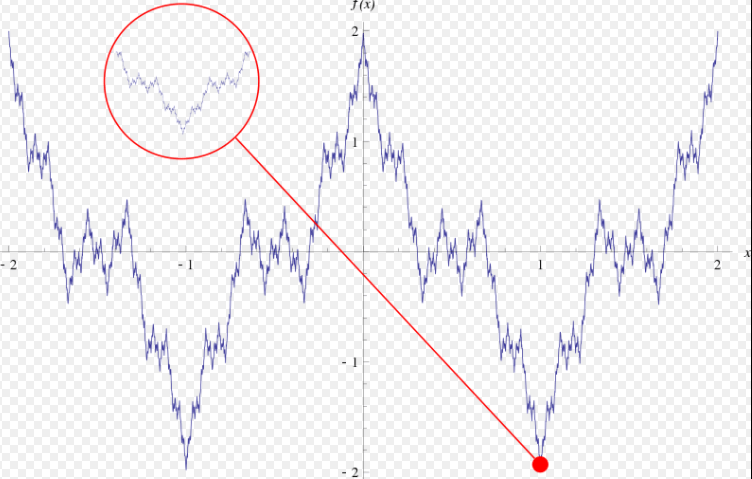
Günümüzde bilgisayarlar yardımıyla kolayca görselleştirilebilen bu fonksiyon, o zamanlar neye benzediği bilinmeyen, sezgilerle açıklanamayan bir ucube olarak nitelendirilmiştir. Weierstrass’ın, çoğu matematikçiye yabancı olan ispat tekniği de bunu iyice pekiştirmiş ve matematik çevrelerinde oldukça yankı getirmiştir. Émile Picard,”Newton böyle bir fonksiyonun varlığını bilseydi, kalkülüsü hiç icat etmezdi” demiştir. Bu tür fonksiyonları canavar olarak adlandıran ilk kişi olan Henri Poincaré ise, Weierstrass’ın fonksiyonunun sağduyuya karşı bir hakaret olduğunu, atalarımızın mantığının hatalı olduğunu göstermek için bilerek bulunduğunu söylemiş ve faydasız olduğunu iddia etmiştir.
Peki tüm bunlardan sonra ne mi olmuş? Aynı Asimov’ın değindiği gibi, bu fonksiyon birçok yerde kullanım alanı bulmuştur. Örneğin Albert Einstein 1904 yılında bir sıvıdaki parçacıkların rastgele hareketi üzerine tanımladığı Brownian hareketi teorisinde Weierstrass’ın fonksiyonunu kullanmıştır. Çünkü su moleküllerinin çarpışmaları öyle sıktır ki izledikleri yörünge asla düzgün (smooth) olmaz ve bu nedenle hiçbir yerde türevlenemez.
Geometriden finansa birçok alanda kullanılmış olan bu fonksiyon, patolojik nesnelerin en güzel örneklerinden biridir. İsterseniz artık beynimize daha fazla işkence etmeyelim ve diğer örnekleri bir sonraki yazıya bırakarak, ustaya en içten saygılarla konuyu noktalayalım.
Kaynaklar
Topolojik bir oluşum! 