Peçete Halkası Paradoksu

Posted on by
Chateau Wooden Napkin Ring | Pottery Barn

Bundan yıllar yıllar önce, yemek yeme işi yalnızca karın doyurma amaçlı yapılırken, genel yiyici kitlesi sunumsuz yakalanma telaşına düşmemiş ve dahi peçete halkası bile icat edilmemişken, Japonya’da Edo döneminde yaşamış bir zat-ı muhteremin bugün Peçete Paradoksu (Napkin Ring Paradox) olarak bilinen problemden ilk olarak bahsettiği rivayet olunur. Peki nedir Peçete Paradoksu?

Elimizde herhangi bir küre olsun. Bu kürenin içini bir silindirle oyup çıkartıyoruz ve peçete halkasına benzeyen bir cisim elde ediyoruz. İddia şu: Farklı yarıçaplara sahip kürelerden elde edilen peçete halkalarının, yükseklikleri eşit oldukları sürece hacimleri de eşittir.

Küremiz ceviz, kavun ve hatta Dünya büyüklüğünde olabilir. Eğer yükseklikler eşitse, hacimler mutlaka eşit olacaktır. Küçük olandan elde edilenin daha kalın bir halkası olacak, ancak her biri tam olarak aynı hacme sahip olacaktır. Gelin bunu iki farklı yöntem kullanarak hesaplayalım.

Şekil I

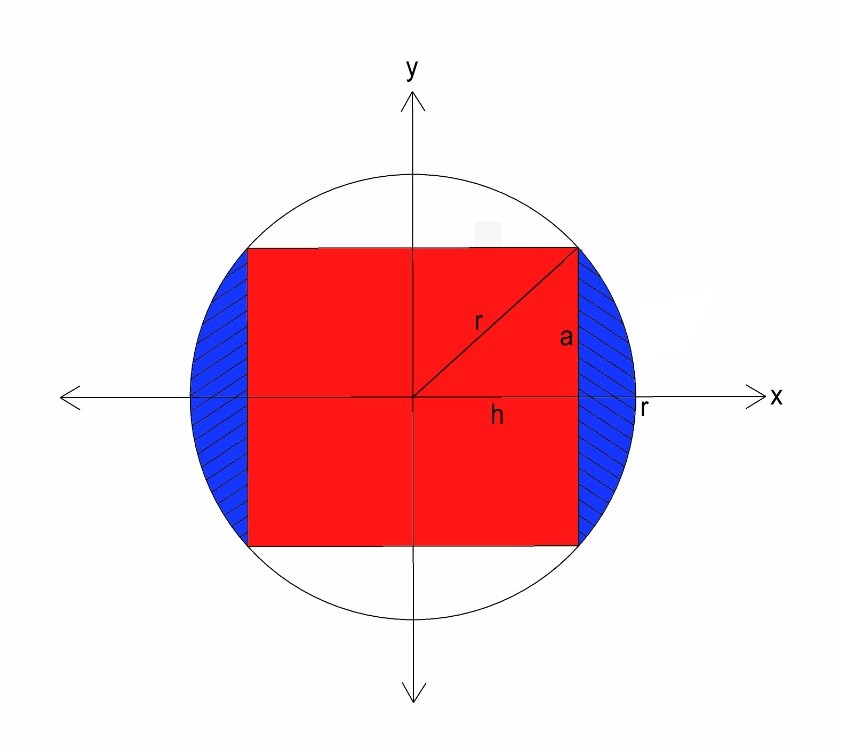
Yukarıdaki şekilde, içinden a yarıçaplı silindir çıkarılmış r yarıçaplı bir kürenin merkezi bir kesiti gösterilmektedir. Burada peçete halkasının hacmini (V) hesaplamak için kürenin hacminden silindirin hacmini (kırmızı kısım) ve ayrıca sağ ve solda kalan küçük parçaların hacmini (mavi kısımlar) çıkarmamız gerekir. Yani,

V= \frac{4}{3}\pi r^3-2\pi a^2 h-(Mavi kısmın hacmi)

(Burada silindirin yüksekliği 2h olduğundan hacmi \pi a^2 (2h)=2\pi a^2 h olur.)

Mavi kısımlardan birinin hacmini hesaplamak için disk yöntemini kullanırsak,

Şekil II

\int_{h}^{r} \pi (r^2-x^2) dx= \pi \left[r^2 x-\frac{x^3}{3}\right]_h^r =\pi \left [\frac{2r^3}{3}-r^2h+\frac{h^3}{3}\right]

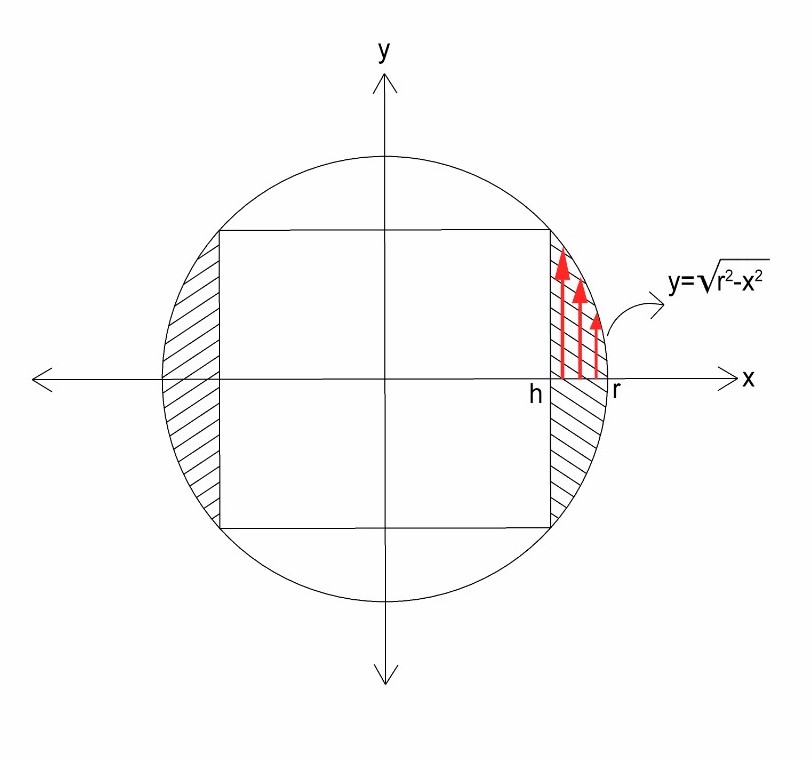
elde ederiz. (V’yi hesaplarken bunu 2 ile çarpmamız gerektiğini unutmayalım!) O halde Şekil I’den kolayca görebileceğimiz a^2= r^2-h^2 eşitliğini de kullanarak,

V=\frac{4}{3}\pi r^3- 2\pi a^2 h-\frac{4}{3}\pi r^3+2\pi r^2 h-\frac{2}{3}\pi h^3
= \pi (2r^2 h-2h a^2- \frac{2}{3}h^3)= \pi (2r^2 h-2h (r^2-h^2)- \frac{2}{3}h^3)= \frac{4}{3} \pi h^3

buluruz. Demek ki hacmi hesaplanırken yalnızca yükseklik kullanılır ve bu nedenle yüksekliklerin eşit olması, hacimlerin de eşit olması anlamına gelir.

Şimdi ikinci yönteme bir bakalım. Bunun için önce Cavalieri Prensibini öğrenelim/hatırlayalım.

Cavalieri's principle

Yukarıdaki gibi eşit yükseklikte iki katı cismimiz olsun. Eğer bunların birbirine karşılık gelen kesit alanları eşitse, hacimleri de birbirine eşittir. İntegralin uygulamalarında, kesit alma yöntemini kullanırken yaptığımız şey de tam olarak budur. Kesit alanlarını hesaplarız ve integral yardımıyla bunları toplayıp hacmi buluruz. Şimdi bu prensibi uygulayarak sonuca ulaşmak için aşağıda gösterilen kesitin alanını bulmaya çalışalım.

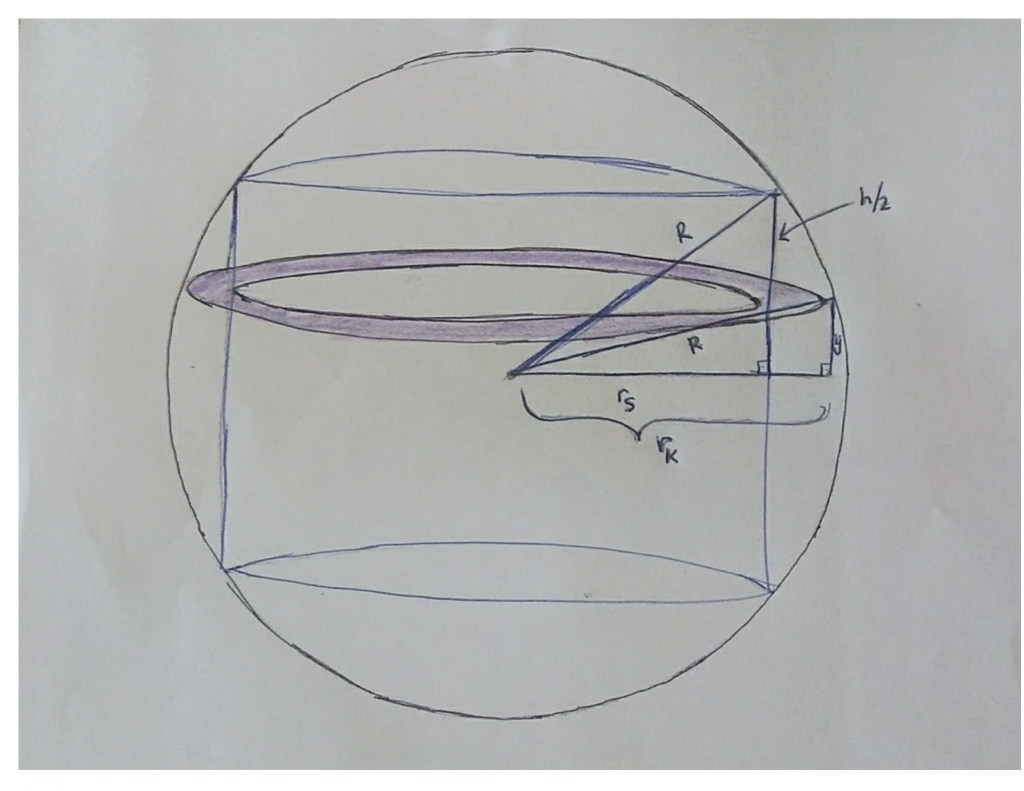
Burada R=Kürenin yarıçapı, r_k=Kesitin dış yarıçapı, r_s=Silindirin ve dolayısıyla kesitin iç yarıçapı, h= Silindirin yüksekliği ve y= Ekvatorun üstünden alınmış enine kesitin yüksekliği olsun. Kesit alanını bulmak için \pi {r_k}^2-\pi {r_s}^2 işlemini yapmamız, yani büyük dairenin alanından küçük dairenin alanını çıkarmamız gerekir.

Pisagor teoremini kullanarak, {r_s}^2=R^2-(\frac{h}{2})^2 ve {r_k}^2= R^2-y^2 olduğunu görebiliriz. Demek ki ,

Kesit alanı \pi(R^2-y^2)-\pi(R^2-(\frac{h}{2})^2)=\pi((\frac{h}{2})^2-y^2) olarak bulunur. Peçete halkalarının yükseklikleri, yani h değerleri eşit olacağından, birbirine karşılık gelen kesit alanları da eşit olacaktır. (Birbirine karşılık gelen kesitler alındığında y‘lerin de eşit olacağına dikkat edelim.)

Bu problemin bir paradoks olarak nitelendirilmesinin nedeni, çakıl taşı ve Dünya büyüklüğündeki kürelerden elde edilen peçete halkalarının hacimlerinin eşit olduğu gerçeğini sezgilerimizin kabul etmemesidir. Unutmayalım, sezgiler bizi yanıltabilir fakat matematik ve bilim bizi çoğu zaman gözlemle ulaşamayacağımız sonuçlara götürür.

KAYNAKLAR
1) https://www.maa.org/external_archive/devlin/NapkinRing.pdf
2) https://www.youtube.com/watch?v=J51ncHP_BrY
3) https://en.wikipedia.org/wiki/Napkin_ring_problem

Yorum bırakın