Ev Yapımı İspat: Buffon’un İğneleri ile Pi Sayısı Hesabı

Posted on by

Mısır’dan Mezopotamya’ya, Çin’den Antik Yunan’a bilimle uğraşan birçok kişinin gözdesi olan \pi sayısını hesaplamak, yani aslında yaklaşık bir değer bulmak için kullanılabilecek yöntemlerden biri de Georges-Louis Leclerc, Comte de Buffon’un iğne problemidir.

L uzunluğunda bir iğnenin, eşit aralıklı paralel çizgilerle kaplı bir kağıt parçasına düştüğünü varsayalım. İğnenin bu çizgilerden birini kesme olasılığı nedir?

Oldukça alakasız görünüyor ama biraz olasılık biraz da integral bilgisi kullanarak, bu problemden \pi‘nin yaklaşık değerini hesaplamamızı sağlayan bir formül elde edebiliyoruz.

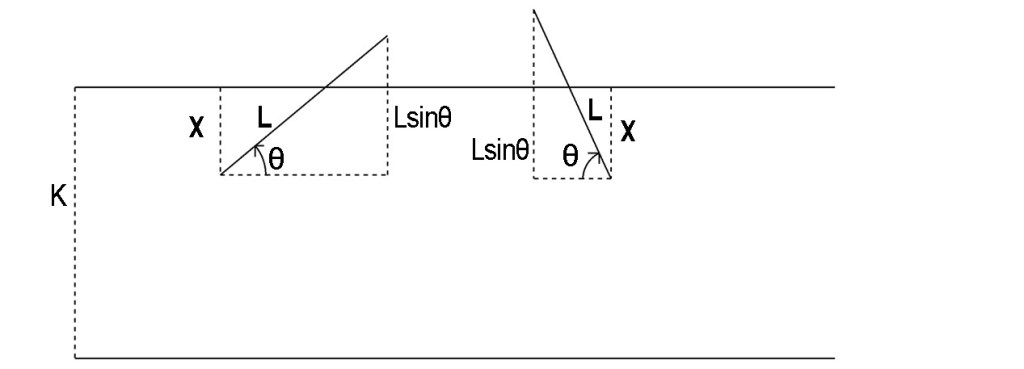
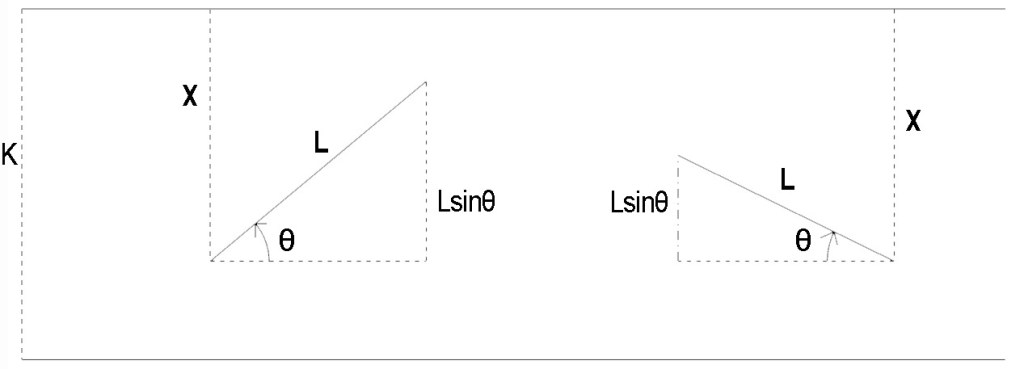
Diyelim ki, elimize L uzunluğunda bir iğne aldık ve paralel doğrular arasındaki uzaklığı da K olarak belirledik. Şimdi kağıdımızı düz bir zemine yerleştirip üzerine iğneyi atalım. İğnenin alt ucu ile üst çizgi arasındaki uzaklığa x diyelim. Daha sonra, iğnenin alt ucundan geçen ve çizgilere paralel olan bir doğru çizelim ve bu doğru ile iğne arasındaki dar açıyı \theta ile gösterelim. (Burada, K ve L sabit iken x ve \theta‘nın değişken olduğuna dikkat edelim.) Yukarıdaki şekilden görebileceğimiz gibi L \sin(\theta)> x ise iğne çizgilerden birini keser, yani başarılı bir atış yapmış oluruz.

Ayrıca burada 0\leq \theta \leq \frac{\pi}{2} ve 0\leq x\leq K olduğundan, aşağıdaki dikdörtgen örneklem uzayımızı verir.

K ve L’yi karşılaştırdığımızda iki durum elde ederiz. K>L ya da K\leq L. İlk durumu varsayıp hesaplamaları yaptığımızda \pi‘nin yaklaşık değerine ulaşabiliyoruz, bu nedenle ikinci durumu incelememize gerek kalmıyor. (Çünkü burada asıl amacımız iğnenin çizgileri kesme olasılığını hesaplamak değil, sadece \pi sayısına bir yaklaşım yapmak.) O halde K> L olduğunu kabul edelim.

Şimdi burada iğne probleminin çözümüne bir es verip biraz olasılık bilgisi ile davam edelim ve klasik olasılık ile ampirik olasılığın ne olduğunu anlamaya çalışalım.

Klasik (veya teorik) olasılık, bir örneklem uzayındaki her bir sonucun eşit olasılıkla ortaya çıkması durumlarında kullanılır. E olayı için klasik olasılık,

formülü ile hesaplanır. Diğer taraftan ampirik (veya istatistiksel) olasılık, olasılık deneylerinden elde edilen gözlemlere dayanır ve

formülü ile hesaplanır. Yazı-tura örneği üzerinden olaya açıklık getirmeye çalışalım. Bir parayı 20 kez attığımızı ve bunlardan 3 tanesinde tura geldiğini varsayalım. Bu durumda tura gelmesinin teorik olasılığı \frac{1}{2} iken, ampirik olasılığı \frac{3}{20}‘dir. Ayrıca Büyük Sayılar Kanununa göre, deney ne kadar çok tekrar edilirse ampirik olasılık teorik olasılığına o kadar yaklaşır. Yani yine bozuk para örneğini ele alırsak, parayı daha çok atarsak, teorik olasılık değeri olan \frac{1}{2}‘ye o kadar yaklaşırız.

O zaman sorumuza dönelim ve önce iğnenin paralel çizgilerden birini kesmesi olayının teorik ve ampirik olasılıklarını bulmaya çalışalım. Bunun için f(\theta)= L \sin(\theta) fonksiyonunu tanımlayalım.

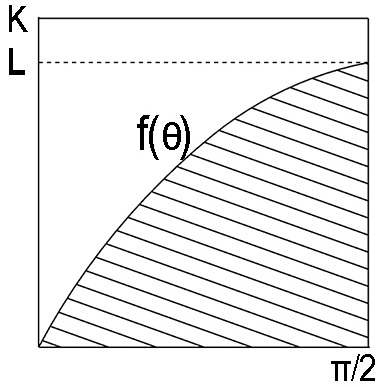
f(\theta)= L \sin(\theta)> x olduğunda iğnenin çizgiyi kestiğinden bahsetmiştik. Bu durum, yukarıdaki grafikte taralı kısma denk gelir. O halde iğnenin çizgiyi kesmesi olayının teorik olasılığı, P=taralı bölgenin alanı / tüm dikdörtgenin alanı olur.

Ön izleme(yeni sekmede açılır)

Taralı bölgenin alanı P=\int_0^ \frac{\pi}{2} L \sin(\theta) \,d\theta=L , tüm dikdörtgenin alanı ise \frac{K \pi}{2} olduğundan P=\frac{2L}{K \pi} olarak bulunur.

Diğer taraftan, eğer \widehat{P}, iğnenin çizgiyi kesmesi olayının ampirik olasılığı ise \widehat{P}\approx \frac{2L}{K \pi} yani \pi \approx \frac{2L}{K \widehat{P}} olur.

Formülümüzü elde ettiğimize göre artık deneye başlayabiliriz. L=4 cm, K=6 cm olsun. İğneyi 100 kez atalım ve başarılı atış sayımız da 41 olsun. Bu durumda,

\pi \approx \frac{2\times 4}{6\times \frac{41}{100}}= 3.25203 elde edilir.

Burada daha fazla atış yapmış olsaydık Büyük Sayılar Kanununa göre \pi sayısına daha yakın bir değer elde etmiş olurduk. Biraz boş vaktiniz varsa denemek eğlenceli olabilir ama eğer yoksa buraya buyurun.

Kaynaklar

(1) Lee L. Schroeder, Buffon’s needle problem: An exciting application of many mathematical concepts, The Mathematics Teacher, Vol. 67(2), (1974),183–186.
(2) https://acikders.ankara.edu.tr/pluginfile.php/102233/mod_resource/content/0/%C4%B0statistik%20Ders%20Notu%204.pdf

Yorum bırakın