Hausdorff Metriğinden Fraktal Görüntü Sıkıştırma Teknolojisine

Nesneler arasındaki uzaklıktan anladığımız şey genelde onlar arasındaki en kısa mesafedir. Örneğin bir doğrunun bir düzleme ya da iki düzlemin birbirine olan uzaklığını bulurken, bu iki kümenin noktaları arasındaki minimum uzaklığı elde etmeye çalışırız. Peki bu, iki nesnenin birbirine yakın olduğunu söylemek için yeterince iyi bir yöntem midir? Yani, bu nesneler birbirlerine oldukça yakın birer noktaya sahip olmalarına rağmen, diğer noktalar için bu durum geçerli olmayabilir mi?

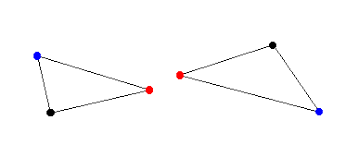
Örneğin yukarıdaki şekilde, iki üçgen arasındaki uzaklık değeri küçük olabilir, fakat şeklin geneline bakıldığında, bu değerin, mavi noktaların birbirine oldukça uzak olduğu gerçeğini yansıtmadığı açıktır. Şimdi yukarıdaki üçgenleri, aralarındaki uzaklık değişmeyecek şekilde, aşağıdaki gibi yeniden konumlandıralım.

Burada, konum değişmesine rağmen uzaklığın aynı kaldığını, dolayısıyla en kısa uzaklık kavramının nesnelerin konumundan tamamen bağımsız olduğu görebiliriz. Konu uygulamaya geldiğinde bu pek de istenilen bir özellik değildir. Neyse ki bu eksikliği ortadan kaldırmaya yardımcı olacak Hausdorff metriği vardır.

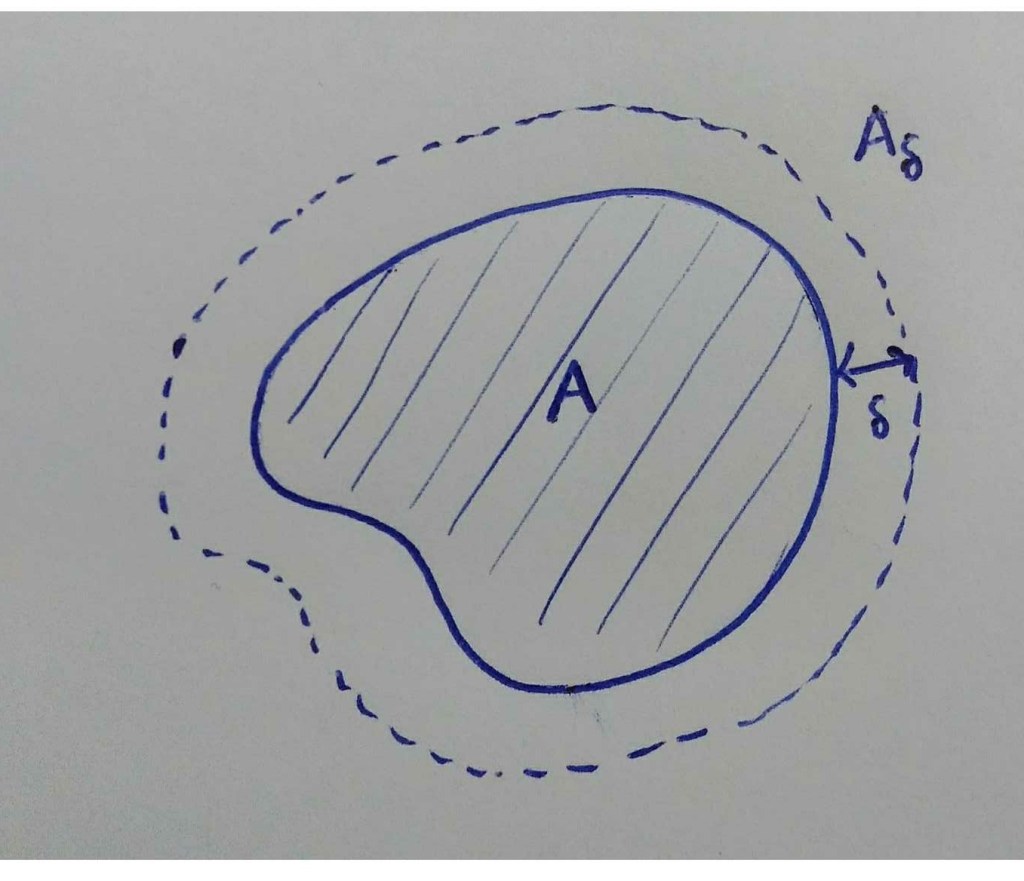
Hausdorff metriğin tanımını vermeden önce, bu metriğin neyi ölçtüğüne bir bakalım. İlk olarak çalışacağımız kümelerin kompakt olduğunu kabul edelim. $A\subseteq \mathbb{R}^2$ için, bu kümeyi $\delta > 0$ kadar genişleterek elde edilen $A_\delta$ kümesini tanımlayalım:

$A_\delta = \{x\in \mathbb{R}^2 : |x-y|<\delta, y\in A\}$

$A, B\subseteq \mathbb{R}^2$ için $B\subseteq A_\delta$ ve $A\subseteq B_\delta$ olacak şekilde bir $\delta$ elde etmeye, hatta bu özelliği sağlayan $\delta$ ‘ların en küçüğünü bulmaya çalışalım. (Kümeler kompakt olduğundan sınırlılar, dolayısıyla böyle bir $\delta$ ‘nın varlığından eminiz.) İşte elde ettiğimiz bu $\delta$ bize A ve B arasındaki Hausdorff uzaklığı verecektir. Şimdi yine aynı örnek üzerinden, bu metriği nasıl tanımlayabileceğimize bakalım.

İlk olarak, $A$ ‘nın $B$ ‘yi kapsayan bir genişlemesini yani, $B\subseteq A_{\delta_A}$ olacak şekilde bir $\delta_A$ bulmaya çalışalım. Bunun için, önce $A$ kümesinin her bir noktasının $B$ kümesine olan (en kısa) uzaklığını, yani $d(a,B)=inf_{b\in B} d(a,b)$ ‘yi buluruz. $A$ ‘nın $\delta_A$ genişlemesinin $B$ ‘yi kapsaması için ise bu uzaklıkların en büyüğünü seçeriz. Bu durumda $\delta_A= sup_{a\in A} d(a,B)$ olur.

Benzer şekilde, $\delta_B= sup_{b\in B} d(b,A)$ için $A\subseteq B_{\delta_B}$ olduğunu da görebiliriz. Fakat amacımız $A$ ve $B$ kümeleri için ortak bir $\delta$ elde etmek olduğundan

$\delta=\textrm{maks}\{\delta_A, \delta_B\}=\textrm{maks}\{ sup_{a\in A} d(a,B), sup_{b\in B} d(b,A) \}$

olarak seçeriz.

Hausdorff metriğinin en bilinen uygulamalarından biri, görüntü analizi, robotların görsel navigasyonu, bilgisayar destekli ameliyatlar gibi alanlarda kullanılan görüntü eşlemedir.

Yukarıdaki şekilde, solda verilen şablonun, sağdaki resimde olup olmadığını, varsa nerede olduğunu araştırırken Hausdorff metriği kullanılabilir. En iyi eşleşmeyi elde etmek için uzaklığın yeterince küçük olması gerekir.

Şimdi, asıl konumuza dönelim ve Hausdorff metriğin fraktal görüntü işleme alanında nasıl kullanıldığına bakalım.

Bir bilgisayarda görüntü depolarken karşılaşılan en temel sıkıntılardan biri depolama alanının kısıtlı olmasıdır. Görüntüyü depolarken, onu bir şekilde (sonlu bir) sıfırlar ve birler dizisine çevirmemiz gerekir. Bunu yapmak için görüntünün üzerine bir piksel ağı yerleştirdiğimizi ve bilgisayarın her pikselin değerini belleğine kaydettiğini düşünelim. Bir pikselin değeri, o noktadaki görüntünün siyah veya beyaz olmasına bağlı olarak 0 ya da 1 olsun. Bu yöntemde, görüntünün çözünürlüğü piksellerin büyüklüğüne bağlı olacaktır. Kullandığımız piksel sayısı depolama alanı ile sınırlıdır ve bu durum görüntünün netliğini ve ne kadar detaya sahip olup olmayacağını doğrudan etkiler. Bu sorunu çözmek fraktal sıkıştırma yöntemi kullanılabilir. Bunun için, işlemek istediğimiz görüntüye A diyelim ve $A_n=f(A_{n-1})$ ve $\lim A_n=A$ olacak şekilde bir $f$ prosesi bulmaya çalışalım. Hausdorff metriği işte tam burada devreye giriyor, çünkü $\lim A_n=A$ olması

$\forall \epsilon >0$ için, $\exists N\in \mathbb{N} ; n\geq N$ ise $H(A_n,A)<\epsilon$

koşulunun sağlanması anlamına gelir. (Burada H Hausdorff metriği gösterir.) Bu yöntem sayesinde, tüm görüntüyü depolamak yerine $f$ ‘yi depolamak yeterli olacaktır.

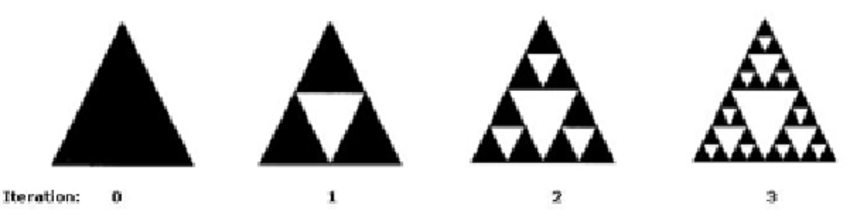
Yukarıda Sierpinski üçgeni ve onu elde etmek için kullanılan ilk üç iterasyonu görüyoruz. Bu üçgeni saklamak yerine, iterasyon kuralını saklamak tabii ki daha az yer kaplayacaktır.

Şimdi yukarıda anlatılanların matematiksel boyutuna bir bakalım.

$(X,d)$ bir tam metrik uzay olmak üzere, $\mathcal{H}(X)=\{A\subset X : A\neq \emptyset, A\hspace{0.1cm} \textrm{kompakt}\}$ kümesini tanımlayalım. Biliyoruz ki, $B\in \mathcal{H}(X)$ için $x$ ile $B$ kümesi arasındaki (en kısa) uzaklık $d(x,B)=\textrm{min} \{d(x,y) : y\in B\}$ biçiminde tanımlıdır. Burada B kümesi kompakt ve metrik fonksiyonu sürekli olduğundan minimum değerin varlığından söz edebiliriz. Çünkü kompakt bir küme üzerinde sürekli bir fonksiyonun maksimum ve minimum değerlerini aldığını biliyoruz.

Şimdi de $A, B\in \mathcal{H}(X)$ için $h(A,B)=\textrm{maks}\{d(x,B) : x\in A\}$ uzaklığını tanımlayalım. Dikkat edersek, h fonksiyonu $\mathcal{H}(X)$ üzerinde bir metrik değildir, çünkü simetri özelliğini sağlamaz. Örneğin, d standart metrik olmak üzere, $(\mathbb{R},d)$ tam metrik uzayında, $A=[3,4], B=[4,6]$ kompakt kümelerini düşünelim. $h(A,B)=1, h(B,A)=2$ olur, dolayısıyla $h(A,B)\neq h(B,A)$ ‘dir.

Teorem: $(X,d)$ bir tam metrik uzay ve $H: \mathcal{H}(X) \rightarrow \mathcal{H}(X)$ , $H(A,B)=\textrm{maks}\{h(A,B),h(B,A)\}$ olmak üzere $( \mathcal{H}(X) ,H)$ bir metrik uzaydır. (Bu metrik, $\mathcal{H}(X)$ üzerinde Hausdorff metriğidir.)

Bir görüntüyü $X=\mathbb{R}^2$ tam metrik uzayının kompakt bir alt kümesi olarak düşünebiliriz. Bu yaklaşımdan yola çıkarak, her bir görüntüyü $\mathcal{H}(X)$ uzayının bir noktası olarak kabul edip, bu uzayı “fraktallar uzayı” olarak adlandıralım.

Teorem: $(X,d)$ bir tam metrik uzay olsun. Bu durumda, $( \mathcal{H}(X) ,H)$ bir tam metrik uzaydır. Ayrıca $(A_n)$ , $\mathcal{H}(X)$ ‘de bir Cauchy dizisi olmak üzere, $\lim A_n=\{ x\in X : x_n \rightarrow x, x_n\in A_n, \hspace{0.1cm} \textrm{olacak \c{s}ekilde bir} \hspace{0.1cm} (x_n) \hspace{0.1cm} \textrm{Cauchy dizisi vard{\i}r.} \}$ biçiminde tanımlıdır.

Şimdi, $( \mathcal{H}(X) ,H)$ ‘in bir tam metrik uzay olmasından ve Banach sabit nokta teoreminden yararlanarak yakınsak bir dizi elde etmeye çalışalım. Bunun için önce daraltma dönüşümünün tanımını ve sabit nokta teoreminin ifadesini verelim.

Tanım: $(X,d)$ bir metrik uzay, $f:X\rightarrow X$ bir dönüşüm ve $0\leq s<1$ olsun. Eğer her $x,y\in X$ için $d(f(x),f(y))\leq s d(x,y)$ oluyorsa, $f$ ‘ye bir daraltma dönüşümü denir.

Teorem (Banach sabit nokta teoremi): $(X,d)$ bir tam metrik uzay ve $f:X\rightarrow X$ bir daraltma dönüşümü olsun. Bu durumda $f$ ‘nin tek bir sabit noktası vardır (Yani, $f(x_f)=x_f$ olacak şekilde tek bir $x_f\in X$ vardır). Ayrıca bu sabit nokta, her $x\in X$ için $f(x)=x, f^n(x)=(f\circ f^{n-1})(x)$ biçiminde elde edilen $(f^n(x))$ dizisinin limitidir, yani her $x\in X$ için $\lim f^n(x)=x_f$ ‘dir.

Demek ki, $( \mathcal{H}(X) ,H)$ üzerinde bir $f$ daraltma dönüşümü bulabilirsek, her $A\in \mathcal{H}(X)$ için, bu dönüşümün sabit noktasına yakınsayan bir $(f^n(A))$ dizisi de elde etmiş oluruz. Bu dönüşümü bulurken, X üzerinde tanımlı bir daraltma dönüşümlerinden yararlanabiliriz.

Lemma: $(X,d)$ bir tam metrik uzay olsun.
1) $w:X\rightarrow X$ sürekli bir fonksiyon ise, her $A\in \mathcal{H}(X)$ için $w(A)\in \mathcal{H}(X)$ olur.
2) $w:X\rightarrow X$ , $0\leq s<1$ faktörü ile bir daraltma dönüşümü ise, $w: \mathcal{H}(X) \rightarrow \mathcal{H}(X)$ , $\mathcal{H}(X)$ üzerinde $0\leq s <1$ faktörü ile bir daraltma dönüşümüdür, yani her $A,B\in \mathcal{H}(X)$ için $H(w(A),w(B))\leq s H(A,B)$ sağlanır.

Bu Lemma ile, X üzerinde tanımlı her daraltma dönüşümünün aynı zamanda $\mathcal{H}(X)$ üzerinde de bir daraltma dönüşümü olduğunu görmüş olduk. Şimdi $\mathcal{H}(X)$ üzerinde daha kapsamlı bir daraltma dönüşümü elde edeceğiz.

Lemma: $(X,d)$ bir tam metrik uzay ve her $n=1,2,\ldots N$ için $w_n$ , $s_n$ faktörüyle bir daraltma dönüşümü olsun. Bu durumda $W: \mathcal{H}(X) \rightarrow \mathcal{H}(X)$ , $W(B)=w_1(B)\cup w_2(B)\cup \ldots w_N(B)$ , $s=\textrm{maks}\{s_1, s_2,\ldots, s_N\}$ faktörü ile bir daraltma dönüşümüdür.

Tanım: $(X,d)$ bir tam metrik uzay ve her $n=1,2,\ldots N$ için $w_n$ , $s_n$ faktörüyle bir daraltma dönüşümü olmak üzere, $\{X; w_1,w_2,\ldots, w_N\}$ sistemine bir “Yinelemeli Fonksiyon Sistemi (Iterated Function System)” ya da kısaca bir IFS denir. Bu sistemin daraltma faktörü ise $s=\textrm{maks}\{s_1, s_2,\ldots, s_N\}$ ‘dir.

Eğer $W(B)=w_1(B)\cup w_2(B)\cup \ldots w_N(B)$ ise, yukarıdaki Lemma gereğince $W$ ‘nin $\mathcal{H}(X)$ üzerinde bir daraltma dönüşümü olduğunu söyleyebiliriz. O halde Banach Sabit Nokta Teoreminden, $W$ ‘nin tek bir $A\subset X$ sabit noktası ve her $B\in \mathcal{H}(X)$ için, $\lim W^n(B)=A$ olacak şekilde bir $(W^n(B))$ dizisi vardır. Burada $A$ kümesi, IFS’nin atraktörü olarak adlandırılır.

İşlemek istediğimiz bir görüntüyü, $\mathbb{R}^2$ ‘nin kompakt bir altkümesi olarak düşünebileceğimizden bahsetmiştik. Amacımız, $\mathbb{R}^2$ ‘de bir A görüntüsü verildiğinde, A’yı atraktör kabul eden bir IFS elde etmektir. Bu sayede, A görüntüsü yerine, içerisinde A’ya ulaşmak için gereken tüm bilgiler bulunan bir IFS’yi depolamış oluruz.

Şimdi bir $A\in \mathcal{H}(X)$ kümesi alalım ve her $B\in \mathcal{H}(X)$ için $c_A(B)=A$ olacak şekilde bir $c_A:\mathcal{H}(X) \rightarrow \mathcal{H}(X)$ dönüşümü tanımlayalım. Bu durumda her $B,D\in \mathcal{H}(X)$ için $H(c_A(B),c_A(D))=H(A,A)=0$ olduğundan $c_A$ bir daraltma dönüşümüdür ve dönüşümün tanımdan $c_A(A)=A$ ‘dir. O halde, $\{X,c_A\}$ , atraktörü $A$ olan bir IFS’dir. Tabii ki burada $c_A$ ‘yı depolamakla $A$ ‘yı depolamak aynı şey olduğundan, $c_A$ yeterince işe yarar bir dönüşüm değildir. Ama en azından verilen her $A$ görüntüsü için, atraktörü $A$ olan (iyi ya da kötü) bir IFS bulunabileceğini görmüş olduk.

Son olarak aşağıdaki teorem ile, her görüntü için daha basit, yani bir anlamda depolanması daha kolay olacak bir IFS bulmanın mümkün olduğu görelim.

Teorem (Kolaj Teoremi): $(X,d)$ bir tam metrik uzay olsun. $T\in \mathcal{H}(X)$ ve $\epsilon >0$ verilsin.

$H(T,\bigcup_{n=1}^N w_n(T))\leq \epsilon \hspace{3cm} (*)$

olacak şekilde, $0\leq s<1$ daraltma faktörüne sahip bir $\{X;w_1,w_2\ldots w_N\}$ seçelim. Bu durumda, $A$ bu IFS’nin atraktörü olmak üzere, $H(T;A)\leq \frac{\epsilon}{1-s}$ eşitsizliği sağlanır. Denk olarak, her $T\in \mathcal{H}(X)$ için

$H(T;A)\leq (1-s)^{-1} H(T, \bigcup_{n=1}^N w_n(T) )$ ‘dir.

Dolayısıyla, atraktörü, elimizdeki görüntüye yakın olan bir IFS bulmak için, yukarıdaki teoremde verilen (*) koşulunu sağlayan daraltma dönüşümleri bulmak gerekir. Bu teorem, belirli bir fraktal için bir IFS bulma problemini hemen çözmese de, probleme nasıl yaklaşılması gerektiği konusunda rehberlik eder.

Yukarıda kısaca anlattığımız, verilen bir görüntüyü, bir IFS ile temsil etme yöntemi “Fraktal Görüntü Sıkıştırma” olarak adlandırılır.

Son olarak, burada Kolaj Teoremi kullanılarak üretilmiş bir fraktal örneği bulabilirsiniz. Burada ise, Kolaj Teoreminin sahibi Michael Barnsley’in “Fractals Everywhere (Fraktallar Her Yerde)” adlı kitabında tanımladığı Barnsley Eğrelti otu isimli fraktalı elde etmek için kullanılan ve dört afin dönüşümden oluşan IFS’yi inceleyebilirsiniz.

Fraktallar her yerde olabilir, tamam, ama matematik de her yerdedir! 🙂

Kaynaklar
1)https://www.math.arizona.edu/~flaschka/Topmatter/527files/termpapers/mcmillen.pdf
2)https://www.youtube.com/watch?v=zGKfU91-hU0
3)http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/main.html

Topolojik bir oluşum!

Hausdorff Metriğinden Fraktal Görüntü Sıkıştırma Teknolojisine

Yorum bırakın Cevabı iptal et

Bunu paylaş:

İlgili

Yorum bırakın Cevabı iptal et